The Preliminary Contest for ICPC Asia Nanjing 2019

The Preliminary Contest for ICPC Asia Nanjing 2019

Holy Grail 

#include <bits/stdc++.h>

using namespace std;
const int maxn=10000;
int n,m;
struct Spfa {
    struct Edge {
        int next, to, w;
    } e[maxn];
    int head[maxn], v[maxn], d[maxn], tol;
 
    void add(int u, int v, int w) {
        tol++;
        e[tol].to = v;
        e[tol].next = head[u];
        e[tol].w = w;
        head[u] = tol;
    }
 
    queue<int> q;
 
    int spfa(int s, int t) {
        memset(d, 0x3f, sizeof(d));
        memset(v, 0, sizeof(v));
        d[s] = 0;
        v[s] = 1;
        q.push(s);
        while (!q.empty()) {
            int x = q.front();
            q.pop();
            v[x] = 0;
            for (int i = head[x]; i; i = e[i].next) {
                if (d[e[i].to] > d[x] + e[i].w) {
                    d[e[i].to] = d[x] + e[i].w;
                    if (v[e[i].to] == 0) {
                        v[e[i].to] = 1;
                        q.push(e[i].to);
                    }
                }
            }
        }
        return d[t] == 0x3f ? -1 : d[t];
    }
 
    void init() {
        memset(head, 0, sizeof(head));
        tol = 0;
    }
} S;
int main(){
    int _;
    scanf("%d",&_);
    while (_--){
        S.init();
        scanf("%d%d",&n,&m);
        for (int i=1,u,v,w;i<=m;i++){
            scanf("%d%d%d",&u,&v,&w);
            S.add(u,v,w);
        }
        for (int i=1,u,v;i<=6;i++){
            scanf("%d%d",&u,&v);
            int ans=S.spfa(v,u);
            printf("%d
",-ans);
            S.add(u,v,-ans);
        }
    }
}

Greedy Sequence

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+50;
struct CT{
#define mid (l+r)/2
    int tot,sum[N*30],ls[N*30],rs[N*30];
    void init(){
        tot=0;
    }
    int build(int l,int r){
        int rt=++tot;
        sum[rt]=ls[rt]=rs[rt]=0;
        if(l<r){
            ls[rt]=build(l,mid);
            rs[rt]=build(mid+1,r);
        }
        return rt;
    }
    int update(int pre,int l,int r,int x){
        int rt=++tot;
        ls[rt]=ls[pre];
        rs[rt]=rs[pre];
        sum[rt]=sum[pre]+1;
        if(l<r){
            if(x<=mid){
                ls[rt]=update(ls[pre],l,mid,x);
            }else{
                rs[rt]=update(rs[pre],mid+1,r,x);
            }
        }
        return rt;
    }
    int query(int u,int v,int l,int r,int k){
        if(l>=r){
            if(l<k && sum[v]-sum[u]){
                return l;
            }else{
                return 0;
            }
        }
        if(k<=mid+1 || sum[rs[v]]-sum[rs[u]]==0){
            return query(ls[u],ls[v],l,mid,k);
        }
        int t=query(rs[u],rs[v],mid+1,r,k);
        if(t){
            return t;
        }else{
            return query(ls[u],ls[v],l,mid,k);
        }
    }
    void debug(int rt,int l,int r){
        printf("%d %d %d
",l,r,sum[rt]);
        if(l==r){
            return;
        }
        debug(ls[rt],l,mid);
        debug(rs[rt],mid+1,r);
    }
}ac;
int tr[N];
int T,n,k,a[N],p[N],ans[N];
int main(){
//    freopen("in.txt","r",stdin);
    scanf("%d",&T);
    while(T--){
        scanf("%d%d",&n,&k);
        for(int i=1;i<=n;i++){
            scanf("%d",&a[i]);
            p[a[i]]=i;
        }
        ac.init();
        tr[0]=ac.build(1,n);
        for(int i=1;i<=n;i++){
            tr[i]=ac.update(tr[i-1],1,n,a[i]);
        }
        ans[1]=1;
        for(int i=2;i<=n;i++){
            int L=max(1,p[i]-k);
            int R=min(n,p[i]+k);
            int x=ac.query(tr[L-1],tr[R],1,n,i);
            ans[i]=ans[x]+1;
        }
        for(int i=1;i<=n;i++){
            printf("%d%c",ans[i],i==n?'
':' ');
        }
    }
    return 0;
}

　　

#include <bits/stdc++.h>

using namespace std;
const int maxn=1e5+10;
int tot,t[maxn*30],ans[maxn],L[maxn*30],R[maxn*30],a[maxn],b[maxn],n,c[maxn],k;
vector<int>root;
int build(int l,int r) {
    int id = ++tot;
    t[id] = 0;
    if (l == r) return id;
    int mid = (l + r) >> 1;
    L[id] = build(l, mid);
    R[id] = build(mid + 1, r);
    return id;
}

void insert1(int id1,int x) {
    int id2 = ++tot;
    root.push_back(id2);
    t[id2] = t[id1] + 1;
    int l = 1, r = n;
    while (l < r) {
        int mid = (l + r) >> 1;
        if (x <= mid) {
            r = mid;
            L[id2] = ++tot;
            R[id2] = R[id1];
            id2 = tot;
            id1 = L[id1];
        } else {
            l = mid + 1;
            R[id2] = ++tot;
            L[id2] = L[id1];
            id2 = tot;
            id1 = R[id1];
        }
        t[id2] = t[id1] + 1;
    }
}
int query1(int id,int l,int r,int x) {
    if (x >= a[r]) return t[id];
    else if (x < a[l]) return 0;
    int res = 0;
    int mid = (l + r) >> 1;
    if (x <= a[mid]) res = query1(L[id], l, mid, x);
    else {
        res += t[L[id]];
        res += query1(R[id], mid + 1, r, x);
    }
    return res;
}
int query(int l,int r,int LL,int RR,int k)
{
    if (l==r)
        return l;
    int mid=(l+r)>>1;
    int tmp=t[L[RR]]-t[L[LL]];
    if (k<=tmp)
    {
        return query(l,mid,L[LL],L[RR],k);
    }
    else
    {
        return query(mid+1,r,R[LL],R[RR],k-tmp);
    }
}
int main() {
    int _;
    scanf("%d", &_);
    while (_--) {
        tot =  0;
        scanf("%d%d", &n, &k);
        root.clear();
        for (int i = 1; i <= n; i++) {
            ans[i]=0;
            scanf("%d", &b[i]);
            a[i] = b[i];
            c[a[i]] = i;
        }
        sort(a + 1, a + 1 + n);
        n = unique(a + 1, a + n + 1) - (a + 1);
        root.push_back(build(1, n));
        for (int i = 1; i <= n; i++) {
            insert1(root[i - 1],b[i]);
        }
        for (int i = 1; i <= n; i++) {
            int id = c[i];
            while (1) {
                ans[i]++;
                int kk = query1(root[min(n, id + k)], 1, n, b[id]) - query1(root[max(1, id - k) - 1], 1, n, b[id]) - 1;
                if (kk == 0) break;
                id = c[a[query(1, n, root[max(1, id - k) - 1], root[min(n, id + k)], kk)]];
                if (ans[b[id]]) {
                    ans[i] += ans[b[id]];
                    break;
                }
            }
        }
        for (int i = 1; i <= n; i++) {
            if (i != n) printf("%d ", ans[i]); else printf("%d
", ans[i]);
        }
    }
    return 0;
}

The beautiful values of the palace

 

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
const int maxn=1e6+10;
int n,m,p,tot;
ll ans[maxn],d[maxn];
struct node {
    int x, y, id, flag;

    node(int _x = 0, int _y = 0, int _id = 0, int _flag = 0) : x(_x), y(_y), id(_id), flag(_flag) {};

    bool operator<(const node &b) const {
        return y < b.y;
    }
}q[maxn*4];

struct node1 {
    int x, y, val;

    node1(int _x = 0, int _y = 0, int _val = 0) : x(_x), y(_y), val(_val) {};

    bool operator<(const node1 &b) const {
        return y < b.y;
    }
}a[maxn];

ll c[maxn*2];

int lowbit(int x){
    return x&-x;
}

void add(int x,ll val){
    if (x==0) return;
    while (x<maxn){
        c[x]+=val;
        x+=lowbit(x);
    }
}

ll query(int x) {
    ll ret = 0;
    while (x) {
        ret += c[x];
        x -= lowbit(x);
    }
    return ret;
}

void solve() {
    int pos = 1;
    for (int i = 1; i <= tot; i++) {
        while (pos <= m && a[pos].y <= q[i].y) {
            add(a[pos].x, a[pos].val);
            pos++;
        }
        ans[q[i].id] += query(q[i].x) * q[i].flag;
    }
}

ll sum(ll x) {
    ll ret = 0;
    while (x) {
        ret += x % 10;
        x /= 10;
    }
    return ret;
}

ll get(ll x,ll y,ll n) {
    int cx = n / 2 + 1;
    int cy = n / 2 + 1;
    ll k = max(abs(x - cx), abs(y - cy));
    if (k == 0) return n * n;
    ll res = d[k - 1];
    if (y - cy == k && x < cx + k)
        res += cx + k - x;
    else if (cx - x == k && y < cy + k)
        res += k * 2 + cy + k - y;
    else if (cy - y == k && x > cx - k)
        res += k * 4 + x + k - cx;
    else if (x - cx == k) res += k * 6 + y - cy + k;
    res = n * n - res;
    return res+1;
}

int main() {
    int _;
    d[0]=1;d[1]=8;
    for (int i=2;i<=maxn;i++) d[i]=d[i-1]+8;
    for (int i=1;i<=maxn;i++) d[i]+=d[i-1];
    scanf("%d", &_);
    while (_--) {
        scanf("%d%d%d", &n, &m, &p);
        for (int i = 0; i <= 2 * n; i++) c[i] = 0;
        for (int i = 0; i <= p; i++) ans[i] = 0;
        for (int i = 1, x, y; i <= m; i++) {
            scanf("%d%d", &x, &y);
            a[i] = node1(x, y, sum(get(x, y, n)));
        }
        tot = 0;
        sort(a + 1, a + m + 1);
        for (int i = 1, x1, yy, x2, y2; i <= p; i++) {
            scanf("%d%d%d%d", &x1, &yy, &x2, &y2);
            q[++tot] = node(x1 - 1, yy - 1, i, 1);
            q[++tot] = node(x1 - 1, y2, i, -1);
            q[++tot] = node(x2, yy - 1, i, -1);
            q[++tot] = node(x2, y2, i, 1);
        }
        sort(q + 1, q + tot + 1);
        solve();
        for (int i = 1; i <= p; i++) {
            printf("%lld
", max(0ll, ans[i]));
        }
    }
    return 0;
}

super_log

所给的函数是一个递归的形式，每递归一次就是+1，容易推出最后X = ((a^a)^a)^a......【b个a的幂】，算是一个原题【BZOJ-3884】(简单版)，【CF-906D】(加强版)，实现就是欧拉广义降幂的递归形式，注意b=0时输出(1 mod m)

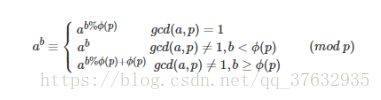
#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
ll a,b,mod;

ll eular(ll n) {
    ll phi = n;
    for (ll i = 2; i * i <= n; i++) {
        if (n % i == 0) {
            phi = phi * (i - 1) / i;
            while (n % i == 0) n = n / i;
        }
    }
    if (n > 1) phi = phi * (n - 1) / n;
    return phi;
}

ll pow_mod(ll a,ll x,ll mod) {
    ll res = 1;
    while (x) {
        if (x & 1) res = res * a % mod;
        a = a * a % mod;
        x = x >> 1;
    }
    return res;
}
ll solve(ll a,ll b,ll mod) {
    if (mod==1)
        return 0;
    if (b==0)
        return 1;
    ll phi = eular(mod);
    ll p = solve(a, b-1, phi);
    if (p < phi && p) return pow_mod(a, p, mod); else return pow_mod(a, p + phi, mod);
}

int main() {
    int _;
    scanf("%d", &_);
    while (_--) {
        scanf("%d%d%d", &a, &b, &mod);
        if (b == 0) {
            printf("%d
", 1 % mod);
        } else {
            printf("%d
", solve(a, b, mod) % mod);
        }
    }
    return 0;
}