题面:

数据范围:
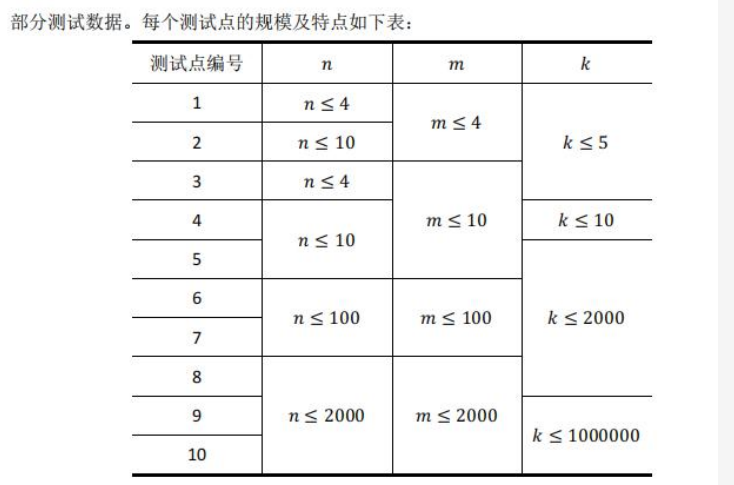
Solution
小(trick)+斯特林数+组合数
首先我们观察一下样例:
可以发现除开第一列和最后一列,其它的所以处于这中间的列每列拥有的不同种类的颜色必须一模一样
即:
假设现在有这样的中间两列(x)和(y)
如果(x)列的颜色集合为(x_i),(i=1,2,3,4...n),则(y)列的颜色集合(y_i)也必须和其完全相同
证明:
反证:若当前分割线处在第(i-1)列和第(i)列之间满足题意的性质,且第(i)列和第(i+1)列有不同的颜色,此时我们要把分割线移动到第(i)列到第(i+1)列之间,若可行则上述结论不成立,若不行则上述结论成立
假设(1)$i-1$列拥有$x$种颜色,那么$i$(n)列就也拥有(x)种颜色
而当第(i)列和第(i+1)列不同时,假设有(c)种不同的颜色,那么此时前(i)列就有(x+c)种颜色,而第(i+1)-(n)列显然拥有的颜色数量比第(i)-(n)列拥有的要少或者相同(因为少了一列嘛)
而此时这条分割线就不满足题意了,则假设不成立
所以证得:如果(x)列的颜色集合为(x_i),(i=1,2,3,4...n),则(y)列的颜色集合(y_i)也必须和其完全相同
而且,如果我们要满足题面的性质的话,还需要的一个条件是:第(1)列和第(n)列的颜色数量必须相同
现在我们就获得了两个对于这个性质的充要条件,可以开始计数了
接下来我们相当于只需要枚举第一列可能的颜色种数和最后一列的和中间选择的颜色即可
可以写出公式:
(C(k,i)*i^{(m-2)*n}*C(k-i,j)*C(k-i-j,j)*(S(i+j,n)*(i+j)!)^2)
此时这里的(C)是组合数,(S)是第二类斯特林数
我们逐项解释:
(i)表示中间列的颜色种数
(C(k,i))先从(k)种颜色当中选(i)个颜色填到中间,
(i^{(m-2)*n})即中间的每一个格子都有(i)种选择,共((m-2)*n)种选择
(C(k-i,j))从剩下的(k-i)个数当中选择(j)个数填到第一列当中
(C(k-i-j,j))再从剩下的(k-i-j)个数当中选择(j)个填到最后一列当中
(S(i+j,n))就是在(i+j)个格子当中填(n)个物品且每个格子至少填一个物品,的方案数
((i+j)!)因为第二类斯特林数本身的定义中这(i+j)个格子是无序的,但是我们这里是有序的,所以乘上全排列就行了
((S(i+j,n)*(i+j)!)^2)这里的平方因为第一列和最后一列都要这样填,所以是平方
第二类斯特林数的递推公式稍微(dp)一下就可以了
设:(S(i,j))表示在(i)个箱子里放(j)个球,每个箱子至少放一个的方案数(箱子无序)
那么显然可以得到:(S[i][j]=S[i-1][j-1]+S[i-1][j]*j)
即:当前这个球可以选择放入一个新的盒子或者和之前已有的(j)个盒子中的某一个合并
组合数递推式就懒得写了,不会的自己去康康...其实这里直接通项公式也行...稍微注意一下逆元就行了...