题意
复述一下题意:
给定一个有向图,保证图连通,要求取出其中(x)个点作为集合(G),使得(G)内部的所有点之间没有直接相连的边
且图上的任何一个点都满足:从集合(G)内的某个点出发,在两步之内到达(经过一条边即走了一步)
简而言之就是两条:
(1.)分隔性(不直接相连)
(2.)可达性(两步之内到达任意点)
思路
我们可以考虑构造一个这样的方案:
对于一个图,我们每次隔一层来选点(一层指(BFS)遍历中的遍历层数)
比如这样:
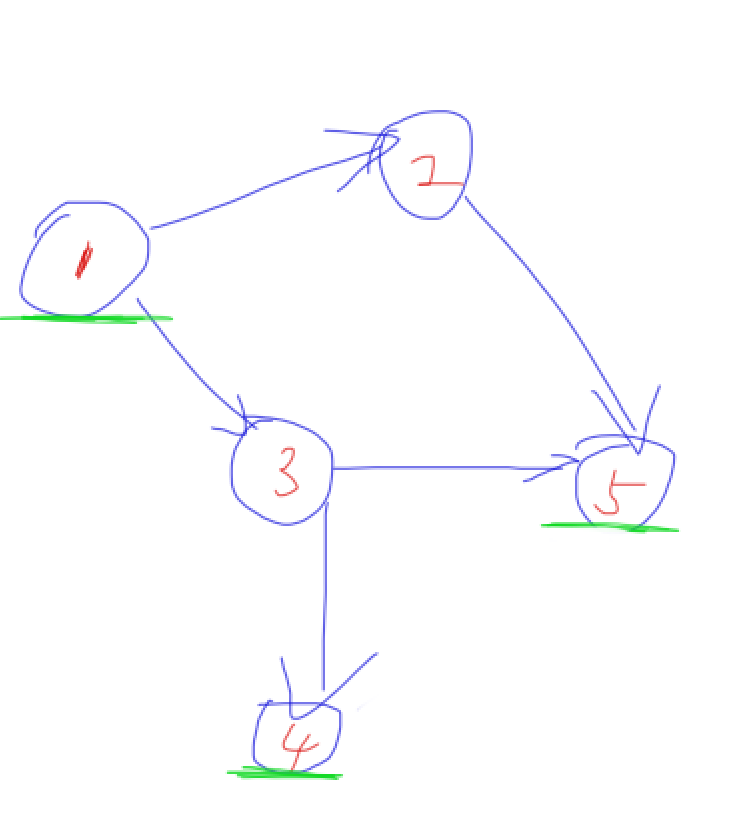
其中我们从(1)结点开始(第一层),那么(2,3)就是第二层,(4,5)是第三层
那么我们就选第一层和第三层(即选奇数层)
(Q1:)想一想,我们这样选保证了什么(?)
(A1:)保证了可达性
即这样选,绝对不会造成某个点我们两步之内到不了的情况(其实因为我们是隔一层选一个,这个条件在这里更是被加强到了一步之内可以到达任意结点)
于是我们现在就可以考虑一下这样来选,那么现在的问题是:
我们这样做可以保证可达性,但是分隔性呢?
我们能够确保一定不会同时选到两个同一层的点吗?(换而言之,我们这样会把所以处于奇数层的点都选了,但是其实在这一层中的两个点也是有可能有连边的)
答案是显然不能,比如我们在刚刚图的基础上,加一条(5-4)的边:
现在我们还是会选到(1,4,5)三个点,因为此时(1)在第一层,(4,5)都在第三层,我们要选奇数层的,所以我们现在会选到(1,4,5)
但是,这样选对吗?
不对。
因为我们发现,此时有了边((5,4)),这会导致(4,5)两个点不能同时选,最多只能选一个(因为(G)集合内的点不能直接相连)
那么我们现在知道,刚刚我们设计的构造方法是不正确的,它只保证了可达性,却不能保证分隔性。
于是我们可以考虑优化刚刚的做法,去除掉两个相邻点中的某一个以保证分隔性
为什么是去掉两个中的某一个呢?
因为我们刚刚也提到了,我们之前的这种构造办法会加强我们可达性的条件,从两步变成一步,而我们把不满足分隔性的某一对点中的一个点删掉(即不选这个点)。
这样做会产生的影响就是导致由这个点所约束的周围一圈点可能会不满足可达性了
约束指的是,因为在之前我们每个点都能一步到达其周围一圈的点,让这一圈的点都不会影响到可达性,因为我们此时集合内已经有了点可以一步到达这一圈点中的任意一个
于是我们删掉(G)集合内的一个点(假设点编号为(x))产生的影响就是这样:原本被(x)约束着的所有点(y)(即(y in son_x))有可能现在就不能在两步之内到达了。
但是,其实这样删(指如果出现两个同层且有连边的点)是没有影响的。
接下来我们就来证明这个结论:
不妨设两个点的编号分别是(x,y)且(xleq y),假设这条边是((y,x)),即从(y)指向(x)
那么现在我们就删掉(x),因为此时我们知道:
(1.y)可以一步到达(x) (quad) [有边((y,x))]
(2.)删掉(x)之后会有影响的只是(x)周围一圈的点(即(x)可以一步到达的所有点)
那么因为(y-x)需要一步,(x-)有影响的点 需要一步,则 (y-)有影响的点 需要两步
而题目要求的可达性也就是两步之内要能够到达
于是我们便感性证明了,在这种情况下删掉(x),对答案的可达性没有影响,而我们删掉(x)的这个操作,又会保证答案的分隔性,那么这不就两个条件都满足了(?)
问题也就解决了。
实现
那么现在考虑怎么实现。
定义两个(bool)标记,一个(sel)表示当前点被选没有,一个(vis)表示当前点被访问过没有
首先我们从(1-n)枚举每个点,每次先判断当前点被访问过没有,如果有就直接跳过,如果没有,我们就可以把(vis)标记为访问过,然后把(sel)标记为(true),把当前这个点选进集合,然后遍历这个点的所有出边,把周围一圈的点(即一部就可以到达的点)的(vis)设为访问过了
接下来是删除的过程:
我们从(n-1)枚举每个点,然后每次看当前点被选没有,如果没有直接跳过,如果有,那么把这个点周围的一圈(sel)标记设为(false),即删除当前这个点周围的所有之前被选入集合的点(因为当前这个点既然要选就必须得删掉和它相邻的又被选了的)
最后当前(sel)标记为(true)的就是要选的答案集合中的元素,即答案
现在考虑这样做的正确性:
在第一个循环中,我们从小到大枚举更新,
一是保证了可行性:每个点只会被周围一圈的点限制,没有被限制的都被选入集合了
二是保证了最后会影响到答案的一对点一定是 编号大(-)编号小(即编号大的点指向编号小的点),因为如果是编号小(-)编号大的边,我们一定会在遍历到编号小的点的时候就直接把编号大的点给叉掉了(因为我们要叉掉周围一圈嘛),此时大的就根本不会被选,也就更没有删掉一说了
在第二个循环中,我们从大到小枚举,这就能保证:只会是大的点叉掉小的点,即大的点会被保留,删掉小的点,为什么保留大点删掉小点呢?因为之前我们不是说了要删掉被指向的那个点吗,之前第一个循环又保证了一定是编号大的点指向编号小的点,所以被指着的一定是编号小的,这才要倒着删,这样删的话大的只会删掉小的,而小的无法删掉大的(因为如果可以那这个小的早就被大点率先删掉了)
那么最后统计一遍答案就行了
代码
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T,typename... Args> inline void read(T& t, Args&... args){read(t);read(args...);}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
template <typename T>
inline void print(T x){write(x),putchar(' ');}
#define ll long long
#define ull unsigned long long
#define inc(x,y) (x+y>=MOD?x+y-MOD:x+y)
#define dec(x,y) (x-y<0?x-y+MOD:x-y)
#define min(x,y) (x<y?x:y)
#define max(x,y) (x>y?x:y)
const int N=1e6+5,M=1e6+5,MOD=1e9+7;
int n,m;
int head[N],nex[M],to[M],idx;
bool vis[N],f[N];
void add(int u,int v){
nex[++idx]=head[u];
to[idx]=v;
head[u]=idx;
return ;
}
int main(){
read(n);read(m);
for(int i=1;i<=m;i++){
int u,v;
read(u,v);
add(u,v);
}
for(int i=1;i<=n;i++){
if(!vis[i]){
vis[i]=true;
f[i]=true;
for(int j=head[i];j;j=nex[j]){
int y=to[j];
vis[y]=true;
}
}
}
for(int i=n;i>=1;i--){
if(vis[i]){
if(f[i]){
for(int j=head[i];j;j=nex[j]){
int y=to[j];
f[y]=false;
}
}
}
}
int ans=0;
for(int i=1;i<=n;i++) if(f[i]) ans++;
write(ans);putchar('
');
for(int i=1;i<=n;i++) if(f[i]) write(i),putchar(' ');
return 0;
}
``