题目
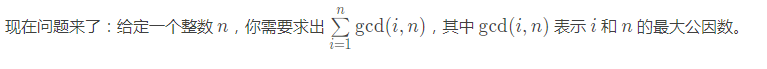

分析
根据欧拉函数性质7推论3
(Large sumlimits_{i=1}^{n}{(i,n)}=sumlimits_{i=1}^{n}{sumlimits_{d|i}{sumlimits_{d|n}{varphi{(d)}}}}=sumlimits_{d|n}{sumlimits_{i=1}^{n}{sumlimits_{d|i}{varphi{(d)}}}}=sumlimits_{d|n}{varphi{(d)}lfloordfrac{n}{d} floor})
于是可以得到这个柿子,显然可以整除分块,欧拉函数使用计算式直接算即可。
代码
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x){
x=0;char ch=getchar();bool f=false;
while(!isdigit(ch)){if(ch=='-'){f=true;}ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return ;
}
template <typename T>
inline void write(T x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10^48);
return ;
}
const int N=1e6+5,M=1e6+5,MOD=10000;
#define ll long long
ll n;
#define ll long long
#define ull unsigned long long
#define ld long double
inline ll mul(ll x,ll y,ll mod){
ll res=x*y-mod*(ll)((ld)x/mod*y);
if(res<0)return res+mod;
if(res<mod)return res;
return res-mod;
}
ll QuickPow(ll x,ll y,ll mod){
ll res=1;
for(;y;y>>=1,x=mul(x,x,mod)) if(y&1) res=mul(res,x,mod);
return res;
}
ll test[3]={2,61};
inline bool Miller_Rabin(ll x){
if(x==1) return false;
ll t=x-1,k=0;
while(!(t&1)) t>>=1,k++;
for(int i=0;i<2;i++){
if(x==test[i]) return true;
ll a=QuickPow(test[i],t,x),Nex=a;
for(int j=1;j<=k;j++){
Nex=mul(a,a,x);
if(Nex==1&&a!=1&&a!=x-1) return false;
a=Nex;
}
if(a!=1) return false;
}
return true;
}
inline bool prime(ll x){
if(x==46856248255981ll||x<2)return false;
if(x==2||x==3||x==7||x==61||x==24251) return true;
return Miller_Rabin(x);
}
ll gcd(ll x,ll y){return y?gcd(y,x%y):x;}
inline ll f(ll x,ll c,ll mod){
ll res=mul(x,x,mod)+c;
return res<mod?res:res-mod;
}
inline ll Pollard_Rho(ll x){
ll c=rand()%(x-1),s=0;
for(ll lim=1;;lim<<=1){
ll t=s,now=1;
for(ll j=1;j<=lim;j++){
s=f(s,c,x);
now=mul(now,abs(s-t),x);
if(!now){ll d=gcd(s,x);if(d>1)return d;return x;}
if(j%127==0){ll d=gcd(now,x);if(d>1)return d;}
}
ll d=gcd(s,x);
if(d>1) return d;
}
}
ll Maxn;
map<ll,int>fac;
inline void GetFact(ll x){
if(x<=1) return ;
if(prime(x)){
fac[x]++;
return ;
}
ll p=Pollard_Rho(x);
while(p>=x) p=Pollard_Rho(x);
GetFact(x/p),GetFact(p);
return ;
}
inline ll GetPhi(ll x){
map<ll,int>Map;
swap(Map,fac);
GetFact(x);
for(map<ll,int>::iterator it=fac.begin();it!=fac.end();it++) x=x/(*it).first*((*it).first-1);
return x;
}
int main(){
read(n);ll Ans=0,p;
for(ll k=1;k*k<=n;k++){
if(n%k==0){
p=k;
Ans+=GetPhi(p)*(n/p);
p=n/k;
if(k==p) continue;
Ans+=GetPhi(p)*(n/p);
}
}
write(Ans);
return 0;
}
扩展
可以注意到这个函数也可以直接线性筛出来。