本书到目前为止都是在讨论TopN推荐,即给定一个用户,如何给他生成一个长度为N的推荐列表,使该推荐列表能够尽量满足用户的兴趣和需求。
本书之所以如此重视TopN推荐,是因为它非常接近于满足实际系统的需求,实际系统绝大多数情况下就是给用户提供一个包括N个物品的个性化推荐列表。
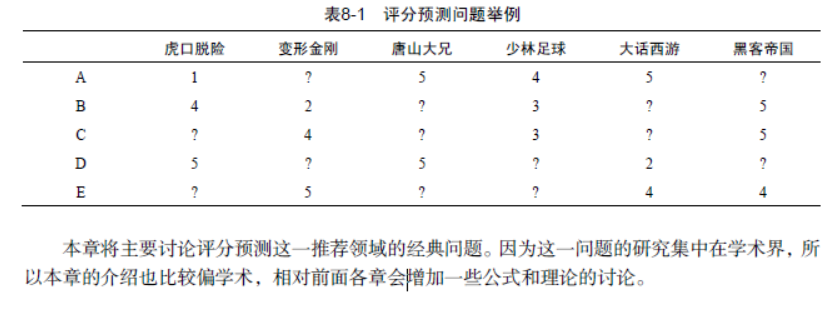
评分预测问题最基本的数据集就是用户评分数据集。该数据集由用户评分记录组成,每一条评分记录是一个三元组(u,i, r),表示用户u给物品i赋予了评分r,本章用ui r 表示用户u对物品i的评分。
因为用户不可能对所有物品都评分,因此评分预测问题就是如何通过已知的用户历史评分记录预测未知的用户评分记录。
1、离线实验方法

关于如何划分训练集和测试集,如果是和时间无关的预测任务,可以以均匀分布随机划分数据集,即对每个用户,随机选择一些评分记录作为测试集,剩下的记录作为测试集。如果是和时间相关的任务,那么需要将用户的旧行为作为训练集,将用户的新行为作为测试集。Netflix通过如下方式划分数据集,首先将每个用户的评分记录按照从早到晚进行排序,然后将用户最后10%的评分记录作为测试集,前90%的评分记录作为训练集。
2、评分预测算法
1) 平均值
最简单的评分预测算法是利用平均值预测用户对物品的评分的。下面各节将分别介绍各种不同的平均值。
1. 全局平均值
2. 用户评分平均值
3. 物品评分平均值
4.用户分类对物品分类的平均值
用户和物品的平均分 对于一个用户,可以计算他的评分平均分。然后将所有用户按照评分平均分从小到大排序,并将用户按照平均分平均分成N类。物品也可以用同样的方式分类。
用户活跃度和物品流行度 对于一个用户,将他评分的物品数量定义为他的活跃度。得到用户活跃度之后,可以将用户通过活跃度从小到大排序,然后平均分为N类。物品的流行度定义为给物品评分的用户数目,物品也可以按照流行度均匀分成N类。
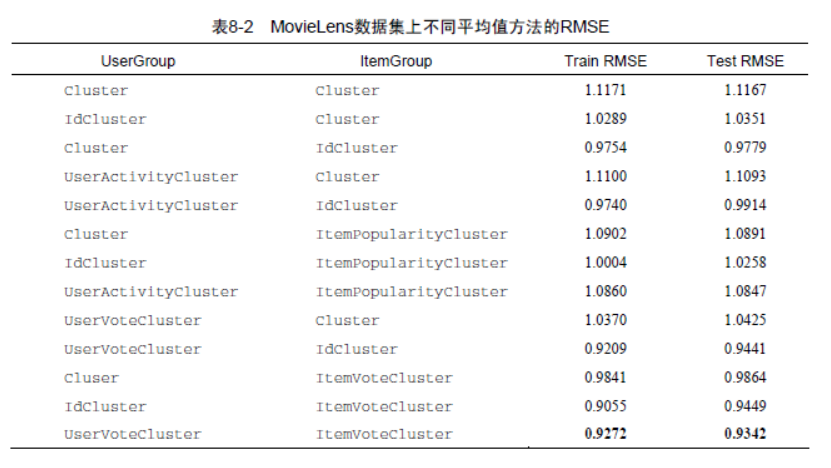
MovieLens数据集中利用不同平均值方法得到的RMSE,实验结果表明对用户使用UserVoteCluster,对物品采用ItemVoteCluster,可以获得最小的RMSE。
2) 基于邻域的方法



3) 隐语义模型与矩阵分解模型
最近这几年做机器学习和数据挖掘研究的人经常会看到下面的各种名词,即隐含类别模型(Latent Class Model)、隐语义模型(Latent Factor Model)、pLSA、LDA、Topic Model、MatrixFactorization、Factorized Model。
这些名词在本质上应该是同一种思想体系的不同扩展。在推荐系统领域,提的最多的就是潜语义模型和矩阵分解模型。其实,这两个名词说的是一回事,就是如何通过降维的方法将评分矩阵补全。
用户的评分行为可以表示成一个评分矩阵R,其中R[u][i]就是用户u对物品i的评分。但是,用户不会对所有的物品评分,所以这个矩阵里有很多元素都是空的,这些空的元素称为缺失值(missing value)。因此,评分预测从某种意义上说就是填空,如果一个用户对一个物品没有评过分,那么推荐系统就要预测这个用户是否是否会对这个物品评分以及会评几分。
1. 传统的SVD分解
对于如何补全一个矩阵,历史上有过很多的研究。一个空的矩阵有很多种补全方法,而我们要找的是一种对矩阵扰动最小的补全方法。那么什么才算是对矩阵扰动最小呢?一般认为,如果补全后矩阵的特征值和补全之前矩阵的特征值相差不大,就算是扰动比较小。所以,最早的矩阵分解模型就是从数学上的SVD(奇异值分解)开始的。②给定m个用户和n个物品,和用户对物品

SVD分解是早期推荐系统研究常用的矩阵分解方法,不过该方法具有以下缺点,因此很难在实际系统中应用。
该方法首先需要用一个简单的方法补全稀疏评分矩阵。一般来说,推荐系统中的评分矩阵是非常稀疏的,一般都有95%以上的元素是缺失的。而一旦补全,评分矩阵就会变成一个稠密矩阵,从而使评分矩阵的存储需要非常大的空间,这种空间的需求在实际系统中是不可能接受的。
该方法依赖的SVD分解方法的计算复杂度很高,特别是在稠密的大规模矩阵上更是非常慢。一般来说,这里的SVD分解用于1000维以上的矩阵就已经非常慢了,而实际系统动辄是上千万的用户和几百万的物品,所以这一方法无法使用。如果仔细研究关于这一方法的论文可以发现,实验都是在几百个用户、几百个物品的数据集上进行的。
2. Simon Funk的SVD分解


3. 加入偏置项后的LFM


4. 考虑邻域影响的LFM
前面的LFM模型中并没有显式地考虑用户的历史行为对用户评分预测的影响。为此,Koren在Netflix Prize比赛中提出了一个模型①,将用户历史评分的物品加入到了LFM模型中,Koren将该模型称为SVD++。
在介绍SVD++之前,我们首先讨论一下如何将基于邻域的方法也像LFM那样设计成一个可以学习的模型。其实很简单,我们可以将ItemCF的预测算法改成如下方式:

4) 加入时间信息

2. 基于矩阵分解的模型融合时间信息
在引入时间信息后,用户评分矩阵不再是一个二维矩阵,而是变成了一个三维矩阵。不过

5) 模型融合
Netflix Prize的最终获胜队伍通过融合上百个模型的结果才取得了最终的成功。由此可见模型融合对提高评分预测的精度至关重要。本节讨论模型融合的两种不同技术。
1. 模型级联融合
级联融合很像Adaboost算法。和Adaboost算法类似,该方法每次产生一个新模型,按照一定的参数加到旧模型上去,从而使训练集误差最小化。不同的是,这里每次生成新模型时并不对样本集采样,针对那些预测错的样本,而是每次都还是利用全样本集进行预测,但每次使用的模型都有区别。一般来说,级联融合的方法都用于简单的预测器,比如前面提到的平均值预测器。
2. 模型加权融合
假设我们有K个不同的预测器{r(1) , r(2) , ..., r(K )},本节主要讨论如何将它们融合起来获得最低的预测误差。
最简单的融合算法就是线性融合,即最终的预测器ˆr 是这K个预测器的线性加权。
一般来说,评分预测问题的解决需要在训练集上训练K个不同的预测器,然后在测试集上作出预测。但是,如果我们继续在训练集上融合K个预测器,得到线性加权系数,就会造成过拟合的问题。
因此,在模型融合时一般采用如下方法:
假设数据集已经被分为了训练集A和测试集B,那么首先需要将训练集A按照相同的分割方法分为A1和A2,其中A2的生成方法和B的生成方法一致,且大小相似。
在A1上训练K个不同的预测器,在A2上作出预测。因为我们知道A2上的真实评分值,所以可以在A2上利用最小二乘法①计算出线性融合系数k。
在A上训练K个不同的预测器,在B上作出预测,并且将这K个预测器在B上的预测结果按照已经得到的线性融合系数加权融合,以得到最终的预测结果。
除了线性融合,还有很多复杂的融合方法,比如利用人工神经网络的融合算法。其实,模型融合问题就是一个典型的回归问题,因此所有的回归算法都可以用于模型融合。

总结
最后,我想引用2009年ACM推荐系统大会上Strand研究人员做的一个报告“推荐系统十堂课”,在这个报告中Strand的研究人员总结了他们设计推荐系统的经验,提出了10条在设计推荐系统中学习到的经验和教训。
(1) 确定你真的需要推荐系统。推荐系统只有在用户遇到信息过载时才必要。如果你的网站物品不太多,或者用户兴趣都比较单一,那么也许并不需要推荐系统。所以不要纠结于推荐系统这个词,不要为了做推荐系统而做推荐系统,而是应该从用户的角度出发,设计出能够真正帮助用户发现内容的系统,无论这个系统算法是否复杂,只要能够真正帮助用户,就是一个好的系统。
(2) 确定商业目标和用户满意度之间的关系。对用户好的推荐系统不代表商业上有用的推荐系统,因此要首先确定用户满意的推荐系统和商业上需求的差距。一般来说,有些时候用户满意和商业需求并不吻合。但是一般情况下,用户满意度总是符合企业的长期利益,因此这一条的主要观点是要平衡企业的长期利益和短期利益之间的关系。
(3) 选择合适的开发人员。一般来说,如果是一家大公司,应该雇用自己的开发人员来专门进行推荐系统的开发。
(4) 忘记冷启动的问题。不断地创新,互联网上有任何你想要的数据。只要用户喜欢你的产品,他们就会不断贡献新的数据。
(5) 平衡数据和算法之间的关系。使用正确的用户数据对推荐系统至关重要。对用户行为数据的深刻理解是设计好推荐系统的必要条件,因此分析数据是设计系统中最重要的部分。数据分析决定了如何设计模型,而算法只是决定了最终如何优化模型。
(6) 找到相关的物品很容易,但是何时以何种方式将它们展现给用户是很困难的。不要为了推荐而推荐.
(7) 不要浪费时间计算相似兴趣的用户,可以直接利用社会网络数据。
(8) 需要不断地提升算法的扩展性。
(9) 选择合适的用户反馈方式。
(10) 设计合理的评测系统,时刻关注推荐系统各方面的性能。