平台:win10 x64 +VS 2015专业版 +opencv-2.4.11 + gtk_-bundle_2.24.10_win32
主要参考:1.代码:RobHess的SIFT源码
2.书:王永明 王贵锦 《图像局部不变性特征与描述》
SIFT四步骤和特征匹配及筛选:
步骤一:建立尺度空间,即建立高斯差分(DoG)金字塔dog_pyr
步骤二:在尺度空间中检测极值点,并进行精确定位和筛选创建默认大小的内存存储器
步骤三:特征点方向赋值,完成此步骤后,每个特征点有三个信息:位置、尺度、方向
步骤三:特征点方向赋值,完成此步骤后,每个特征点有三个信息:位置、尺度、方向
问题及解答:
(1)问题描述:怎么计算特征点的方向和幅值?思路是什么?
答:为了实现图像旋转的不变性,需要根据检测到的特征点的局部图像结构求得一个方向基准。我们使用图像梯度的方法求取该局部结构的稳定方向。对于己经检测到特征点,我们知道该特征点的尺度值σ,因此根据这一尺度值,在GSS中得到最接近这一尺度值的高斯图像。然后使用有限差分,计算以特征点为中心,以3X1.5σ为半径的区域内图像梯度的幅角和幅值,如下图所示。幅角和幅值计算公式加下:

参考书P130及图6-1
(2)问题描述:为什么要计算特征梯度直方图?怎么计算?
答:在完成特征点邻域的高斯图像的梯度计算后,使用直方图统计邻域内像素的梯度方向和幅值。梯度方向直方图的横轴是梯度方向角,纵轴是梯度方向角对应的(带高斯权重)梯度幅值累加值。梯度方向直方图将。0°~360°的范围,分为36个柱,每10°为一个柱。直方图的峰值代表了该特征点处邻域内图像梯度的主方向,也即该特征点的主方向,如下图所示:
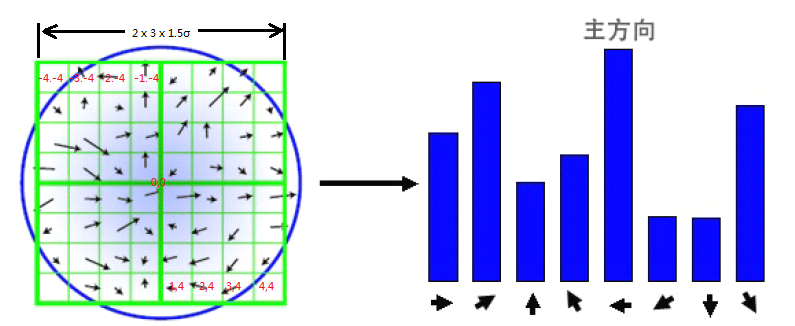
绿色格点代表邻域范围,蓝色圆圈代表格点的高斯权重(稍后介绍),黑色箭头指向代表梯度方向,箭头长度代表梯度幅值。右边为梯度方向直方图(36柱,每柱代表10°,上图只显示了8柱)。获得梯度方向直方图的步骤如下:
1)生成领域各像元的高斯权重。其中高斯函数方差为该特征点的特征尺度σ的1.5倍。形式如下,其中(i,j)为该点距离特征点的相对位置,如上图,左上角点像元距离特征点(0,0)(即中心点)的相对位置坐标为(-4,-4),同理,右下角像元为(4,4)。

2)遍历邻域(绿色)中每个点,判断其梯度方向,将其加入相应的梯度方向直方图中,加入量为其梯度幅值 * wi,j ,例如左上角(-4,-4)的点,其梯度为方向为25°,梯度幅值为mag,我们将其加入到hist[2]中(假设hist[0]为0°~10°的直方柱,hist[1]为10°~20°的直方柱,以此类推至hist[35]为350°~360°)。加入的量为mag* w(-4,-4),即hist[2] = hist[2] + mag* w(-4,-4)。直至遍历整个邻域,统计出该特征点出的梯度方向直方图。
3)平滑直方图。对上一步得出的直方图进行平滑,得到最终的梯度方向直方图。OpenCV中使用的 (1/16) * [1,4,6,4,1] 的高斯卷积和对直方图进行平滑处理,而vlfeat中使用了6次,邻域大小为3的平均处理,即hist[i] = (hist[i-1]+hist[i]+hist[i+1])/3。
参考书P131及图6-2
(3)问题描述:为什么每个点梯度幅值要使用高斯权重?
答:由于SIFT算法只考虑了尺度和旋转的不变性,并没有考虑仿射不变性。通过对各点梯度幅值进行高斯加权,使特征点附近的梯度幅值有较大的权重,这样可以部分弥补因没有仿射不变性而产生的特征点不稳定的问题。
(4)问题描述:如何确定特征点方向?
答:
有了梯度方向直方图之后,找到直方图中最大的值,则认为该方向为该特征点的主方向,如存在另一个方向大于最大值的80%,则认为该方向为该特征点的辅方向。一个特征点可能会有多个方向(一个主方向,一个以上的辅方向),这可以增强匹配的鲁棒性。具体而言,就是将该特征点复制成多份特征点(除了方向θ不同外,x,y,σ都相同)。
注意:在OpenCV中,若辅方向除了满足大于最大值80%外,还必须是局部最大值,即 hist[i] > hist[i-1] && hist[i] > hist[i+1]。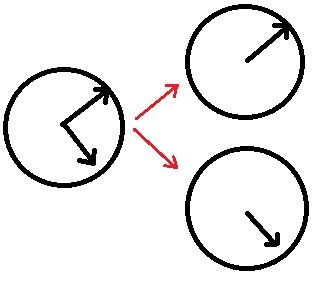
通常离散的梯度方向直方图,可以通过插值拟合处理,这样可以得到更精确的方向角度值。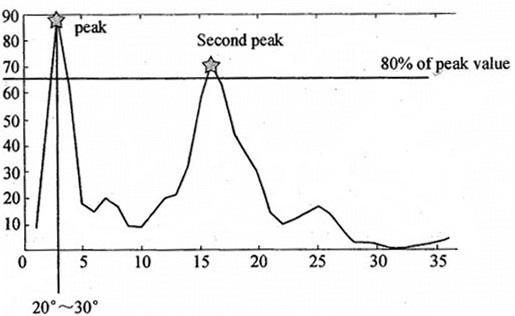
经过上述过程,我们特征点的所有量(x,y,σ,θ)都已经求得,其中位置(x,y)、尺度σ都是在上一节中求得,而特征点方向θ是通过特征点邻域直方图求得。下一节,将介绍SIFT描述子的形成方式。
参考书P132-P133及图6-5和图6-6
(5)问题描述:RobHess的SIFT源码如何实现步骤三,大概思路是这样的?
答:(5.1)代码及说明:
/*步骤三:特征点方向赋值,完成此步骤后,每个特征点有三个信息:位置、尺度、方向*/
//计算每个特征点的梯度直方图,找出其主方向,若一个特征点有不止一个主方向,将其分为两个特征点
calc_feature_oris( features, gauss_pyr );
(5.2)calc_feature_oris代码及说明:
确定关键点的大小和方向
/*计算每个特征点的梯度直方图,找出其主方向,若一个特征点有不止一个主方向,将其分
为两个特征点
参数:
features:特征点序列
gauss_pyr:高斯金字塔*/
static void calc_feature_oris( CvSeq* features, IplImage*** gauss_pyr )
{
struct feature* feat;
struct detection_data* ddata;
double* hist;//存放梯度直方图的数组
double omax;
int i, j, n = features->total;//特征点个数
//遍历特征点序列
for( i = 0; i < n; i++ )
{
//给每个特征点分配feature结构大小的内存
feat = malloc( sizeof( struct feature ) );
//移除列首元素,放到feat中
cvSeqPopFront( features, feat );
//调用宏feat_detection_data来提取参数feat中的feature_data成员并转换为
//detection_data类型的指针
//detection_data数据中存放有此特征点的行列坐标和尺度,以及所在的层和组
ddata = feat_detection_data( feat );
//计算指定像素点的梯度方向直方图,返回存放直方图的数组给hist
hist = ori_hist( gauss_pyr[ddata->octv][ddata->intvl], //特征点所在的图像
ddata->r, ddata->c, //特征点的行列坐标
SIFT_ORI_HIST_BINS, //默认的梯度直方图的bin(柱子)个数
cvRound( SIFT_ORI_RADIUS * ddata->scl_octv ),//特征点方向赋值过程中,搜索邻域
//的半径为:3 * 1.5 * σ
SIFT_ORI_SIG_FCTR * ddata->scl_octv ); //计算直翻图时梯度幅值的高斯权重
//的初始值
//对梯度直方图进行高斯平滑,弥补因没有仿射不变性而产生的特征点不稳定的问题,
//SIFT_ORI_SMOOTH_PASSES指定了平滑次数
for( j = 0; j < SIFT_ORI_SMOOTH_PASSES; j++ )
smooth_ori_hist( hist, SIFT_ORI_HIST_BINS );
//查找梯度直方图中主方向的梯度幅值,即查找直方图中最大bin的值,返回给omax
omax = dominant_ori( hist, SIFT_ORI_HIST_BINS );
/*若当前特征点的直方图中某个bin的值大于给定的阈值,则新生成一个特征点并添
加到特征点序列末尾传入的特征点指针feat是已经从特征点序列features中移除的,
所以即使此特征点没有辅方向(第二个大于幅值阈值的方向),在函数
add_good_ori_features中也会执行一次克隆feat,对其方向进行插值修正,并插入特征
点序列的操作幅值阈值一般设置为当前特征点的梯度直方图的最大bin值的80% */
add_good_ori_features( features, hist, SIFT_ORI_HIST_BINS,
omax * SIFT_ORI_PEAK_RATIO, feat );
//释放内存
free( ddata );
free( feat );
free( hist );
}
}
(5.2.1)cvSeqPopFront函数说明:
答:动态结构序列CvSeq是所有OpenCV动态数据结构的基础。
分为两类:
稠密序列
稀疏序列
(1) 稠密序列都派生自CvSeq,他们用来代表可扩展的一维数组 — 向量、栈、队列和双端队列。数据间不存在空隙(连续存储)。如果元素元素从序列中间被删除或插入新的元素到序列,那么此元素后边的相关元素全部被移动。
(2)稀疏序列派生自CvSet,CvSet也是基于CvSeq的,他们都是由节点所组成,每一个节点要么被占用,那么为空,由标志位flag决定。这些序列作为无序数据结构被使用,如点集合、图、Hash表等。
CvSeq的定义如下:
CV_TREE_NODE_FIELDS(CvSeq);
int total; //total表示稠密序列的元素个数,或者稀疏序列被分配的节点数。
int elem_size; //elem_size表示序列中每个元素占用的字节数。
schar* block_max; //block_max是最近一个内存的最大边界指针。
schar* ptr; //ptr表示当写指针。
int delta_elems; //delta_elems表示序列间隔尺寸。
CvMemStorage* storage; //storage指向序列存储的内存块的指针
CvSeqBlock* free_blocks; //free_blocks表示空的块列表。
CvSeqBlock* first; //first指向第一个序列块。h_next和h_prev并不是指向CvSeq内部元素的指针,它们是指向其它CvSeq的。
//头部添加
Char* cvSeqPushFront(CvSeq* seq,void* element=NULL);
//头部删除
Void cvSeqPopFront(CvSeq* seq,void* element=NULL);
参看:OpenCV——CvSeq动态结构序列——https://www.cnblogs.com/farewell-farewell/p/5999908.html
(5.2.2)ori_hist代码及说明:
答:
/*计算指定像素点的梯度方向直方图,返回存放直方图的数组
参数:
img:图像指针
r:特征点所在的行
c:特征点所在的列
n:直方图中柱(bin)的个数,默认是36
rad:区域半径,在此区域中计算梯度方向直方图
sigma:计算直翻图时梯度幅值的高斯权重的初始值
返回值:返回一个n元数组,其中是方向直方图的统计数据*/
static double* ori_hist( IplImage* img, int r, int c, int n, int rad, double sigma)
{
double* hist;//直方图数组
double mag, ori, w, exp_denom, PI2 = CV_PI * 2.0;
int bin, i, j;
//为直方图数组分配空间,共n个元素,n是柱的个数
hist = calloc( n, sizeof( double ) );
exp_denom = 2.0 * sigma * sigma;
//遍历以指定点为中心的搜索区域
for( i = -rad; i <= rad; i++ ) //范围为2*3*1.5σ,参看书P131图6-2
for( j = -rad; j <= rad; j++ )
//计算指定点的梯度的幅值mag和方向ori,返回值为1表示计算成功
if( calc_grad_mag_ori( img, r + i, c + j, &mag, &ori ) )
{
w = exp( -( i*i + j*j ) / exp_denom );//该点的梯度幅值权重
bin = cvRound( n * ( ori + CV_PI ) / PI2 );//计算梯度的方向对应的直方图中的bin下标
//ori范围(-Π,Π],+Π后范围(0,2Π]
bin = ( bin < n )? bin : 0; //把bin的下标归到0~36
hist[bin] += w * mag;//在直方图的某个bin中累加加权后的幅值
}
return hist;//返回直方图数组
}
(5.2.2.1)calc_grad_mag_ori代码及说明:
答:
/*计算指定点的梯度的幅值magnitude和方向orientation
参数:
img:图像指针
r:特征点所在的行
c:特征点所在的列
img:输出参数,此点的梯度幅值
ori:输出参数,此点的梯度方向
返回值:如果指定的点是合法点并已计算出幅值和方向,返回1;否则返回0*/
static int calc_grad_mag_ori( IplImage* img, int r, int c, double* mag, double* ori )
{
double dx, dy;
//对输入的坐标值进行检查
if( r > 0 && r < img->height - 1 && c > 0 && c < img->width - 1 )
{
//用差分近似代替偏导,来求梯度的幅值和方向
dx = pixval32f( img, r, c+1 ) - pixval32f( img, r, c-1 );//x方向偏导
dy = pixval32f( img, r-1, c ) - pixval32f( img, r+1, c );//y方向偏导
*mag = sqrt( dx*dx + dy*dy );//梯度的幅值,即梯度的模
*ori = atan2( dy, dx );//梯度的方向
return 1;
}
//行列坐标值不合法,返回0
else
return 0;
}
问题1:具体如何求梯度?为什么一阶偏导没有二分之一的系数?
答:差分代替偏导,一阶情况,具体参考:RobHess的SIFT代码解析步骤二(5.2.6.2.1.1)

参看博客:https://blog.csdn.net/lingyunxianhe/article/details/79063547 3.1.1、梯度的计算
问题2:为什么计算梯度的方向使用的是atan2,而不是(1)中介绍的arctan(atan)?
答:
说明:C 语言里 double atan2(double y,double x) 返回的是原点至点(x,y)的方位角,即与 x 轴的夹角。返回值的单位为弧度,取值范围为(-π, π]。结果为正表示从 X 轴逆时针旋转的角度,结果为负表示从 X 轴顺时针旋转的角度。
atan2与atan的区别:
atan接受的是一个正切值(直线的斜率)得到夹角,但是由于正切的规律性本可以有两个角度的但它却只返回一个,因为atan的值域是从-90~90 也就是它只处理一四象限,所以一般不用它。
atan2(double y,double x) 其中y代表已知点的Y坐标 同理x ,返回值是此点与远点连线与x轴正方向的夹角,这样它就可以处理四个象限的任意情况了,它的值域相应的也就是-180~180了。
例如:
例1:斜率是1的直线的夹角
cout<<atan(1.0)*180/PI;//45°
cout<<atan2(1.0,1.0)*180/PI;//45° 第一象限
cout<<atan2(-1.0,-1.0)*180/PI;//-135°第三象限
后两个斜率都是1 但是atan只能求出一个45°
例2:斜率是-1的直线的角度
cout<<atan(-1.0)*180/PI;//-45°
cout<<atan2(-1.0,1.0)*180/PI;//-45° y为负 在第四象限
cout<<atan2(1.0,-1.0)*180/PI;//135° x为负 在第二象限
后两个斜率都是-1 但是atan只能求出一个-45°
此处与书P130页不同,atan的值域[ -Π/2,Π/2],而atan2的值域[ -Π,Π],涵盖了一周360度(2Π)的范围。
参看博客:atan2相关知识汇总——https://blog.csdn.net/weixin_42142612/article/details/80972768
(5.2.2.2)梯度直方图某点梯度的幅值怎么计算?不是直接累加的,而是乘以一个高斯权重1.5sigma。
答:L为关键点所在的尺度空间值,按Lowe的建议,梯度的模值m(x,y)按 σ=1.5σ_oct 的高斯分布加成,按尺度采样的3σ原则,领域窗口半径为 3x1.5σ_oct。
在完成关键点的梯度计算后,使用直方图统计领域内像素的梯度和方向。梯度直方图将0~360度的方向范围分为36个柱(bins),其中每柱10度。如图5.1所示,直方图的峰值方向代表了关键点的主方向,(为简化,图中只画了八个方向的直方图)。
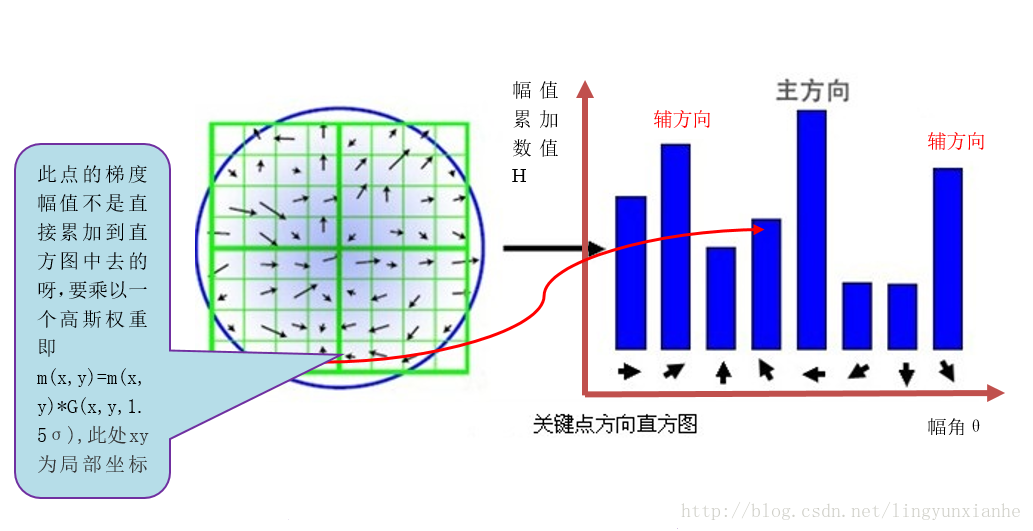
参看博客:https://blog.csdn.net/lingyunxianhe/article/details/79063547 3.1.1、梯度直方图
(5.2.3)smooth_ori_hist代码及说明:
答:
/*对梯度方向直方图进行高斯平滑,弥补因没有仿射不变性而产生的特征点不稳定的问题
参数:
hist:存放梯度直方图的数组
n:梯度直方图中bin的个数*/
static void smooth_ori_hist( double* hist, int n )
{
double prev, tmp, h0 = hist[0];
int i;
prev = hist[n-1];
//类似均值漂移的一种邻域平滑,减少突变的影响
for( i = 0; i < n; i++ )
{
tmp = hist[i];
hist[i] = 0.25 * prev + 0.5 * hist[i] +
0.25 * ( ( i+1 == n )? h0 : hist[i+1] );
prev = tmp;
}
}
问题1:为什么要进行高斯平滑?
答:为了防止某个梯度方向角度因受到噪声的干扰而突变,我们还需要对梯度方向直方图进行平滑处理。Opencv 所使用的平滑公式为:
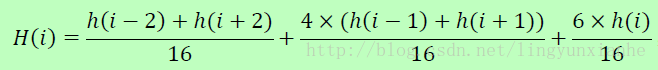
1)今天的内容是是平滑,先介绍均值和高斯平滑,高斯平滑是均值平滑的一个扩展,或者是一个进化版本。均值的原理是,一个规定的邻域内,所有像素的平局值作为最终计算的结果,每个像素的权值相同,为总像素的倒数,而高斯平滑是上述的升级版本,邻域内每个像素的权值不同,而权值是由高斯函数确定的。
均值平滑和高斯平滑都是线性的,也就是,一旦参数给定,模板就确定下来,不会因为位置和像素分布不同而改变,而线性模板的基本运算是卷积。
线性模板的另一个性质就是可以进行频域分析,比如高斯平滑的频域仍然是高斯的,而且是低通的,这与前面讲到的平滑是消除尖锐的噪声(高频)的操作相互证明了其正确性,均值平滑是一个盒状滤波器,其频域为sinc函数,也是一个近似的低通,但sinc函数有旁瓣,所以,模板宽度选择不好可能会有一些不好的效果,比如有些高频会被保留,这一点也比较好理解。
比较下两种均值(加权和不加权)。比如一维的一个序列{0,0,0,0,0,1000,0,0,0,0},明显1000是个边缘,如果使用3个宽度的均值平滑,结果是{0,0,0,0,333,333,333,0,0,0},边缘被完全模糊掉了。但如果使用{1,2,1}的近似高斯平滑模板,结果是{0,0,0,0,250,500,250,0,0,0},边缘被保留。所以,加权平均(高斯)可以保留一定的细节。
参看博客:灰度图像--图像增强 平滑之均值滤波、高斯滤波——http://www.mamicode.com/info-detail-447178.html
2)LOWE建议对直方图进行平滑,降低突变的影响,弥补因没有仿射不变性而产生的特征点不稳定的问题
问题2:对梯度直方图进行高斯平滑,为什么用的是1/4{1,2,1}?盒子滤波器的模板吗?
答:用的是1/4{1,2,1}不是盒子滤波器的模板,1/4{1,2,1}是高斯加权平均。参看:https://www.cnblogs.com/liguangsunls/p/6785878.html 6.2 平滑直方图 lowe建议对直方图进行平滑,降低突变的影响。
(5.2.4)dominant_ori代码及说明:
答:
/*查找梯度直方图中主方向的梯度幅值,即查找直方图中最大bin的值
参数:
hist:存放直方图的数组
n:直方图中bin的个数
返回值:返回直方图中最大的bin的值*/
static double dominant_ori( double* hist, int n )
{
double omax;
int maxbin, i;
omax = hist[0];
maxbin = 0;
//遍历直方图,找到最大的bin
for( i = 1; i < n; i++ )
if( hist[i] > omax )
{
omax = hist[i];
maxbin = i;
}
return omax;//返回最大的bin的值
}
(5.2.5)add_good_ori_features代码及说明:
答:
/*若当前特征点的直方图中某个bin的值大于给定的阈值,则新生成一个特征点并添加到特征点序列末尾
传入的特征点指针feat是已经从特征点序列features中移除的,所以即使此特征点没有辅方向(第二个大于幅值阈值的方向)
也会执行一次克隆feat,对其方向进行插值修正,并插入特征点序列的操作
参数:
features:特征点序列
hist:梯度直方图
n:直方图中bin的个数
mag_thr:幅值阈值,若直方图中有bin的值大于此阈值,则增加新特征点
feat:一个特征点指针,新的特征点克隆自feat,但方向不同
*/
static void add_good_ori_features( CvSeq* features, double* hist, int n,
double mag_thr, struct feature* feat )
{
struct feature* new_feat;
double bin, PI2 = CV_PI * 2.0;
int l, r, i;
//遍历直方图
for( i = 0; i < n; i++ )
{
l = ( i == 0 )? n - 1 : i-1;//前一个(左边的)bin的下标
r = ( i + 1 ) % n;//后一个(右边的)bin的下标
//若当前的bin是局部极值(比前一个和后一个bin都大),并且值大于给定的幅值阈值,则新生成一个特征点并添加到特征点序列末尾
if( hist[i] > hist[l] && hist[i] > hist[r] && hist[i] >= mag_thr )
{
//根据左、中、右三个bin的值对当前bin进行直方图插值
bin = i + interp_hist_peak( hist[l], hist[i], hist[r] );
bin = ( bin < 0 )? n + bin : ( bin >= n )? bin - n : bin;//将插值结果规范到[0,n]内
new_feat = clone_feature( feat );//克隆当前特征点为新特征点
new_feat->ori = ( ( PI2 * bin ) / n ) - CV_PI;//新特征点的方向
//方向还原为(Π,Π],bin最大值36,2Π*36/36-Π=Π,bin最大值0,2Π*0/36-Π=-Π
cvSeqPush( features, new_feat );//插入到特征点序列末尾
free( new_feat );
}
}
}
问题1:插值时小柱子到边界怎么处理,怎么插值?因为抛物线插值需要利用三个点的坐标,如0之前和35之后怎么处理?
答:由于角度是循环的,即00=3600,如果出现h(j),j超出了(0,…,35)的范围,那么可以通过圆周循环的方法找到它所对应的、在00=3600之间的值,如h(-1) = h(35)。把小柱子看成是循环的,角度的取值为0~360度是一个圆周,0之前利用标号为35的小柱子和35之后利用标号为0的小柱子。
参看博客:https://blog.csdn.net/lingyunxianhe/article/details/79063547 3.2.1、梯度图像的平滑处理
问题2:对直方图采用什么插值?插值需要利用几个点的坐标?
答:采用抛物线插值,需要三个点的坐标,hist[l], hist[i], hist[r],传入interp_hist_peak函数。
(5.2.5.1)interp_hist_peak代码及说明:
答:
//根据左、中、右三个bin的值对当前bin进行直方图插值,以求取更精确的方向角度值
#define interp_hist_peak( l, c, r ) ( 0.5 * ((l)-(r)) / ((l) - 2.0*(c) + (r)) )
问题:梯度直方图抛物线插值 小柱子在直方图中的索引号的公式怎么计算?

假设我们在第i个小柱子要找一个精确的方向,那么由上面分析知道:
设插值抛物线方程为h(t)=at2+bt+c,其中a、b、c为抛物线的系数,t为自变量,t∈[-1,1],此抛物线求导并令它等于0。
即h(t)´=0 得tmax=-b/(2a)
现在把这三个插值点带入方程可得:

参看博客:https://blog.csdn.net/lingyunxianhe/article/details/79063547 3.2.2、梯度直方图抛物线插值
(5.2.5.2) clone_feature代码及说明:
答:
/*对输入的feature结构特征点做深拷贝,返回克隆生成的特征点的指针
参数:
feat:将要被克隆的特征点的指针
返回值:拷贝生成的特征点的指针
*/
static struct feature* clone_feature( struct feature* feat )
{
struct feature* new_feat;
struct detection_data* ddata;
//为一个feature结构分配空间并初始化
new_feat = new_feature(); //参看RobHess的SIFT代码解析步骤二(5.2.6.4)new_feature()代码及说明
//调用宏feat_detection_data来提取参数feat中的feature_data成员并转换为detection_data类型的指针
ddata = feat_detection_data( new_feat );
//对内存空间进行赋值
memcpy( new_feat, feat, sizeof( struct feature ) );
memcpy( ddata, feat_detection_data(feat), sizeof( struct detection_data ) );
new_feat->feature_data = ddata;
return new_feat;//返回克隆生成的特征点的指针
}
问题:memcpy的函数功能?strcpy和memcpy的区别?
答:所需头文件:C语言:#include<string.h>;C++:#include<cstring>
函数原型:
void *memcpy(void *dest, const void *src, size_t n);
功能:
从源src所指的内存地址的起始位置开始拷贝n个字节到目标dest所指的内存地址的起始位置中
参看:百度百科——https://baike.baidu.com/item/memcpy/659918