Computer Vision_2_Active Shape Models：Active Shape Models-Their Training and Application——1995

此为计算机视觉部分，主要侧重在底层特征提取，视频分析，跟踪，目标检测和识别方面等方面。

1. Active Appearance Models
活动表观模型和活动轮廓模型基本思想来源 Snake，现在在人脸三维建模方 面得到了很成功的应用，这里列出了三篇最早最经典的文章。对这个领域有兴趣 的可以从这三篇文章开始入手。
[1998 ECCV] Active Appearance Models
[2001 PAMI] Active Appearance Models

2. Active Shape Models
[1995 CVIU] Active Shape Models-Their Training and Application

翻译

主动形状模型，他们的训练和应用

摘要 -基于模型的视觉被牢固地建立为健壮的方法来识别和噪声，杂波和遮挡的存在定位已知的刚性物体。更成问题的基于模型的方法应用于对象其外观可以改变的图像，虽然已经提出了许多基于使用的灵活的模板方法。与现有方法的问题是，他们牺牲模型的特异性，以适应变化，从而影像解译中牺牲了鲁棒性。我们认为，一个模型应该只能够在它代表对象的方法的类的特征变形。我们描述了通过从训练正确设置了注释的图像的学习变异的模式建立模型的方法。这些模型可用于在迭代细化算法类似于由主动轮廓模型（Snakes）中使用的图像搜索。关键的区别是，我们主动形状模型只能变形以适应方式与训练集一致的数据。我们发现，我们已经建立这样的模型，并用它们定位在嘈杂，混乱的图像部分被遮挡物体的几个实际的例子。

1 引言

我们应对图​​像定位已知对象的实例的问题。利用刚性模型图像判读是公认的[1,2]。然而，在同级别的许多实际情况中的对象是不相同的和僵化模式是不合适的。在医疗应用中，例如，器官的形状可以通过相当时间和因人而异。此外，许多工业应用涉及具有运动部件，或组件其外观可以变化的组件。在这种情况下灵活的模型，或可变形的模板，可以用来允许在成像的对象[3-23]的形状一定程度的可变性。
 在本文中，我们提出了构建和使用图像结构，其形状可以变化的灵活模式的新方法。该模型能够一类形状的内捕捉自然变异，可以在图像搜索来寻找结构的他们代表的例子。以前的方法已经允许模型变形，但没有量身定做的变化对类形状的关注，该模型是不特定的。我们的主要贡献是描述如何创建模型，其允许相当大的变化，但仍然专门用于该类他们所代表的结构。
 我们的技术依赖于每个对象或图像结构通过一组点来表示。这些点可以表示的边界，内部特征，或甚至外部的，如边界的凹部的中心。点被放置在每个训练集的对象的示例的相同的方式。这是手工完成，虽然工具可以帮助用户。点的集合被自动对齐，以尽量减少在等效点之间的距离的方差。通过检查标记点的“点分布模型”推导的位置的统计数据，模型给出了点的平均仓位，并拥有一批其控制在训练集找到变异的主要模式参数。

鉴于这样的模型和含有建模，图像判读涉及选择用于每个参数的值，以找到模型到图像的最佳拟合的对象的一个​​例子的图像。我们描述了一种技术，它允许为最佳形状，取向，尺寸和位置的初始非常粗略估计到由假设的模型实例与图像数据进行比较，并使用模型和图像之间的差异而变形的形状加以改进。之前我们已经介绍了如何获得初始猜测[7]。该方法具有与Kass等人的活动轮廓模型（或Snakes）的相似性[3]，但不同之处被施加，全球形状约束；进行这种区分清楚我们采用的术语主动形状模型。关键的一点是，该模型的情况下，可以在训练集中找到了唯一的变形。
 我们的结果表明，用于构建模型与活性匹配技术相结合的方法提供了复杂的图像的解释系统有效的范例。在我们回顾一些相关文献的本文的其余部分，描述了建模方法，并显示的训练的模型例子。有源匹配技术被描述和结果列，示出了模型可以如何被用于解释图像。
 

2 背景
没有描述使用灵活的模型或变形模板，以帮助图像解译大幅文献。这样的模型通常具有许多参数来控制的形状和模型的全部或部分的姿势。我们给一些最之意义的工作，这主要涉及到二维图像的简要回顾。

2.1 “手工制作”模式
灵活的模型可以从简单的子组件，如圆，直线或圆弧，这是允许一定程度的自由度相对走动彼此，并可能改变规模和方向来建立。 Yuille等人[5]脸部模型部分，如眼睛和嘴巴，用这种方式。当试图以适应模型的图像，他们首先获得近似配合，它们通过一次改变模型，一个的不同部分缩小。Lipson等人[6]应用类似的方案椎骨的椭圆模型映射到脊椎的CT图像。 Hill等人[7]使用心脏的手工模型，结合遗传算法搜索查找超声心动图左心室。

虽然这种模式可以捕捉预计形状的详细知识，该方法缺乏通用性。有必要来设计一个新的模型和配件为每个应用程序图像的方案。

2.2 铰接式模型
许多作者认为通过滑动或旋转接头连接的刚性部件内置关节模型。 Beinglass和Wolfson[8]描述用于定位使用通用霍夫变换与关节运动的点作为基准点用于每个子部分这样的对象的方案。连接子部分则投给了相同的参考点。 Grimson [2]已经扩大了他的“解释树”的方法来识别物体，包括一些关节，并审查了其他工作沿着相同的路线。这种方法只适用于受限制的类的可变形状的问题。

 2.3 主动轮廓模型（“Snakes“）
Kass等人[3]描述了被吸引到的图像特征灵活的轮廓模型。这些能量最小化样条曲线被建模为具有的刚度和弹性，并且朝向的功能，如线和边吸引。约束可以应用，以确保它们保持光滑和限制的程度，他们可以弯曲。

Snakes蛇可以被视为参数化模型，参数是样条控制点。它们通常是自由采取几乎任何光滑边界与他们的整体形状约束很少。通过使用图像证据力施加到模型和最小化能量函数的拟合想法是有效的。
 Hinton等人[4]描述一种类型由许多控制点已经优选的“家”位置，得到snake蛇特定默认形状支配花键snake蛇的。变形是通过移动控制点从他们的“家”的位置离开造成的。虽然对象的平均形状被表示，形状变化的模式仅由粗略的数量和控制点的位置来定义。

 2.4 傅立叶级数形状模型
Scott[9]通过三角函数的膨胀提出造型形状的方法，

 

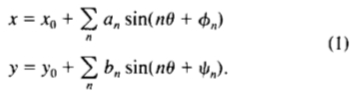
产生的形状为参数的函数。通过改变参数和使用的术语的数目，可以产生不同的形状。斯科特显示了如何通过改变参数，以适应这样的形状模型的图像数据，以最小化能量术语。该模型是几乎可以无限变形，并且不包含之前形状的信息。 Staib和Duncan[10]描述了类似的傅立叶模型，并用它们来解释医学图像。他们得出的分布对于每个参数在训练集的同时拟合模型到图​​像最大化概率测度确定的可能性有多大，目前的示例是所期望的对象。
Staib和Duncan[11]描述了这样的技术如何可以用于在医学图像中的器官建模。一个给定的形状通过对参数的值的列表来表示，并且通过改变从这些值的参数变形。他们描述了通过应用约束模型的参数包含几个灵活的对象之间的关系的方式。
 三角函数基函数是不适合用于描述一般的形状；例如，使用术语的有限数，它们只能近似方形角落。在三角展开的参数中形状的变化和变型之间的关系并不简单。

2.5 形状的统计模型
许多工人已经研究组的这标志着对象上显著位置“地标”点分布。Goodall[14]讨论了登记的任意维数的形状和用于估计平均形状使用普鲁克分析和界标点坐标之间并用于评估集形状之间的差的协方差。
 Grenander等人[12]描述表示形状为一组由弧连接边界点的方法，与相邻弧之间的关系的统计模型。他们展示如何手的轮廓模型可以被操纵，以适应手的退化图像。他们这样做是考虑边界的部分，并确定给定的边界和局部图像数据的其余部分其最可能的位置。通过在多个扫描的过程进行迭代，以溶液的穿过边界。Grenander和Miller [13]已经扩展这项工作包括灰度信息和多个模型。Mardia等人[15]做同样的事情，表示为点与由协方差矩阵的相关分布的序列的形状的边界。他们也通过记分周期内找到给出的图像和当前的形状最可能的位置。Grenander等人和Mardia等人都代表形状，在复平面上的点集。这些点可以关于以下与协方差矩阵S，其中S是使用任一阶自回归条件（CAR）模型或Toeplitz托普利兹协方差矩阵建模为正态分布他们的手段而变化。在我们的工作中，我们使用了类似的底层模型，但要避免点的序列的任何依赖性，从而获取更多的全球形状属性。我们还使用主成分分析，以简化的协方差矩阵的结构。

2.6 有限元模型
有限元方法可用于以可变的图像对象与内部的刚度和弹性的物理实体建模。Pentland[18]和 Pentland和Sclaroff [19]使用那个像弹性粘土的团块三维模型。他们得出合适的碱的形状的振动的模式，例如椭圆体，并建立从不同的振动模式的形状。第一模式是形状的大型的变化；高阶模是更本地化。为了模拟人的头，他们使用的第一个30种模式。他们能够适应模型由一个交互过程范围的数据，可以通过比较参数比较不同的头。 Terzopoulos和Metaxas [20]提出使用可变形的超二次曲面类似的想法。 Nastar和Ayache [21]使用该形状的一个例子的振动模式使用有限元方法来进行建模。 Karaolani等人[22,23]使用有限元方法来二维对象的模型，给予的替代Kass的“Snakes”等人[3]。
所有这些方法具有的优点是模型是比较容易构建，并且允许一个家庭形状的紧凑参数表示。

2.7 为更好的模式的需求
我们已经描述了许多的现有方法用于创建和使用可变形模型来解释包含可变形式的结构的图像。它在这一点上，为什么我们认为需要一种新的方法来解释是很重要的。我们认为，问题的关键是模型的特殊性之一。必要的是，可变形的模式应该是能够容纳在它被用来代表的对象发现的变化范围，但还不够。模型的主要作用是促进强大的自动解释即使在嘈杂或杂乱或者感兴趣的对象的部分可能被遮挡图像。如果模型是非特异性的，在某种意义上说，它是能变形，以表示它们是不是类的有效实例对象的认可，那么这种稳健性受到损害。我们的目标是开发模式，只能在它们所代表的对象的特有的方式变形。在一般情况下，其可变性引起的机制不足够很好的理解，以允许提出变形的理论模型。唯一现实的办法是从有代表性的训练集结构的“学习”变化的特定模式来进行建模。其他人试图通过将模型参数限制从训练集确定其分布的基础上，类似的东西。如果象通常的情况中，模型参数在训练集合相关，这种方法不能有效地限制可产生于那些类似于在原始训练组（见图1）中发现的形状。我们的做法是找到形状表示，其中形状参数是在训练集不相关的基础。在这种情况下对每个参数的简单限制约束模型来生成类似的在训练集中的形状。我们还表明，它是直接在图像解译使用这些模型。

图1：如果两个或更多形状的参数（s1和s2）是在一组形状的相关然后简单的范围的参数不限制的形状，以那些类似于原始集合。

3.点分布模型

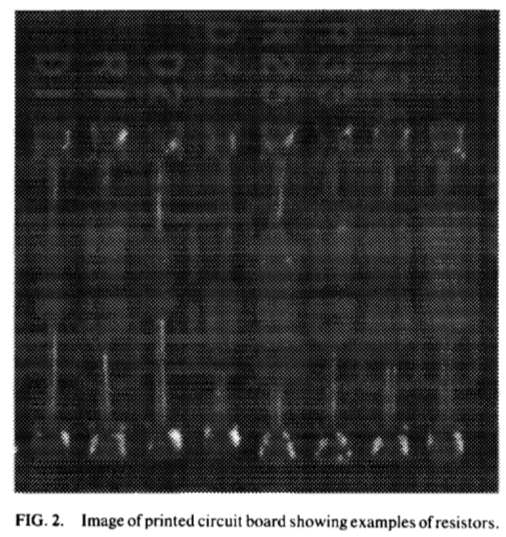
图2：印刷电路板的图像显示了电阻器的例子

图3：从训练集中电阻形状的例子。

假设我们希望得到一个模型，因为它们出现在印刷电路板上来表示电阻器的形状，如图2电阻器的不同示例具有足够不同的形状，使得一个刚性模型是不恰当的。图3示出了从各个电阻的背光图像获得的电阻器的边界的一些例子。我们的目标是建立描述两种典型的形状和典型变化的模型，

使用图3的实施例中作为训练集。我们通过表示各实施例中作为一组标记的“里程碑”的点，计算该点的平均值的位置，并且其中从每个实施例中的点倾向于从平均值变化的主要方式实现这一点。
 

3.1 标注的训练集

图4：边界的三十二个点模型

为了形状模型中，我们通过一组点的代表。对于电阻器，我们选择放置的边界周围的点，如示于图4。这必须在训练集中的每一个的形状来完成。该点的标签是非常重要的。每个标记点表示该对象或其边界的特定部分。例如，在电阻器模型，点0和31总是代表一个金属丝的端部，分3，4，和5代表了电阻器的主体的一端，并依此类推。该方法通过模拟标记点有什么不同倾向的形状各异一起移动。如果标记是不正确，与放置在每个训练形状不同的网站上的特定点，则该方法将无法可靠地捕获形状可变性。在点以下所示的实施例中任一手动放置在每个图像上，或工具被用来标记在手工分割边界点。值得注意的是，点仅在训练阶段期间手动放置；没有必要提前找到这些点，当模型用于图像解释，我们后来如何被隐含使用自动方法实现形容。

Bookstein [16，17]在生物学和医学标本的图像，以便检查和测量可以与其它因素相关联形状的改变标记的显著点。我们使用代表点来捕捉形状制约因素，并可以用于构造形状的图像解释使用似是而非的新实例模型。 Bookstein称他的代表点“标志点”，并介绍了他们在实用性方面。对于我们而言，他们可以减少到三种不同类型：
　　1.点标记与特定应用程序相关的显着性，诸如眼睛的面部或边界的尖角的模型的中心的对象的部分；
　　2.点标记与应用程序无关的事，诸如在一个特定的取向的物体，或曲率极值上的最高点；

　　3.可以从类型1和2的点被内插的其它点；例如，蓬标记以相同的间距圆2层1类型的地标之间的边界。

 在图4所示的点0，3，5，10等标记容易识别的特征，因此是类型1。其它点等间距分布之间的边界间隔开，等等都是类型3地标点类型的点的电阻器I型是优选的那些类型2的，因为它们是在一般更容易识别准确。然而，2型和3型的点几乎总是必要定义足够详细的柔性形状的边界是有用的。
 需要注意的是标志性的点是非常重要的，可以用来描述单个对象或一组空间相关的对象，该点可能来自结构的几个不同的组件。通常我们使用的边界点，和准边界节段用适当的对标志点。虽然我们已经实现并研究利用样条插值生成使用最少的一组，我们发现，简单地用足够的类型3点来描述曲线足够的精度是有效的，在计算上更高效地标边界。

3.2 对齐训练集
我们的建模方法通过检查了训练集的标记点的坐标的统计数据。为了能够等效点从不同的形状比较，它们必须相对于一组轴的对准。我们通过缩放，旋转和平移训练的形状，使他们尽可能紧密对应地实现所需的对准。我们的目标是尽量减少对不同形状的等效点之间的距离的平方的加权和。这是Procrustes(普鲁克)方法[24]的变形例。
 我们首先考虑对准一对形状。令x是描述在该组的第i个形状的n个点的矢量：

 

设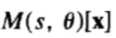是通过旋转和由缩放s。给定两个相似的形状，，我们可以选择和平移映射到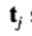，以便最小化的加权和

 

其中：

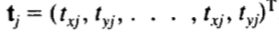
和 W是权重为每个点的对角矩阵。
详细情况见附录A.
权重可以选择给更多的意义那些往往是最“稳定”在其中走动至少相对于在形状其他点设置的那些点。我们已经使用所限定的权重矩阵，如下所示：让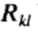是点k 和l 的形状之间的距离；让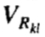的，在该距离超过设定的形状的方差；我们可以选择一个权重，对于第k个点使用

 

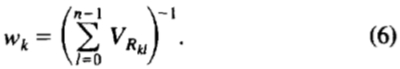
如果一个点往往很大走动相对于在形状等穴，方差之和将是大的，和低体重会给出。然而，如果一个点趋向于保持固定相对于其他人，方差之和将是小的，大的权重将给出并在不同的形状匹配的这样的点会是当务之急。
 我们用下面的算法来对齐一组N个形状；
　　·旋转，缩放，和每个形状与该组中的第一形状对齐平移。
　　·重复
　　　　·从对齐的形状计算平均形状。
　　　　·归一化的当前平均值的取向，比例和原点到合适的默认值。
　　　　·重新调整各种形状与当前的平均值。
　　·直到过程收敛。

标准化平均到默认比例和每次迭代中提出的要求，以保证算法收敛。如果没有这种实际上有 4（N-1）上 4N 变量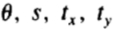（为每个所述N个形状的）和约束所述算法是病态-平均会收缩，旋转，或滑落到无穷。在平均的姿态和规模的限制使方程有一个独特的解决方案。任一平均值被缩放，旋转和平移，使得它的第一形状相匹配，或任意的默认设置可被使用，诸如在它的重心，取向，使得所述形状的特定部分是在所述选择的原点顶部和体重秤，使得两个选定点之间的距离为一个单位。注意，归一化所述当前平均形状，然后对准形状以匹配是不一样的归一化每个单独的形状。如果每个形状是通过设置一特定两点之间的距离为一个单位的规模标准化，人工相关性可能会因该组被强制，扭曲模型。但是，如果每个形状与均值一致，每次都会有类似规模，平均的。在这种情况下，具有里程碑意义的点位置将选择以最佳匹配均值，而不是硬性规定。这导致更好的模型。
 所述对准过程中的收敛条件可以通过检查每个形状对准到重新计算的平均值和恒等变换所需要的变换之间的平均差异被测试。
 实验表明，该方法收敛到相同的结果，其独立的形状在第一平台上排列，尽管收敛的正式证明还没有被设计出来。我们考虑的解决方案直接的方法，但发现与数值稳定性问题。 由于计算效率模型构建过程中是不是一个问题的迭代方法是足够我们的目的。

3.3 捕捉组对齐形状的统计

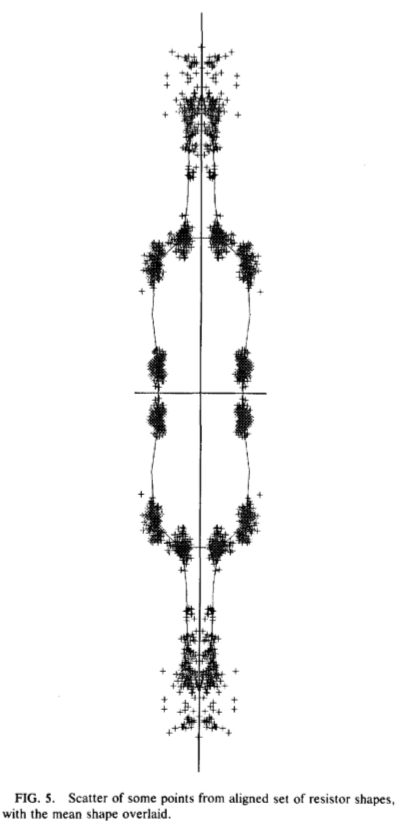
FlG.5：从对齐设置电阻器形状的一些点的散射，具有覆盖在平均形状。

在图5的一些对准的电阻形状的顶点的坐标被绘制，以覆盖在平均形状。由此可以看出，某些顶点显示在训练集很小的变化，而其他形成更多的弥漫“云”中的点分布模型（PDM）寻求这些云内的坐标的变化建模。但是，它必须是记住，地标不会对独立运动 - 它们的位置部分相关。
 在训练集合中的每个实例中，当比对时，可以通过在2n维空间中的单个点表示（见公式（2））。因此一组N个例子形状给出的N个点在该2n个维空间中的云。我们假设这些点位于的空间，我们称之为“允许形状域”的一些区域内，并且该分给这个区域的形状和大小的指示。这一领域中的每一个2n-D点给出一组地标，其形状大致类似于那些在原有训练集。因此，通过移动有关允许的形状域名，我们可以生成以系统的方式新的形状。下面给出的方法试图这个云的形状模型在高维空间，因此捕捉到个别地标点的位置之间的关系。我们作一个假设，云约为椭圆形，并继续计算其中心（给予平均形状）和它的主轴，这给周围的云移动的方式。稍后我们将讨论这个椭圆形的假设打破的影响。
 给定一组N个排列的形状，平均形状，（椭圆形状允许域的中心），利用计算出

 

一个2n-D的主轴椭圆体拟合到数据可以通过应用主成分分析（PCA）到数据[25]进行计算。每个轴提供了一个“变化模式”，其中，所述标志点倾向于作为形状变化一起移动的一种方式。对于在训练集中的每个形状，我们计算从平均值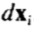，，其中的偏差

 

然后，我们可以计算出2n×2n 协方差矩阵，S，使用

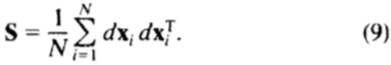
椭圆体的主轴，赋予该形状的点的变化的模式，是由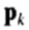描述后，S的单位向量，使得

（其中，是S的第k个特征值，），

 

可以示出的是对应于最大特征值的协方差矩阵的特征向量描述椭圆体的最长轴线，并且因此在用于导出协方差矩阵中的变量变化的最显著模式。由每个特征向量解释的方差等于相应的特征值[25]。 大部分的变化通常可以通过一个小的数量的模式进行说明，t. 这意味着，对从2n维椭球体是通过在三维椭圆体，其中 t 是选定的，使得原始椭圆体具有沿轴线 t + 1 和相对小的宽度近似以上。用于计算t的一个方法是选择最小数量的模式，使得它们的方差的和解释的足够大的比例入的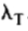，所有的变量的总方差，其中

 

在我们的容许形状域（即，任何允许的形状）的任何点可以通过取均值并添加本征向量的线性组合来达到。第k个特征向量由沿着平行于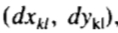，它是从第 l 对在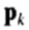元得到的矢量移动它影响在模型点升：

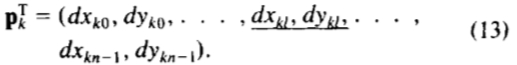
 在训练组中的形状可以利用平均形状并且从第1 t 模式获得的这些偏差的加权和来近似：

 

上述方程允许我们通过改变花色能够限制内的参数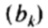中，以产生形状的新的例子，因此，新的形状将是类似于那些在训练集中。参数是线性独立的，虽然有可能是非线性的依赖性仍然存在。 用于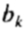的限值通过检查来生成训练集所需要的参数值的分布的。由于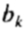在训练集的方差可以示出为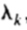，在合适的限度通常是顺序的

 

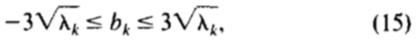
因为大多数人口处于在均值的三倍标准差。
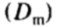 可替换地，可以选择参数集，使得来自平均值的马氏距离小于一个合适的值，：

 

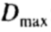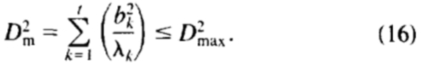
如果每个形状参数是正态分布然后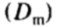将是卡方分布，和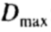可以被选择为包括可能的实现的适当大的比例。
 

3.4 实践例
上述技术已被用于产生用于两个人造和生物对象点的分布模型（PDMs）。我们提出结果在图3中，一组心脏心室的形状示出的设置电阻器的形状，以及一组手形状。其它实例已在别处[33,34]中所述。

3.4.1 电阻器的型号
在图3中示出的电阻器的形状采用上述，与缩放，从而从它们的重心的点的平均距离的平均形状的方法是对准一个单元。
 图5显示了平均形状。导出的协方差矩阵的最显著特征值示于表1中。

表1：从一组电阻器形状的派生的协方差矩阵的特征值

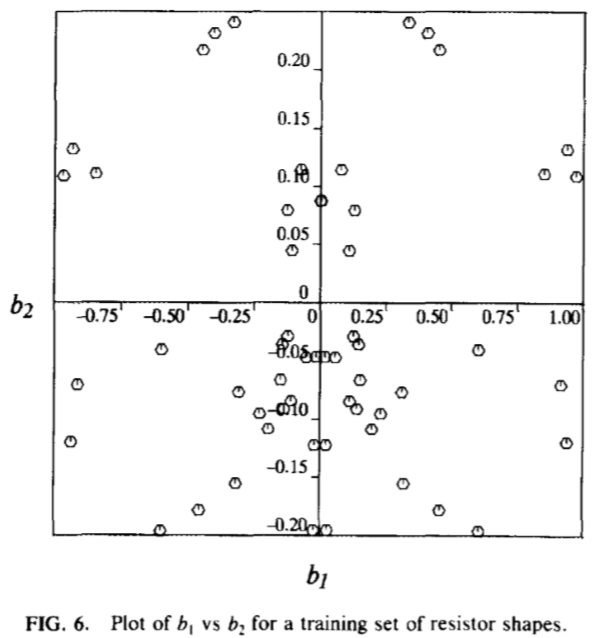
图6：b1的情节VS b2的训练集电阻器的形状

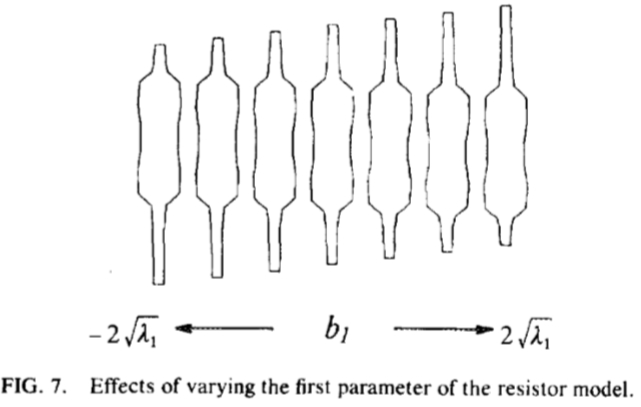
图7：改变电阻器模型的第一参数的影响。

图8：改变电阻器模型的第二个参数的影响。

图9：改变电阻器模型的第三个参数的影响。

 图6显示了b1 VS b2，对于训练集的情节。缺乏散点图结构的建议，参数可以作为独立的处理。目前，我们正在努力获得独立的比较正式的测试。这些参数之间的依赖就意味着原来的点位置之间的非线性关系，将导致参数生成“非法”的形状一些组合。通过改变前三个参数分别我们可以生成如图7-9的形状的例子。每个参数的表示可以频繁地随变形的直观描述相关联的形状的变化的模式。比较图7-9与图3改变第一参数（b1）调整所述电阻器向上的本体和沿着电线的位置。第二个参数变化的电阻器，锥形和正方形之间的主体的端部的形状。第三个参数会影响线中的任一端的曲率。随后的参数有较小的影响，包括导线以相反的方向弯曲。变化的这些模式有效地捕捉存在于训练集的可变性。注意，在图3中的各个点的位置显然大的变化实际上是在高度受限，并且在形状上总体变化可以通过一个小的数量的模式进行说明。该模型已被用于定位图像电阻（见下文）。

图10：每片含96点心脏心室的形状的例子。

表2：从一组心室形状的派生的协方差矩阵的特征值

图11：b1 VS b2对于训练集的心脏心室的例子。

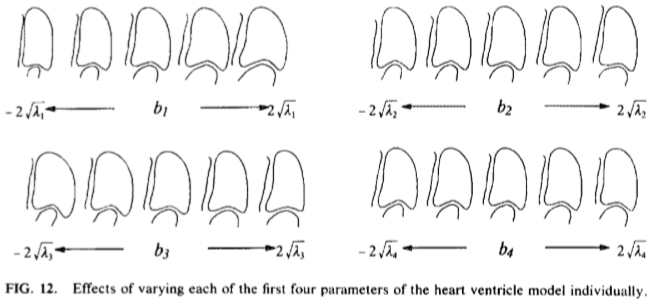
图12：单独改变每个心脏心室模型的前四个参数的影响。

 3.4.2 心脏模型
图10示出从一组通过询问心脏病专家来绘制在超声心动图图像而获得66层心脏腔室的边界的例子。每个结构是由96分表示。这个例子显示了一个模型如何代表几个形状以及它们之间的空间关系。形状变化产生于两个来源：训练集是从数个个体衍生的，并且在每种情况下，从不同的阶段中的心动周期，在此期间的心脏腔室的尺寸和形状可显着改变拍摄的图像。该点代表左心室的左心房的边界（心室下面在附图中）的边界处，右心室的边界的一部分，和部分。表2示出了用于训练集获得的协方差矩阵的特征值。
 图11表明b1和b2，再次是独立的，并且图重构通过依次改变前四个模型参数而获得的形状图12示出。第一参数变化的形状的宽度。第二个参数变化的隔膜的外观（壁从右心室分离左）。第三和第四个参数而变化左心室的形状和下面的心房的建模部件。应当强调的是，这些模式被完全自动地导出，并且从数据的变化的统计分析产生。
 该模型已被用于定位在超声心动图一个心脏左心室的边界（参见下文，也[26]）。

图13：培训手形的集合，每一个由72个点定义。

图14：单独改变每个手模型的前三个参数的影响。

3.4.3 手板模型
一组18的手形，从（图13）的作者之一的右手的图像生成。每个由边界周围72分表示。这些由在端部和手指的关节12个定位地标点和在静止沿着连接边界同样填充种植在例子。一个模型被训练上的数据，并且发现，该方差的96％可以通过变化的一次6种模式进行说明。第一三种模式显示在图14中，并且由所述的手指的运动的组合。再次，一个紧凑的参数化的模型已经产生，其已经用于定位图像中的手（见下文）。

3.4.4 在PDM的蠕虫模型的局限性
我们已经发现，上述的线性模型是有效的一个非常广泛的应用。但是，有一些地方的方法分解的情况。

图15：从一组的“蠕虫”形状的例子。

图16：在“虫”形状点的标签。

图17：点0,2,3,4，和6从对准组“蠕虫”的，与重叠平均形状的离散。

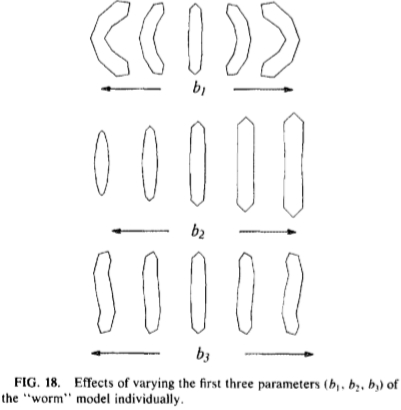
图18：单独改变“蠕虫”模型的前三个参数（b1，b2，b3）的影响。

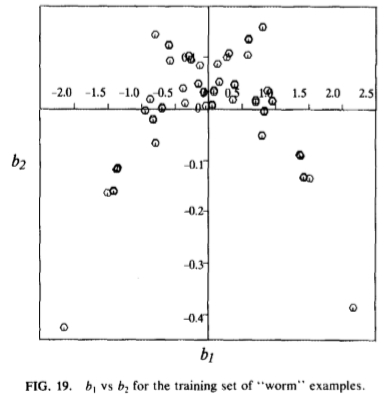
图19：b1 VS b2对于训练集的“虫”的实例。

在PDM每个变化模式移动沿直线地标点相对于局部坐标系。在一些情况下在一个类的形状的变化将通过沿曲线移动的点被更好地表示。弯曲或发生在类实例形状的相对旋转的效果时，这是特别重要的。考虑，例如，从图15所示的设定的设定的“蠕虫”的形状的实施例中由84种具有一个固定的宽度，但不同的曲率和长度人工产生的形状，每一个表示由12标记的点（图16）。图17显示了一些点的分散，一旦形状已对齐。一个变化的曲率导致点的形状形成弯曲云的端部。
 由标记的点的平均值的位置上形成的形状不具有恒定的宽度并且比训练形状的对准的版本更短。端点，0和6所示，形成弯曲的云，其中质心不撒谎云内。以这种方式产生的平均形状，因此不能充分地类似于固定，得到满意的模型训练。受过训练的有关此数据的PDM的变化的第一三种模式示于图18.在理想情况下一个期望的模型为具有一阶和二阶曲率作为其第一个两种模式。在PDM的第一模式是一个近似的弯曲，通过拟合直线，以点的弯曲的“云”而生成，所述第二模式给出必需的，因为线性近似是差的校正。该模型的第三模式提供了一个近似第二次弯曲，图19示出了前两个参数b1和b2之间的关系，虽然它们是线性独立的，明显有非线性关系存在。人们不能独立地选择的参数，并期望得到类似的在训练的形状集。我们讨论此途径可能在本文的最后克服这个问题。

4 使用点分布模型图像搜索中的 - 主动形状模型
其产生的弹性模型，我们想在图片搜索使用它们，找到图像建模对象的新实例。这涉及寻找形状和姿势，其导致模型与所述图像中的感兴趣结构相一致的参数。

该模型的实例由下式给出

为通过旋转和缩放s，和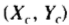
是在图像帧中的模型的中心的位置。
 在本节中，我们描述了发现给予了非常粗略的起点逼近适当的X迭代方法。希尔等人在别处遗传算法的搜索如何可以用来找到一个很好的起点逼近较快描述[26,7,27]。如果没有事先的兴趣对象的预期位置的知识，这是适用的。在实践中，X的起始值并不需要非常接近最终的解决方案，这样，对于许多实际应用，下面的方法可以单独使用。

迭代计划的想法是X的当前估计放入图像和检查各地各型号点图像的区域，以确定它移动到一个更好的位置移动。这些局部变形被转换成调整到PDM的姿态，比例和形状参数。通过执行所述形状参数的限制，全局形状约束可以应用于确保模型例的形状保持类似于训练集的。重复这个过程，直到没有显著变化导致。因为模型试图变形，但仅在与训练集中发现了形状一致的方式更好地适应数据，我们称他们为“主动形状模型”或“智能蛇”。

4.1 计算建议运动各种型号的点

图20：模型边界近似于边缘图像对象的一部分。

图21：点的建议的移动是沿垂直于边界，正比于最大边缘强度上正常。

鉴于我们正试图以适应我们需要找到一组将每个点移向一个更好的位置调整的图像对象一套示范点的位置的初始估计。当模型点表示对象的边界（图20），这涉及移动它们朝向图像边缘。有迹象表明，可以采取各种方法。在实施例中，我们描述我们下面使用调整沿着法线朝向最强图像边缘模型边界，具有大小正比于边缘（图21）的强度。
 另一种方法是，以产生潜在图像例如由Kass 等人[3]，可能的一个为每个模型点所描述的，描述所述图像中的每个点的似然性的模型点。调整每个点位置然后可以从电势图像的梯度在该点的位置的当前估计来导出。
 然而，它们获得，我们表示组调整（图22），其为矢量dX，为：

 

图22：调整到一组点。

4.2 计算变化的姿势和体形参数
我们的目标来调整模型的姿态和形状参数的点从在所述图像帧它们的当前的位置移动，X，以尽可能接近所建议的新位置（X + dX）作为可以同时仍满足形状被布置该模型的约束。如果模型的当前估计在与方向和规模s 居中，我们想先计算出如何更新这些参数，以更好地适应图像。这是通过找到翻译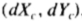，旋转和缩放使用中给出的比例因子（1 + ds），其最好的映射电流设定点，X，到集通过（X + dX）给定的点来实现 见附录A.
 调整了姿势变数仍然存在，只能通过模型​​的形状变形来满足剩余的调整。我们要计算的调整，dX，在使点 X通过 dX当新缩放，旋转和平移参数的影响相结合，移动所需的局部坐标系。
 在图像帧的点的初始位置由方程（17）给出，

 

我们要计算一组剩余的调整dX的局部模型坐标系，使得

 

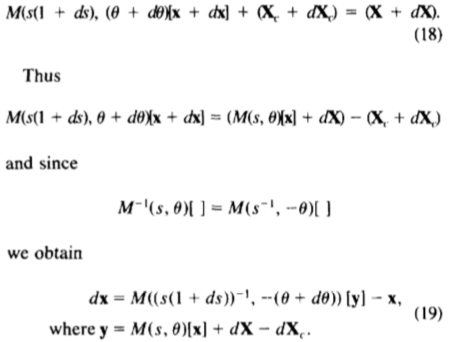
等式（19）给出计算所建议的动作来在点 X在局部模型坐标框架的方法。这些运动都是不符合我们的形状模型一般是一致的。为了应用形状限制，我们改造成 dX模型参数空间，让分贝的变化越紧密调整模型指向 dX为允许所需的模型参数。

 

由于只有 t（<2n）可用的变化和 dx 可以2n 个不同自由度移动的点的方式，我们只能实现的近似所需的变形。
 减法（14）由（20）给出

 

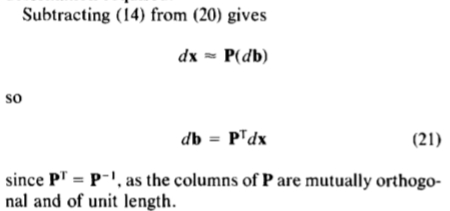
由于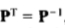，为P的列是相互正交单元长度的和。
 可以示出的是方程（21）等效于使用最小二乘近似来计算形状参数的调整，db。
 

4.3 更新姿势和体形参数
上述等式让我们来计算改变姿势变量和调整，，该形状参数 db 需要改善的对象模型和图像证据之间的匹配。我们将这些以迭代计划更新参数，

 

其中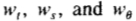为标量权重，Wb，是权重对角矩阵，一个用于每个模式。这可以是身份，或每重量可以正比于在所述训练集合中的相应的形状参数的标准偏差。后者允许在存在倾向较大形状的变化模式的更多快速移动。我们可以保证的是，模型只变形为形状与放置在BK的值限制设置的培训是一致的。如果Mahalanobis马氏距离小于合适的常数，的形状可以被认为是可接受的，说3.0（参见方程（16））。此限制是计算，使得几乎所有的训练样例满足方程（16）。

向量b应在关于原点超椭圆之内。如果更新使用b（26）导致不可信的形状，即，和点位于椭圆体以外，b cat：被重新缩放趴在允许量的最近点使用

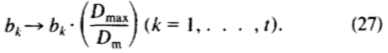
请注意，我们已申请的零隐含限制从我们表示截断的特征向量的权重（即，）。一旦已更新参数，并且施加限制在必要时，所述模型点的更新位置可以被计算，并且导出每个点新建议的动作。重复这个过程，直到没有显著变化的结果。

 4.4 示例使用主动形状模型
上述技术已在许多应用中，工业和医疗[26,27,33]成功应用。在这里，我们将介绍使用电阻器，心脏和手上述模型的结果。
 在每一种情况下的位置，方向和比例的初始估计被制成，并且所述主动形状模型（ASM）的形状参数在零被初始化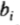（=）。每个模型点建议运动通过找到沿着垂直于边界最强边缘（正确的极性的）在点（参见4.1和图21）来计算。调整参数被计算和应用，并且重复该过程。

4.4.1 定位电阻器
我们已经构建了电阻器的点分布模型，使用32个点（第3.4.1节），表示它的边界。图23示出的叠加，它朝向所述图像中的组件迭代电阻边界模型的印刷电路板的一部分的图像。我们内插一个额外的32个点，每一个双模型点的边界周围之间，并且通过寻找最强边缘计算调整每个点沿型材20个像素在每个点长居中。我们利用5个自由度的形状模型。在ASM的每次迭代呈现在Sun SPARC 10工作站大约0.015s。
 该方法有效地保持模型的全局形状约束和效果很好，给出一个足够好的开始逼近；我们将讨论在其他地方[26,27]获得这样的初始假设的方法。
 

图23：印刷电路板的叠加电阻模型，示出了它的初始位置，并且在30，60,90和120次的迭代其位置部分。

4.4.2 定位心室
图24a示出了超声心动图的一个例子。左心室是在成像区域的右上角。图24b示出了上述96点心脏腔室模型（第3.4.2节）的一个实例的初始放置。图24c示出了后80次迭代的ASM。后200次迭代（图24D）的模型提供了良好的拟合到数据。所用的形状模型具有12个自由度。到每个点的调整使用在平滑化图像的最强边缘沿轮廓40个像素长中心的点计算的。每个ASM迭代需要在Sun SPARC 10 工作站大约 0.03S。在这个例子中该模型能够推断的边界的地方有通过使用预期形状的信息从图像，其中的区域组合的知识缺失的数据（例如，心室的顶部）的部分的位置对于室壁很好的证据都可以找到。如果没有通过模型给出的形状的先验知识就不可能准确地划定边界心室。该方法的进一步的医疗应用在[33]中描述。

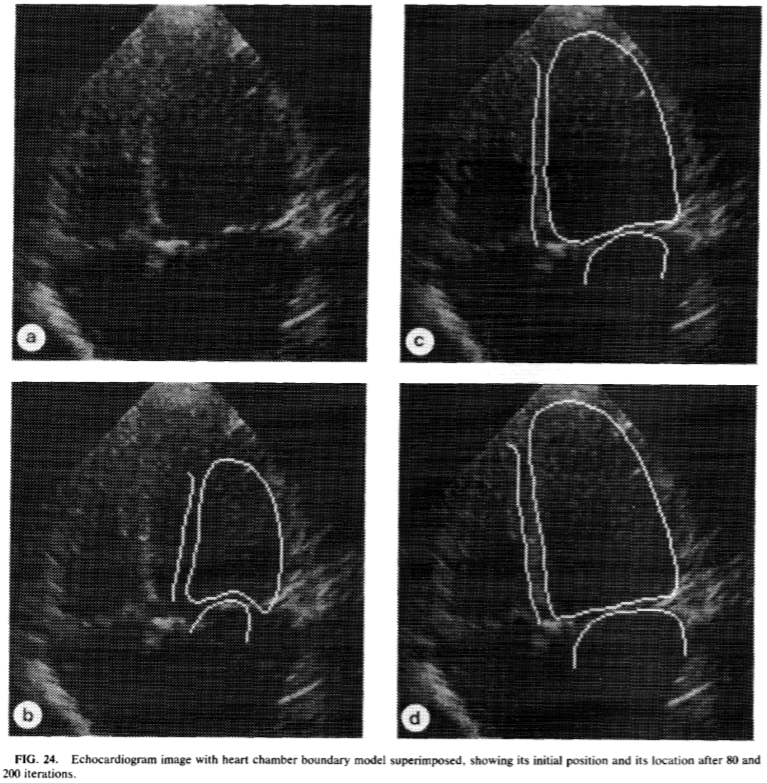
图24：具有叠加心脏腔室边界模型，示出了它的初始位置，并且80和200次迭代后其位置超声心动图图像。

 4.4.3 定位手
我们已经构建了手的点分布模型，表示使用72点（第3.4.3节）的边界。图25显示了一些之中杂波和闭塞，并且模型朝它迭代的例子笔者的一只手的形象。我们通过寻找在轮廓35个像素长集中在一点上最强的边缘计算调整每个点。形状模型具有8个自由度，并且每个迭代ASM需要约0.02秒在Sun SPARC 10 工作站。结果表明，该方法能够处理混乱和有限的闭塞。

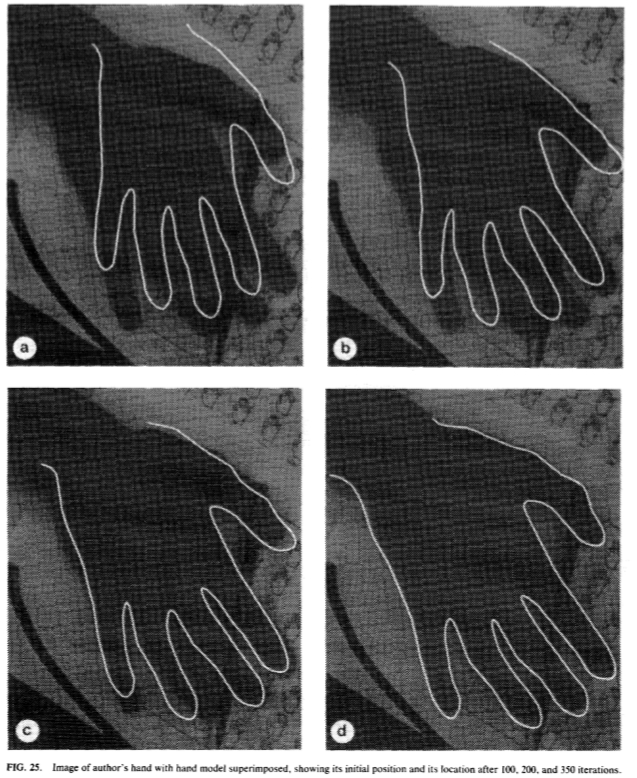
图25：作者的手模型手叠加，显示出其初始位置，之后100，200和350次的迭代的位置的图像。

5.讨论
以上的例子说明了我们的方法的主要特点。使用单一的方法，只能由具有一套合适的例子培训专业，我们已经能够自动定位在复杂的，嘈杂的，和杂乱的图像一系列结构。另有报道其它实例包括面[36]，手写字符[36]，解剖结构在脑和腹部[33]的磁共振图像，椎骨在X光片[33]，在压力图像脚的部分[38]和所有在汽车制动器组件的部件[34]。我们下面讨论一些这项工作，包括在需要进一步发展的领域，其出现的问题。
 

5.1 点分布模型
5.1.1 示范点和训练例子的选择
这是很重要的标志点尽可能精确放置在训练图像成为可能。如果点是不是在每个形状的正确位置，该模型将无法正确表示的位置点，将包括描述由在点位置误差的噪声项。它安排的是用于训练模型中的所有实施例被类似地相对于对准来设置轴的，以确保在不同形状的标记的点被正确相比是同样重要的。在某些情况下一个明显取向是明显的，但在其他，特别是医疗例子，其中器官的形状是非常灵活的，自动最小二乘对准方法是必不可少的。
 当然，将手的每一点每一训练图像上可以非常耗时。我们正在开发工具，以减轻该过程。技术，诸如那些由Burr [29]和 Sclaroff和Pentland [30]的有限元模型或 Nastar和Ayache [21]中描述的可能能够帮助用户在该训练阶段定位点对应。
 在一些情况下闭塞和噪声将导致在一些点不能准确地定位图像。是简单的调整平均形状的计算（7）和协方差矩阵（9），得到一个加权，以在训练集中的每一个例子中，每个点当某些点缺失，对于已知点的权重可以被设置为统一的；那些未知点可以被设置为零。只要点只有一小部分缺少任何一个例子，也没有点是从所有的例子丢失，仍然可以建立有用的模型。
 原则上可能的“训练过度”的典范。假设的例子大的比例分别为接近均值和当时只有一个或两个例子表明形状变化的一些具体形式。可能的是，当要使用的模式的数目，T，被选择，最能说明不频繁的形状变化的模式将被截断，因为它仅说明了总方差的量小。然而，由于训练实例通常被选择并用手标记，这是耗时且低效的，包括了许多类似的形状，最好是选择各种其覆盖整个范围的变化的一个容易观察不同的形状的（其中如可用）。正是在这个阶段，人的专业知识能够发挥作用。
 

5.1.2 多模式
该心脏的例子说明了一个重要事实——即用于构建一个PDM及其派生ASM点不需要属于单个对象或形状。一个点的连接是不相关的PDM的结构，并且仅用于由ASM以确定在图像搜索期间的每个点的局部法线的方向。复杂的组件的多个子部分以及它们之间的空间关系的形状可以因此通过一个单一的PDM表示。以统一的方式处理的形状和空间关系一个显著优点是子组件的位置和形状之间的相关性可以被建模；这是重要的，例如，在相互关联的机械部件的组件或在几个器官“打包”到同一腔医用图像。

5.1.3 模型形状变化
我们发现在3.3节，每个排列形状可以被看作成2n 维空间中的一个点，而整个训练设定点在这个空间云。我们尝试使用容许形状域的想法这个云模型。对于搜索的方法来有效地解决它，这个域名是简单的连接是非常重要的，而且我们有大约域航行的简单方法。假设域是椭圆形（或同一轴线一箱）使我们能够做到这一点。然而，在某些情况下，这是不恰当的模型。当有一个很大程度的弯曲或训练集中的相对旋转，地标之间的非线性关系可以给在2*n 维空间中的云“香蕉”形或更糟。在这种情况下，如第3.4.4证实，椭圆形的假设给出了一个形状模型时，与训练组相比，它可以产生严重的扭曲的形状。该模型是不具体的人会喜欢，只有它才能产生形状的子集就被认为是“合法的”。在某些情况下，这不是灾难性的。例如，鉴于蠕虫模型可以成功地用于定位图像蠕虫的例子，但该模型是由噪声或杂波比一个更具体的模型将被扭曲更敏感。
 允许的形状域的更一般的模型可能会导致更具体的形状模型。我们采用多项式，而不是直线试验，域的结果令人鼓舞。代替每个模式定义对于每个点的直线运动的，这些点遵循多项式曲线作为参数而变化。结果将在进一步的论文中呈现。

 5.1.4 用例的小数字处理
如果有训练实例更少，N，比点坐标（2n），这是常有的情况下，特别是对于复杂的模型，可以有不超过在模型中的N-1个自由度的更多。所述方法所需的主成分分析使用     2n* 2n 个矩阵S 的特征向量（方程9,10）。当N <2n 个该矩阵具有不超过N-1 的非零特征值以上。在这种情况下，计算所有的2n 特征向量是不必要的。计算与非零本征值相关联的特征向量的一种有效方式是在附录B中给出。

5.1.5 扩展模型
而不是具有表示复杂的装配一个“平面” PDM，有可能建立在其中顶层控制之下的层的位置，比例，方向和形状参数的分层PDM。底层可以由多个子组件，每一个由“平坦” PDM表示。改变顶层的参数而变化的姿态，尺度，和下面的各种部件的形状，这避免了与PDM由于旋转的问题的子组件——它们相对于组件的其余部分取向可以显式地进行建模，而不是隐式地在一个单层线性PDM。
 这也很容易扩展点分布模型来处理三维数据，例如，三维医学图像。最近，我们描述了一个成功的系统使用3D PDM [35]大脑的三维磁共振图像的自动解释。
 

5.1.6 弦长分布
别处我们已经描述如何导出从训练集使用双点 - 的弦长分布模型[31]之间的距离的形状模型。一个距离，，每对 i，j 在训练集中的每个实施例中的计算点，并且这些弦长变化的方式之间是通过计算它们的平均和协方差和施加主成分分析建模。获得了具有若干参数的模型，它返回集中心点的距离，，从中可以构造一个新的形状。改变参数而变化的距离，这导致形状发生变化。这样的系统能够不管到物体的刚性部件建模它们的取向，因为它仅依赖于内部的距离。虽然这种技术是在表示可以弯曲对象（如比线性PDM有时更好的“蠕虫”），从点之间的距离的形状的重建是迭代的和缓慢的。使用这种模型的细化技术是复杂的，导致我们倾向于实际应用的PDM。
 

5.1.7 使用的分类
一个PDM也可以在一个分类器中使用。给定的形状的一个例子，估计可以由该示例是如何可能是类通过模型描述的形状的构件。如果标记的点被放置在例如与点集与平均形状对齐，我们可以计算出以产生示例所需的模型参数。参数的分布可以从训练集中估计，从而允许被分配的概率。或者，在图像未知对象的分类可以通过训练模型被认为是每一类制成。给定一个新的图像，则ASM技术被用来以适应每个模型到图像数据。给出最佳拟合到图像中的一个被选择作为结果[36]。

5.2 使用的图像置搜索的PDM

我们已经表明，ASM的是在给定的位置，规模和方向的初步估计图像定位已知对象的有效。如何更好的按需要的估计将取决于图像如何混乱，以及如何很好的模型描述了图像中的物体。举例来说，除非模型中的一些点足够接近了他们的搜索曲线重叠的目标对象上相应的边缘的图像。例如，模型实例不能“看到”的目标，并不能朝目标迈进。我们已经发现，使用遗传算法技术[26,7,27]提供适当的接近初步估计，实现与ASM的成功细化。
 

5.2.1 闭塞和杂波
手的例子表明，ASM的可与闭塞和杂波成功应对。该心脏例子也表明，该方法可与噪声图像和丢失的数据。至于噪音，混乱和闭塞增加很有可能成为现实，该车型将含住了错误的边缘，虽然由PDM应用的约束保证最终结果的形状是“明智的”，即使它没有找到所有边缘正确。这是最有可能发生的杂波具有相似的结构，以使各对象建模，因此最有可能被误认为是对象的某些部分发生。由于我们使用的车型是具体的，我们认为我们正在申请最强烈的基于形状的限制。在极端情况下，如果该方法失败，故障出在我们的方法来整合证据——这是下面讨论的图像。

 5.2.2 更新模型参数
建议调整是如何发现每个点是很重要的。通过寻找强大的计算表明运动附近的边缘是简单的，并已证明是有效的在许多情况下。然而，寻找更复杂的对象，其中示范点不一定趴在强边缘，需要更复杂的算法。潜在的地图可以源自，描述图像，这是一个特定模型点在每个点的可能性。在搜索每个模型点试图转向更可能的位置，在势图爬坡。可替代地，可以从训练实例来产生围绕每一个模型点的预期灰度等级的模型；图像搜索中的每个点，然后向其中最好的局部灰度模式相匹配的附近区域移动。使用后一种技术的实验已表明，它是更灵活，不是简单地搜索强边缘[32,34]对噪声和杂波较不敏感。
 通过允许模型变形，但只有在训练集中看到的方式，我们有细化的强大技术。对模型的形状的约束由在形状参数的限制施加。变化中的 2n-t 未示出的模式有效地对它们的参数的零限制。而不是固定的限制被用于执行形状的限制，在参数空间恢复力可以应用于从图像拉动参数回零抵抗外部“力”；

 

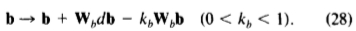
这将为解决方案给予更大权重接近均值形状，并且需要为此得到了较大变形形状的有力证据。然而，因为这将有可能导致图像数据和模型之间的折中解决方案，我们看好固定限制的做法。

 5.2.3 与其他作业相比，
我们在座的工作可以看作是 Lowe 的细化技术[37]的二维应用。由于点分布模型的线性性质的，数学是相当简单，导致快速执行。
 我们主动形状模型是表面上类似于主动轮廓模型（Snakes）和有限元模型（FEMs 前端模块）。每个都有各自的优点。Snakes和FEMs 前端模块可以创建相对容易，并有在嘈杂，混乱的场面定位部分遮挡物体的能力。这些模型都没有，但是，很具体，所以困难的条件下，他们可以产生令人难以置信的解释。一个ASM是很难创建，因为它们需要用户用正确的解释标注每一个训练图像集组成。然而，他们所允许的变异性更具体地进行建模，并因此对噪声更鲁棒，杂波，和闭塞。 ASM和有限元方法之间详细的实验比较超出了本文的范围，但我们希望在不久的将来呈现的结果。我们也正在积极在其上结合了这两种方法的优点的方法。

 5.2.4一种对象建模和识别框架
我们已经进行了实验，这表明，我们的局部优化方法可以结合卓有成效使用遗传算法（GA）搜索[26-28]。该GA可以作为一个线索发电机以产生一个数字对象的假设的，这可以使用主动形状模型细化运行。可替代地，ASM可与GA的搜索相组合，在遗传算法的每一代施加一个迭代。这两种技术已成功用于定位在各种图像的复杂结构。

6 结论
我们已经描述了点分布模型（PDMs），它可以从训练集正确地标记的图像的构造形状的——统计模型。一个PDM表示对象作为一组标记点的，给出了它们的平均位置和一小的变化的模式的其中描述对象的形状如何变化。运用限制模型的参数强制全局形状约束确保所产生的任何新的例子是类似的训练集。给定一组形状参数，模型的实例可快速计算。该机型结构紧凑，非常适合于产生和测试图片搜索战略。

主动形状模型（ASMs）利用在能够快速定位的模型化的结构在噪声，杂乱图像 - 即使它们是部分闭塞的迭代搜索过程 PDMs 的线性公式。对象识别和定位是稳健的，因为这些模型是特异性的，因为实例约束为相似的训练集中的感觉。
 我们已经证明了创造电阻，心（在超声心动图），和手的紧凑车型的能力。我们还表明，这些模型能够成功地在图片搜索中使用。使用常规的工作站通常可以在几秒钟内获得良好的解释。我们已经描述，其中相同的方法已经成功地利用别处各种其它应用，包括在非常复杂的结构（例如，脸和汽车制动器组件）被建模的例子。重要的一点强调的是，正是相同的软件可以被应用于广泛的图像判读问题，医疗和仅通过训练用合适的例子工业专业。
 我们认为，这种做法持有相当大的希望，作为自动图像演绎实用，通用技术。

附录A：对齐一对形状
给定两个类似形状，x1 和 x2，我们想选择的旋转，缩放s，一个翻译，映射x2 到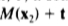，从而加权，以尽量减少和

和 W 是每个点的权重的对角矩阵。如果我们写

最小二乘法（相对于每个变量进行微分）导致一组四个线性方程。

这些可以使用标准矩阵方法针对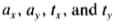求解。

附录B：计算的协方差矩阵的特征向量时，有较少的样本比坐标
当有训练实例更少，N，比点坐标，2N的2N×2N的协方差矩阵S的本征向量可被来自相同数据得到的较小的N * N矩阵的特征向量计算的。因为特征向量计算时间是矩阵大小的立方，所以这可以节省大量时间。
我们有N个例子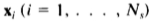，。 设D为2n×N矩阵，以列为列;

我们可以将协方差矩阵S写为


设T为N×N矩阵

并且让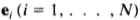为T的单位，正交特征向量与对应的特征值：

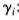预乘D，

因此，如果是T的特征向量，那么，是S的特征向量并且具有相同的特征值。 然后，S的N个单位正交特征向量是

具有相应的特征值。需要等式42中的缩放因子来给出特征向量单位长度。 相互正交很容易显示出来：

致谢
这项工作是由下信息工程先进技术计划的科学与工程研究理事会的资助。（项目编号2114分之3）Tim Cootes目前由电监会博士后奖学金资助。作者感谢Wolfson 的图像分析单元的其他成员特别 D.Bailes 和A·Hill ，对他们的帮助和建议，并为他们的建议匿名评审。

参考文献

1.R.T.Chin and C.R.Dyer,Model-based recognition in robot vision, Comput.Suru.18,1986,67-108.
2.W.E.L.Grimson,Object Recognition by Computer:The Role of Geometric Constraints,MIT Press,Cambridge,MA,1990.
3.M.Kass,A.Witkin,and D.Terzopoulos.Snakes:Active contour models,in Proceedings,Firt International Conference on Conmputer Vision,pp.259-268,IEEE Comput.Soc.Press,1987.
4.GEHinton,CKIWilliams,and MDRevow,Adaptive elastic models for hand-printed character recognition,in Aduances in Nelural Information Processing Systems 4(JEMoody,SJHanson, and RPLippmann,Eds.),Morgan Kauffmann,San Mateo,CA, 1992.
5.A.L.Yuille,D.S.Cohen,and P.Hallinan,Feature extraction from faces using deformable templates,Int.J.Comput.Vision 8,1992, 99-112.
6.P.Lipson,ALYuille,D.O'Keeffe,J.Cavanaugh,J.Taaffe,and D.Rosenthal,Deformable templates for feature extraction from medical images,in Proceedings of the First European Conference on Computer Vision(O. Faugeras,Ed.),Lecture Notes in Computer Science,pp.413-417,Springer-Verlag,Berlin/New York,1990.
7.A.Hill and C.J.Taylor,Model based image interpretation using genetic algorithms,Image Vision Comput.10,1992,295-300.
8.A.Beinglass and H.J.Wolfson,Articulated object recognition,or: How to generalize the generalized Hough transform in Proceedings, IEEE Computer Society Conference on Computer Vision and Pal tern Recognition 1991,pp.461-466.

9.G.L.Scott,The alternative Snake--And other animals,in Proceedings,3rd Aluey Vision Conference.Cambridge,1987,pp.341-347.
10.L.H.Staib and J.S.Duncan,Parametrically deformable contour  models,in IEEE Computer Society Conference on Computer Vision  and Pattern Recognition,San Diego,1989,pp.427-430.
11.H.1.Bozma and J.S.Duncan,Model-based recognition of multiple  deformable objects using a game-theoretic framework,in Information Processing in Medical lmaging-Proceedings of the 12th International Conference,pp.358-372,Springer-Verlag,Berlin/New  York,1991.
12.U.Grenander,Y.Chow,and D.M.Keenan,Hands.A Pattern  Theoretic Study of Biological Shapes,Springer-Verlag,New York,  1991.
13.U.Grenander and M.1.Miller,Representations of knowledge in  complex systems.J.R.Stat.Soc.B,in press.
14.C.Goodall,Procrustes methods in the statistical analysis of shape  (with discussions),J.R.Stat.Soc.B.53,1991,285-339.
15.K.V.Mardia,J.T.Kent,and A.N.Walder,Statistical shape  models in image analysis,in Proceedings of the 23rd Symposium  on the Interface,Seattle 1991,pp.550-557.
16.F.L.Bookstein,Morphometric Tools for Landmark Data,Cambridge Univ.Press,London/New York,199l.
17.F.L.Bookstein,Principal warps:Thin-plate splines and the decomposition of deformations,IEEE Trans.Pattern Anal.Mach.Intell.11，1989，567-585.
18.A.Pentland,Automatic extraction of deformable part models,Int. J.Comput.Vision 13,No.2,1990,107-126.

19.A.Pentland and S.Sclaroff,Closed-form solutions for physically  based modeling and recognition,IEEE Trans.Pattern Anal.Mach.Intell.13,1991,715-729.
20.D.Terzopoulos and D.Metaxas,Dynamic 3D models with local  and global deformations:Deformable superquadrics,IEEE Trans.Pattern Anal.Mach.Intell.13,1991,703-714.
21.C.Nastar and N.Ayache,Fast segmentation,tracking and analysis  of deformable objects,in Proceedings,International Conference  on Computer Vision,1993,pp.275-279,IEEE Comput.Soc.Press,  1993.
22.P.Karaolani,G.D.Sullivan,K.D.Baker,and M.J.Baines.A  finite element method for deformable models,in Proceedings of the  Fifth Aluey Vision Conference,Reading,/989,pp.73-78.
23.P.Karaolani,G.D.Sullivan,and K.D.Baker,Active contours  using finite elements to control local scale,in Proceedings,British  Machine Vision Conference 1992,pp.481-487,Springer-Verlag.Berlin/New York,1992.
24.J.C.Gower,Generalized Procrustes analysis,Psychometrika 40,  1975,33-51.
25.R.A.Johnson and D.W.Wichern,Multivariate Statistics,A Practical Approach,Chapman & Hall,London/New York,1988.
26.A.Hill,T.F.Cootes,and C.J.Taylor,A genetic system for image  interpretation using flexible templates,in British Machine Vision  Conference,Springer-Verlag,1992.
27.A.Hill,C.J.Taylor,and T.Cootes,Object recognition by flexible  template matching using genetic algorithms,in Proceedings,European Conference on Computer Vision (G.Sandini,Ed.),pp.852-856,Springer-Verlag,Berlin/New York,1992.
28.A.Hill,A.Thornham,and C.J.Taylor,Model-based interpretation  of 3D medical images,in Proceedings,British Machine Vision Conference 1993(J.llingworth,Ed.),Vol.2,pp.339-348,BMVA  Press,1993.

29.D.J.Burr,A dynamic model for image registration,Comput.Graphics lmage Process.15,1981,pp.102-l12.

30.S.Sclaroffand A.Pentland,A model framework for correspondence  and description,in Proceedings,International Conference on Computer Vision,1993,pp.715-729,IEEE Comput.Soc.Press,(993.
31.T.F.Cootes,D.H.Cooper,C.J.Taylor,and J.Graham.A trainable  method of parametric shape description,Image Vision Comput.10,  1992,289-294.
32.T.F.Cootes and C.J.Taylor.Active shape model search using  local grey-level models:A quantitative evaluation,in Proceedings.British Machine Vision Conference 1993(J.llingworth,Ed.),Vol.2，pp.639-648，BMVA Press,1993.
33.T.F.Cootes,A.Hill,C.J.Taylor,and J.Haslam,The use of  active shape models for locating structures in medical images,in  Proceedings,Information Processing for Medical Imaging (H.H.Barrett and A.F.Gmitro,Ed.),pp.33-47.Springer-Verlag.Berlin/  New York,1993.
34.T.F.Cootes,C.J.Taylor,A.Lanitis,D.H.Cooper,and J.Graham.Building and using flexible models incorporating grey-level information,in Proceedings,International Conference on Computer Vision.pp.242-246,IEEE Comput.Soc.Press,1993.
35.A.Hill,A.Thornham,and C.J.Taylor,Model-based interpretation  of 3D medical images,in Proceedings,British Machine Vision Conference,1993(J.llingworth,Ed.), Vol.1.pp.339-348,BMVA  Press,1993.
36.A.Lanitis,C.J.Taylor,and T.F.Cootes,A generic system for  classifying variable objects using flexible template matching,in Proceedings,British Machine Vision Conference,1993(J.llingworth.Ed.),Vol.l,pp.329-338,BMVA Press,1993.
37.D.G.Lowe,Fitting parameterized three-dimensional models to  images,IEEE Trans.Pattern Anal.Mach.Intell.13,1991,441-450.
38.J.A.Grogan,Automated Analysis of Pedobarograph Images.M.Sc.Thesis,Victoria University of Manchester.Oct.1993.