Codeforces Round #634 (Div 3) 题解

A Candies and Two Sisters

题目链接

没有什么好说的，直接上代码：

 #include <iostream> 
 #include <cstdio>
 #include <cstring>
 using namespace std;
 
 int T, n;
 
 int main()
 {
     scanf("%d", &T);
     while(T--)
     {
         scanf("%d", &n);
         if(n <= 2) printf("0
");
         else 
         {
             if(n & 1) printf("%d
", n / 2);
             else printf("%d
", n / 2 - 1);
         }
     }
     return 0;
 }

B Construct the String

题目链接

因为我们只关心字符的种类数，不关心其顺序。可以想象一个大小为 a 的窗口，从左到右滑过整个字符串。

前 a 个格子用 b 种字符随便构造。窗口每往后滑一次，就有一个新格子进入窗口，一个旧格子离开窗口。只要让新格子=旧格子，该窗口内的字符种类数将不会改变。

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 using namespace std;
 
 int T, n, a, b, ans[4002];
 
 int main()
 {
     scanf("%d", &T);
     while(T--)
     {
         scanf("%d%d%d", &n, &a, &b);
         for(int i = 1; i <= a - b + 1; i++) ans[i] = 1;
         for(int i = a - b + 2; i <= a; i++) ans[i] = ans[i - 1] + 1;
         for(int i = a + 1; i <= n; i++) ans[i] = ans[i - a];
         for(int i = 1; i <= n; i++) cout << (char)(ans[i] + 96);
         printf("
");
     }
     return 0;
 }

C Two Teams Composing

题目链接

先统计出一共有多少种技能，记为 (num)，再统计出出现最多的技能的出现次数，记为 (max)。

如果 (num < max)，最好的方案是 A 队选择所有种类的技能，此时 B 队在也一定能有相同数量的人符合条件

如果 (num > max)，最好的方案是 B 队选择 (max) 个出现最多的技能，此时 A 队在除去该技能的情况下，仍然有足够多的人数符合条件

如果 (num = max)，注意，如果 B 队选择 (max) 个出现最多的技能，这一种技能已经被全部用完，A 队不能选择该技能，此时 A 队的人数就会变成 B 队的人数 (-1)，这时不符合条件的。所以这种情况的最大答案是 (num(max)-1)

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 using namespace std;
 
 int T, n, a, vis[500002], num, max_;
 
 int main()
 {
     scanf("%d", &T);
     while(T--)
     {
         scanf("%d", &n);
         num = max_ = 0;
         memset(vis, 0, sizeof(vis));
         for(int i = 1; i <= n; i++)
         {
             scanf("%d", &a);
             vis[a]++; if(vis[a] == 1) num++;
             max_ = max(max_, vis[a]);
         }
         if(num != max_) printf("%d
", min(num, max_));
         else printf("%d
", max_ - 1);
     }
     return 0;
 }

D Anti-Sudoku

题目链接

抄样例的好题。正解就是样例改哪个位置你就改哪个位置，至于改成什么并不重要，只要是跟原来不一样的就行。

 #include <iostream>
 #include <cstdio>
 #include <algorithm>
 #include <algorithm>
 using namespace std;
 
 int T, a[12][12];
 char c;
 
 int ch(int x, int y)
 {
     int now = a[x][y] + 1;
     if(now == 10) now = 1;
     a[x][y] = now;
 }
 
 int main()
 {
     scanf("%d", &T);
     while(T--)
     {
         for(int i = 1; i <= 9; i++)
             for(int j = 1; j <= 9; j++)
             {
                 cin >> c;
                 a[i][j] = c - '0';
             }
         ch(1, 7), ch(2, 2), ch(3, 6);
         ch(4, 9), ch(5, 3), ch(6, 5);
         ch(7, 8), ch(8, 1), ch(9, 4);
         for(int i = 1; i <= 9; i++)
         {
             for(int j = 1; j <= 9; j++) printf("%d", a[i][j]);
             printf("
");
         }
     }
     return 0;
 }

E1 Three Blocks Palindrome (easy version)

题目链接

这一题跟下一题除了数据范围都是一样的。不过从这一题开始想比较简单。

题目要求分为 (X/Y/X) 三部分，其中对 (Y) 的大小没有要求，而两边的 (X) 数量必须一致。(a_i) 的范围很小，考虑从这里入手。

假设我们现在已经选择了 (X = a)，为了保证解的最优性，回文串的最左边应选择 数列中出现的第一个 a，最右边应选择 数列中出现的最后一个 a。

设 (mode(l,r)) 表示 ([l,r]) 的众数出现次数。若只选择最左边和最右边的两个 (a)，此时回文串的最大长度 = (2 + mode(pos_{start}+1,pos_{end}-1))。而所有的 (mode(l,r)) 都可以在预处理中 (O(n^2)) 的处理出来。

接下来把第一段和第三段的长度都增加到 (2)，只要加入从左数第二个 (a)，和从右数第二个 (a) 即可。同样，每个位置的前一个 / 后一个与其值相同的位置也可以通过预处理 (O(n)) 得出。

这一过程每个位置只会被遍历到 (1) 次，复杂度为 (O(n))。加入预处理后总复杂度为 (O(n^2))

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 using namespace std;
 
 const int N = 3002;
 int T, n, a[N], num[50], f[2004][2004], l[N], lst[N];
 int r[N], nxt[N], vis[N], st[N], ed[N], ans;
 
 int main()
 {
     scanf("%d", &T);
     while(T--)
     {
         scanf("%d", &n); ans = 1;
         memset(lst, 0, sizeof(lst));
         memset(nxt, 0, sizeof(nxt));
         memset(vis, 0, sizeof(vis));
         memset(f, 0, sizeof(f));
         for(int i = 1; i <= n; i++)
         {
             scanf("%d", &a[i]);
             if(!lst[a[i]]) st[a[i]] = i;
             l[i] = lst[a[i]]; lst[a[i]] = i;
         }
         for(int i = n; i >= 1; i--)
         {
             if(!nxt[a[i]]) ed[a[i]] = i;
             r[i] = nxt[a[i]]; nxt[a[i]] = i;
         }
         for(int i = 1; i <= n; i++)
         {
             for(int j = i; j <= n; j++)
             {
                 num[a[j]]++;
                 f[i][j] = max(f[i][j - 1], num[a[j]]);
             }
             for(int j = i; j <= n; j++) num[a[j]] = 0;
         }
         for(int i = 1; i <= n; i++)
         {
             int x = a[i], L = st[x], R = ed[x], tot = 1;
             if(!vis[x])
             {
                 vis[x] = 1;
                 while(L < R)
                 {
                     ans = max(ans, tot * 2 + f[L + 1][R - 1]);
                     tot++; L = r[L], R = l[R];
                 }
             }
         }
         printf("%d
", ans);
     }
     return 0;
 }

E2 Three Blocks Palindrome (hard version)

题目链接

数据范围增大，需要一个 (O()(cnt_{ai})(n)) 的做法。

那么 (E1) 的做法能不能优化呢？答案是可以的。(E1) 做法的复杂度高在预处理上，只能直接把计算 (mode(l,r)) 放在枚举 (a_i) 的循环里，暴力肯定是不行了。现在的任务变成了，如何由 (mode(l,r)) 推出 (mode(nxt_l,pre_r))，范围减小了，很难操作。不妨把枚举的顺序倒过来，从小范围推出大范围。

例如，原来在 (E1) 中（如图），我们做的是由 (l,r) 变为 (nxtl,prer)，(Y) 的范围由大变小；现在我们把它反过来。

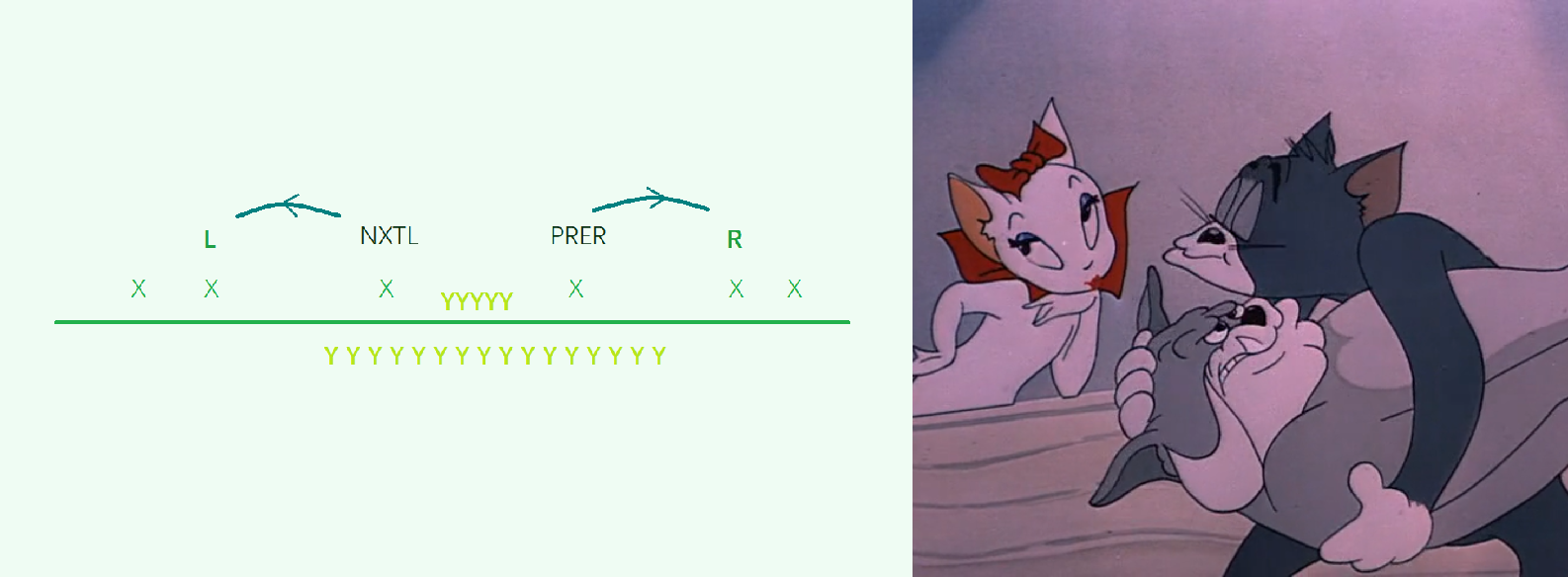
这样一来 (mode(l,r)) 好处理多了，只要把新增的元素加进去，顺便与原来的最大次数取最大值。在每个 (a_i) 的循环里，每个位置只会遍历到 (1) 次，所以总复杂度就是 (O()(cnt_{ai})(n))。

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 using namespace std;
 
 const int N = 300000, M = 250;
 int T, n, tot[M], a[N], num[M], lst[M], nxt[M], l[N], r[N];
 int st[M], ed[M], vis[M], max_, ans;
 
 int getmode(int x, int y)
 {
     int res = 0;
     memset(tot, 0, sizeof(tot));
     for(int i = x; i <= y; i++)
     {
         tot[a[i]]++;
         res = max(res, tot[a[i]]);
     }
     return res;
 }
 
 int main()
 {
     scanf("%d", &T);
     while(T--)
     {
         scanf("%d", &n); ans = 1;
         memset(num, 0, sizeof(num));
         memset(lst, 0, sizeof(lst));
         memset(nxt, 0, sizeof(nxt));
         memset(st, 0, sizeof(st));
         memset(ed, 0, sizeof(ed));
         for(int i = 1; i <= n; i++)
             scanf("%d", &a[i]), num[a[i]]++;
         memset(tot, 0, sizeof(tot));
         for(int i = 1; i <= n; i++)
         {
             l[i] = lst[a[i]]; lst[a[i]] = i;
             tot[a[i]]++;
             if(tot[a[i]] == num[a[i]] / 2) st[a[i]] = i;
         }
         memset(tot, 0, sizeof(tot));
         for(int i = n; i > 0; i--)
         {
             r[i] = nxt[a[i]]; nxt[a[i]] = i;
             tot[a[i]]++;
             if(tot[a[i]] == num[a[i]] / 2) ed[a[i]] = i;
         }
         memset(vis, 0, sizeof(vis));
         for(int i = 1; i <= n; i++)
         {
             if(!vis[a[i]] && num[a[i]] > 1)
             {
                 vis[a[i]] = 1;
                 int x = a[i], L = st[x], R = ed[x], cnt; 
                 max_ = getmode(L + 1, R - 1);
                 cnt = (num[x] / 2) * 2;
                 ans = max(ans, max_ + cnt);
                 while(l[L] != 0 && r[R] != 0)
                 {
                     cnt -= 2;
                     for(int j = L; j >= l[L] + 1; j--)
                     {
                         tot[a[j]]++;
                         max_ = max(max_, tot[a[j]]);
                     }
                     for(int j = R; j <= r[R] - 1; j++)
                     {
                         tot[a[j]]++;
                         max_ = max(max_, tot[a[j]]);
                     }
                     L = l[L], R = r[R];
                     ans = max(ans, max_ + cnt);
                 }
             }
         }
         printf("%d
", ans);    
     }
     return 0;
 }

F Robots on a Grid

题目链接

开局提示：千万不要在每组数据里面 memset。

首先，观察到题面一句话：让机器人无限次的行走。简单来说，要想让机器人无限次行走，每个格点按照行走方向连有向边（不必真的连），图中一定存在至少一个环。所有的点据此可以分为两类：本来就在环上；走几步也能到环上。每个环和周围的路径看起来就像这样：

还有几条显而易见的事实：

(1.) 由于每个点只有一条出边：任何两个环都不会重合，只存在上图那样简单的单个环；任何一个点最后只能走到一个环上，无法到达多个环

(2.) 如果每个 环上的点 上都放机器人，不在环上的点不放，根据 (1)，这些机器人全都不会撞在一起，而是会和平的排队转圈圈

(3.) 如果在每个环上都放满机器人，再在环周围延伸出的边上选择一点放机器人，在某一时刻，这个“多余”的机器人一定会走到环上，与环上的一个机器人相撞；也就是说，有一个机器人必须被撤走

所以现在对于每一个环和其延伸出的边，存在两种方法放置机器人：

(1.) 只在环上放机器人，机器人个数是环上点的个数。

(2.) 在环上放 点的个数(-a) 个机器人，在环周围的路径上放 (a) 个机器人，使它们互不相撞。

这两种放法总数是不变的，因此我们得出最多放置机器人的个数就是 在环上的点的个数。只要 (O(n)) 寻找环，标记这些点即可。

在此基础上考虑如何最大化黑点数目。

虽然上面两种放法的总数是一样的，但是无法做到尽可能多选黑点。假设原来是按照放法 (1) 来放置的，现在要在环周围的路径上选择一些点，替换环上的一些点，使黑格数目增加。

显然，对于一次替换，当且仅当路径上新增的点是黑的，环上被替换的点是白的，这次替换才是有意义的。它使黑格数目(+1)。

具体的实现方法是：先找到一个环，设其大小为 (siz)，随便找一个断点把环拉成一条链。枚举环上的每一个点 (j)，搜索所有最后从 (j) 进入环的点（需要注意的是，这个操作仍然是 (O(n)) 的）。如果这个点是黑点，且它与环的距离是 (step)。先让 (step) (mod) (siz)（如果环上的机器人走了一些圈最终归位，跟没走一样），再在链上找到 (j) 往前数 (step) 个是谁，如果是白点，直接替换为黑点。

最后黑色点的最大个数就是：替换完成后，所有在环上的黑点个数。总复杂度 (O(n))。

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <cmath>
 #define id(x,y) ((x - 1) * m + y)
 using namespace std;
 
 const int N = 1000100;
 struct pos { int x, y; } st[N], cy[N];
 int T, n, m, cnt, a1, a2;
 int a[N], dir[N], vis[N], use[N], tag[N];
 int dx[4] = {0, 0, -1, 1}, dy[4] = {-1, 1, 0, 0};
 char ch;
 
 void dfs(int x, int y)
 {
     int xx = x + dx[dir[id(x, y)]], yy = y + dy[dir[id(x, y)]];
     if(vis[id(x, y)])
     {
         st[++cnt].x = x, st[cnt].y = y;
         return ;
     }
     vis[id(x, y)] = 1;
     if(!use[id(xx, yy)]) dfs(xx, yy);
     vis[id(x, y)] = 0, use[id(x, y)] = 1;
 }
 
 void search(int x, int y, int step, int std, int siz)
 {
     vis[id(x, y)] = 1;
     for(int i = 0; i < 4; i++)
     {
         int xx = x + dx[i], yy = y + dy[i];
         if(xx < 1 || yy < 1 || xx > n || yy > m || vis[id(xx, yy)])
             continue;
         int nxtx = xx + dx[dir[id(xx, yy)]];
         int nxty = yy + dy[dir[id(xx, yy)]];
         if(nxtx == x && nxty == y && !tag[id(xx, yy)])
         { 
             if(a[id(xx, yy)] == 0)
             {
                 int new_step = step % siz;
                 int re = std + siz - new_step;
                 if(a[id(cy[re].x, cy[re].y)] == 1)
                     a[id(cy[re].x, cy[re].y)] = 0;
             }
             search(xx, yy, step + 1, std, siz);
         }
     }
 }
 
 int main()
 {
     scanf("%d", &T);
     while(T--)
     {
         scanf("%d%d", &n, &m);
         cnt = a1 = a2 = 0;
         for(int i = 1; i <= n; i++)
             for(int j = 1; j <= m; j++)
             {
                 cin >> ch;
                 a[id(i, j)] = ch - '0';
             }
         for(int i = 1; i <= n; i++)
             for(int j = 1; j <= m; j++)
             {
                 cin >> ch;
                 if(ch == 'L') dir[id(i, j)] = 0;
                 if(ch == 'R') dir[id(i, j)] = 1;
                 if(ch == 'U') dir[id(i, j)] = 2;
                 if(ch == 'D') dir[id(i, j)] = 3;
             }
         for(int i = 1; i <= n; i++)
             for(int j = 1; j <= m; j++)
                 if(!use[id(i, j)]) dfs(i, j);
         for(int i = 1; i <= n; i++)
             for(int j = 1; j <= m; j++)
                 vis[id(i, j)] = 0;
         for(int i = 1; i <= cnt; i++)
         {
             int x = st[i].x, y = st[i].y, tot = 1;
             cy[1].x = x, cy[1].y = y, tag[id(x, y)] = 1;
             while(true)
             {
                 int xx = x + dx[dir[id(x, y)]];
                 int yy = y + dy[dir[id(x, y)]];
                 if(xx == st[i].x && yy == st[i].y) break;
                 tag[id(xx, yy)] = 1;
                 cy[++tot].x = xx, cy[tot].y = yy;
                 x = xx, y = yy;
             }
             for(int j = 1; j <= tot; j++)
                 cy[j + tot].x = cy[j].x, cy[j + tot].y = cy[j].y;
             for(int j = 1; j <= tot; j++)
                 search(cy[j].x, cy[j].y, 1, j, tot);
         }
         for(int i = 1; i <= n; i++)
             for(int j = 1; j <= m; j++)
             {
                 if(tag[id(i, j)] == 1) a1++;
                 if(tag[id(i, j)] == 1 && a[id(i, j)] == 0) a2++;
             }
         for(int i = 1; i <= n; i++)
             for(int j = 1; j <= m; j++)
                 use[id(i, j)] = vis[id(i, j)] = tag[id(i, j)] = 0;
         printf("%d %d
", a1, a2);
     }
     return 0;
 }