油滴扩展

题目链接

Solution

深搜，每次选择一个点放油滴。要求这个油滴的面积，需要知道它的半径。

一个油滴在扩展的过程中碰到第一个油滴、边界就立刻停下，所以我们处理出这个点到每个油滴、边界的距离，在里面取 (min)，就是当前油滴的半径。

一个点到边界的距离比较好求，那么怎么求一个点到其他油滴的距离呢？

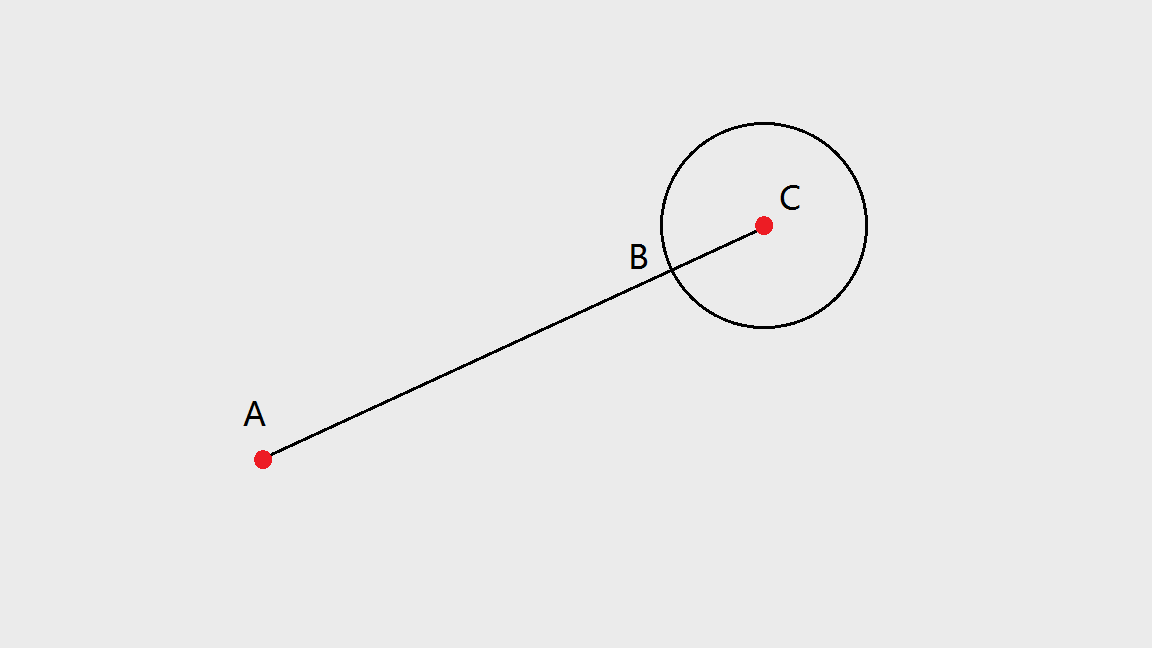
设A点是现在要放油滴的点，C点是另一个油滴的圆心。我们要求的距离是线段AB的长度。(mathrm{AB = AC - BC}). 可以利用两个点的距离公式求出AC的长度，而 (mathrm{BC}) 就是 (mathrm{C}) 点油滴的半径。

一个坐标为 (mathrm{(x1, y1)}) 的到坐标为 (mathrm{(x2, y2)})、半径为 (p_j) 的油滴的距离为：

[sqrt{(x1-x2)^2+(y1-y2)^2}-p_j ]

注意：如果某个油滴在其他油滴的内部，半径为 (0).

Code

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
int n, a1, b1, a2, b2, u, v, w, z, x[104], y[104];
int vis[104];
double pi = 3.14159265358979, p[104], ans = 0x3f3f3f3f;
double dis(int x1, int y1, int x2, int y2) // 两点之间的距离
{
    return (double)(sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2)));
}
void dfs(int tot, double S)
{
    if(ans > S) ans = S;
    if(tot == n) return ; // 油滴都放完了
    for(int i = 1; i <= n; i++)
    {
        if(vis[i] == 0 && x[i] <= u && x[i] >= w && y[i] <= v && y[i] >= z) 
        // 判断在不在方框内部、有没有放过油滴
        {
            vis[i] = 1;
            double minn = min(x[i] - w, min(y[i] - z, min(u - x[i], v - y[i])));
            // 到四个边界的距离
            for(int j = 1; j <= n; j++)
            {
                if(vis[j] == 0 || i == j) continue; // 找到所有放过油滴的点
                minn = min(minn, dis(x[i], y[i], x[j], y[j]) - p[j]); // 更新半径
            }
            if(minn < 0) minn = 0; // 在其他油滴内部
            p[i] = minn; // 记下半径
            dfs(tot + 1, S - pi * minn * minn); // 减去面积
            vis[i] = p[i] = 0; // 回溯
        }
    }
}
int out(double a) // 四舍五入的函数
{
    if((int)(a * 10) % 10 >= 5) return (int)(a + 1);
    return (int)a;
}
int main()
{
    scanf("%d%d%d%d%d", &n, &a1, &b1, &a2, &b2);
    u = max(a1, a2), v = max(b1, b2), w = min(a1, a2), z = min(b1, b2); // 四个边界
    for(int i = 1; i <= n; i++) scanf("%d%d", &x[i], &y[i]);
    dfs(0, abs(a1 - a2) * abs(b1 - b2)); // 方框的面积
    printf("%d", out(ans));
    return 0;
}