Bellman-Ford算法及其队列优化（SPFA）

一、算法概述

        Bellman-Ford算法解决的是一般情况下的单源最短路径问题。所谓单源最短路径问题：给定一个图G=（V,E）,我们希望找到从给定源结点s属于V到每个结点v属于V的最短路径。单源最短路径问题可以用来解决许多其他问题，其中包括下面几个最短路径的变体问题。包括单目的最短路径问题、单结点最短路径问题、所有结点对最短路径问题，这里不详细介绍。回到bellman-Ford,在这里，边的权重可以为负值。给定带权重的有向图G=（V,E）和权重函数W : E-->R,Bellman-Ford算法返回一个布尔值，以表明是否存在一个从源点可以到达的权重为负值的环路。如果存在这样的环路，算法将告诉我们不存在解决方案。如果没有这种环路存在，算法将给出最短路径和它们的权重。边的权值可以为负数、实现简单，缺点是时间复杂度过高，高达O（VE）。但算法可以进行若干种优化，提高了效率。

     自然语言描述

对有向图，用贝尔曼-福特算法求以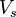为源点的最短路径的过程：

• 建立，表示目前已知源点到各个节点的最短距离，起始值，其余皆为。
• 建立，表示某节点路径上的父节点，起始值皆为NULL。
• 对，比较和,并将小的赋给，如果修改了则（松弛操作）
• 重复以上操作次
• 再重复操作一次，如,则此图存在负权环。

    伪代码表示

BellmanFord(G,s)
 for i = 0 to n-1 do
  dist[i]= ∞
  Pred[i]= 0
 dist[s]=0
 for k = 1 to n-1 do
    foreach ∈ do
      if  do
         
         
foreach ∈ do
      if  do
         return "No Shortest Path"
 return dist[]

二、原理

       为什么说最短路径不存在负环呢？

       如果图G包含从s可以达到的权重为负值的环路，则最短路径权重无定义。从s到该环路上的任意结点的路径都不可能是最短路径，因为我们只要沿着任何“最短”路径再遍历一次权重为负值的环路，则总是可以找到一条权重更小的路径。如果从结点s到结点v的某条路径上存在权重为负值的环路，我们定义s到v的最短路径等于负无穷。

        松弛操作

        它的原理是对图进行V-1次松弛操作，得到所有可能的最短路径。对于一条边（u,v）的松弛过程为：首先测试一下是否可以对源点s到v的最短路径进行改善。测试的方法是，将从结点s到结点u之间的最短路径距离加上结点u与v之间的权重，并与当前的s到v的最短路径估计进行比较，如果前者更小，则对v.d（源点s到v的最短路径） 和v.π（前驱结点）进行更新。

        每次松弛操作实际上是对相邻节点的访问，第次松弛操作保证了所有深度为n的路径最短。由于图的最短路径最长不会经过超过条边，所以可知贝尔曼-福特算法所得为最短路径。

        负边权操作

        与迪科斯彻算法不同的是，迪科斯彻算法的基本操作“拓展”是在深度上寻路，用于有向无环图的最短路径算法对每条边仅松弛一次。Bellman-Ford“松弛”操作则是在广度上寻路，这就确定了贝尔曼-福特算法可以对负边进行操作而不会影响结果。

       负权环判定

        因为负权环可以无限制的降低总花费，所以如果发现第次操作仍可降低花销，就一定存在负权环。

三、队列优化——SPFA

       求单源最短路的SPFA算法的全称是：Shortest Path Faster Algorithm。松弛操作必定只会发生在最短路径前导节点松弛成功过的节点上，用一个队列记录松弛过的节点，可以避免了冗余计算。复杂度可以降低到O(kE)，k是个比较小的系数(并且在绝大多数的图中，k<=2，然而在一些精心构造的图中可能会上升到很高)

       实现方法：建立一个队列，初始时里只有起始点，再建立一个表格记录起始点到所有点的最短路径（该表格的初始值要赋为极大值，该点到他本身的路径赋为0）。然后执行松弛操作，用队列里有的点去刷新起始点到所有点的最短路，如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。重复执行直到队列为空

      判断有无负环：如果某个点进入队列的次数超过N次则存在负环 (存在负环则无最短路径，如果有负环则会无限松弛，而一个带n个点的图至多松弛n-1次。

参考：算法导论、http://zh.wikipedia.org/zh-cn/%E8%B4%9D%E5%B0%94%E6%9B%BC-%E7%A6%8F%E7%89%B9%E7%AE%97%E6%B3%95#.E6.9D.BE.E5.BC.9B

版权声明：本文为博主原创文章，未经博主允许不得转载。