C程序设计实验报告
实验项目:函数的定义和调用
1、编写由三角形三边求面积的函数
2、编写求N阶乘的函数
3、求两个整数的最大公约数
4、打印输出指定图形
姓名:肖伟 实验地点: 514实验室 实验时间:2019年4月30日
一、实验目的与要求
1.编写由三角形三边求面积的函数
- 调用area()函数求三角形的面积
- 在求面积函数运用海伦公式
2、编写求N阶乘的函数
- 定义符号常量
- 使用长整型变量存放累乘积
- 使用全局变量存放累乘积
3、求两个整数的最大公约数
- 调用bcd()函数求两个整数的最大公约数
- 掌握辗转相除法求两个整数的最大公约数
4、打印输出指定图形
- 调用trangle()函数输出三角形
- 在trangle()函数中用for循环的嵌套输出指定的结果
5.模块化程序设计
- 编制一个函数facsum(m),返回给定正整数m的所有因子(包括1但不包括自身)之和
- 编制一个主函数,调用(1)中的函数facsum(),寻找并输出500以内的所有亲密数对
- 输出要有文字说明。在输出每对亲密数时,要求从小到大排列并去掉重复的亲密数对
- 所有函数中的循环均为for循环
二、实验内容
6.4.1.1.编写由三角形三边求面积的函数
1.问题的描述:编写程序,从键盘输入三角形的3条边,调用三角形面积函数求出其面积,并输出结果。
2.流程图:
(1)
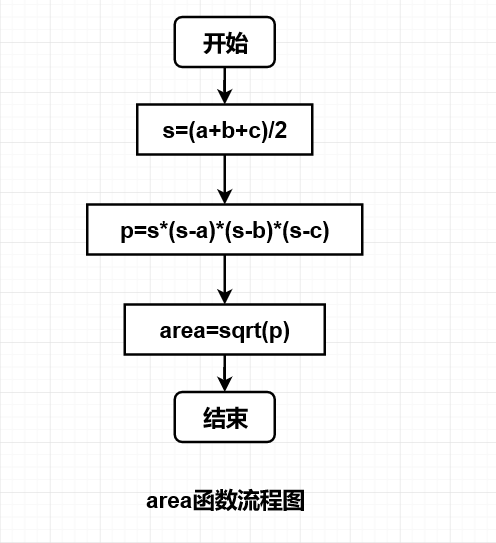
(2)
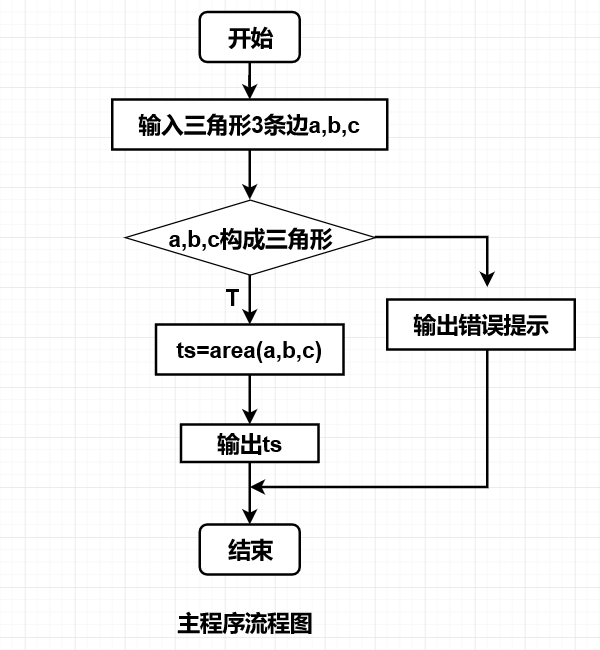
3.实验代码:
#include<math.h> #include<stdio.h> float area(float a,float b,float c) { float s,p,area; s=(a+b+c)/2; p=s*(s-a)*(s-b)*(s-c); area=sqrt(p); return (area); } main() { float x,y,z,ts; scanf("%f,%f,%f",&x,&y,&z); ts=area(x,y,z); if(x+y>z&&x+z>y&&z+y>x) printf("area=%f ",ts); else printf("data error!"); }
4.问题分析: 其实这个题目不难,关键在于我们需要解决“三条边可以构成三角形”需要满足的调件,然后就是要能看懂书上流程图的条件,最后就是我们要会用数学公式来解决问题。
5.运行效果:

6.4.1.2、编写求N阶乘的函数
1.问题的描述:编写函数,求出从主函数传来的数值i阶乘值,然后将其传回主调函数并输出。
2.流程图:

3.实验代码:
#include<stdio.h> #define N 5 long function(int i) { static long f=1; if(i>1) f=i*function(i-1); else return 1; return f; } main() { long product; int i; for(i=1; i<=N;i++) { product=function(i); printf("%d的阶乘是:%ld ",i,product); } }
4.问题分析:我们在这里定义了N=5,说明不能算特别大的数值的阶乘;同时也用到了函数的调用,我们要理解函数的调用才能更好的使程序更加精简。
5.运行效果:
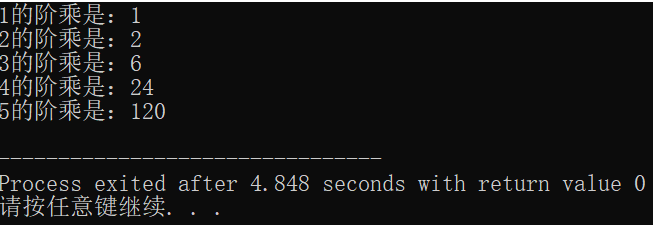
6.4.1.3、求两个整数的最大公约数
1.问题的描述:编写程序,从键盘输入两个整数,调用gcd()函数求他们的最大公约数,并输出结果。
2.流程图:

3.实验代码:
#include<stdio.h> int gcd(int a,int b) { int temp; int remainder; if(a<b) { temp=a; a=b; b=temp; } remainder=a%b; while(remainder!=0) { a=b; b=remainder; remainder=a%b; } return b; } main() { int x,y; int fac; printf("please input two integers:"); scanf("%d,%d",&x,&y); fac=gcd(x,y); printf("The great common divisor is:%d",fac); }
4.问题分析:求两数最大公约数,如果有两个数a,b,如果a>b,a能被b整除,则最大公约数就是b,若a除b的余数为c,则继续用b除c,如此反复操作,直到最后余数为0,则最后一个非0的除数就是a,b的最大公约数,这里要用到辗转相除法(用较小数除较大数,再用出现的余数(第一余数)去除除数,再用出现的余数(第二余数)去除第一余数,如此反复,直到最后余数是0为止。
一开始我的代码少了
remainder=a%b这个代码,所以运行不出来,后面加了才运行出来了。
5.运行效果:
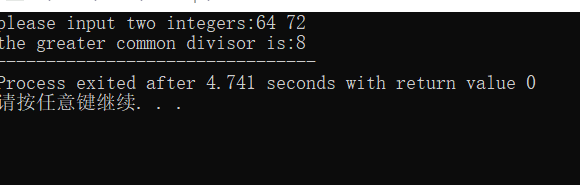
6.4.1.4、打印输出指定图形
1.问题的描述:输入整数n,输出高度为n的等边三角形,当n的值为5,等边三角形为:
*
***
*****
*******
**********
2.流程图:
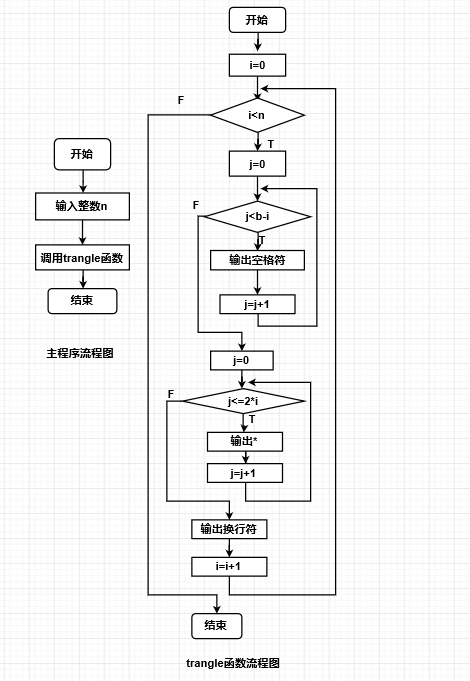
3.实验代码:
#include<stdio.h> trangle(int n) { int i,j; for (i=0;i<n;i++) { for (j=0;j<n-i;j++) { printf(" "); } for (j=0;j<=2*i;j++) { printf("*"); } printf(" "); } } main() { int n; printf("请输入一个整数:"); scanf("%d",&n); printf(" "); trangle(n); }
4.问题分析:我们发现等边三角形的组成规律,每一行星号前的空格都比上一行的少一个,每一行的星号个数也是有规律的,可以用2i-1来表示n表示行,i表示第几行,而j表示*,我们可以发现图形总共有5行,第一行前面是4个空格,第二行3个空格,第三行2个空格······以此类推可以知道j=n-i,然后j<=2*i,根据这个规律编写一个trangle()函数,然后在调用该函数就可以打印出高度为5的等边三角形。
5.运行效果:
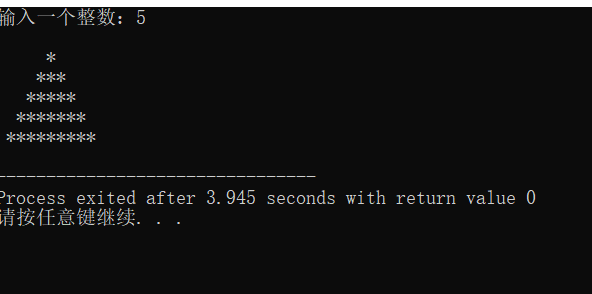
6.4..2.1模块化程序设计
1,问题描述:若正整数A的所有因子(包括1但不包括自身,下同)之和为B,而B的因子之和为A,则称A和B为一对亲密数。例如,6的因子之和为1+2+3=6,因此6与6为一对亲密数(即6自身构成一对亲密数);又如,220的因子之和为1+2+4+5+10+11+20+22+44+55+110=284,而284的因子之和为1+2+4+71+142=220,因此,220与284为一对亲密数。
求500以内的所有的亲密数对。
2,流程图:

3.实验代码:
#include<stdio.h> int facsum(int m) { int sum=1,f=2; while(f<=m/2) { if(m%f==0) sum=sum+f; f++; } return sum; } main() { int m=3,n,k; while(m<=500) { n=facsum(m); k=facsum(n); if(m==k&&m<=n) printf("%d %d ",m,n); m++; } }
4.问题分析:首先我们要理解一对亲密数到底是什么意思,然后进行分析。然后在facsum(m)模板中,求出m的所有因子,并将它们的和作为返回值,看返回后得出的第二个因子之和是否与本事的因子之和相等,如果相等则输出两个数,这里又要用到循环语句,我们须当心。
5.运行效果:

三、实验小结:
这节课我主要是对调用函数有了更深的了解,在调用函数的同时,我们都要先设计一个函数,但在后面调用函数的时候,我们需对其名称有一定的了解,这样就不会出现不必要的错误了在第二个程序中product=function(i);而第四个程序中直接trangle (n);前面并没有**=trangle(n);所以这是我们需要注意的。还有就是我们也要对以前学过的方法有一定的掌握,比如在第二个程序中有a与b交换值的问题,我们就要想起以前老师讲的用第三个杯子的问题。