数值计算可以分为两类:矩阵运算和矩阵元素运算
3.1 矩阵函数和特殊矩阵
矩阵代数的处理数组大部分以一维数组(向量)和二维数组(矩阵)为主。
常见的矩阵处理函数如下:
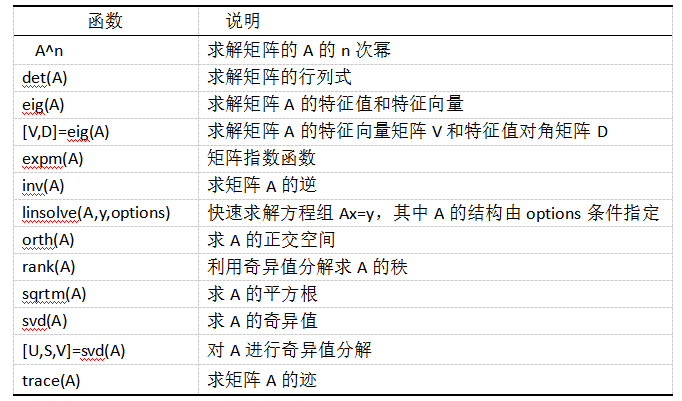
特殊矩阵:
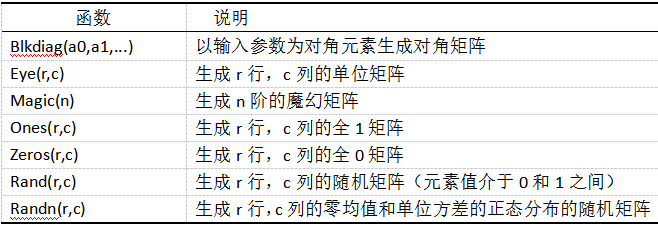
稀疏矩阵:
稀疏矩阵的创建通常可以通过使用sparse和spdiags函数来进行:
- sparse(i,j,s,m,n,nz_max)使用[i,j,s]来创建m*n维稀疏矩阵s,其中s为所有非零元素构成的向量,i,j分别为非零元素的行下标和列下标。
- spdiags(B,d,m,n)可以抽取、创建或替代对角稀疏矩阵,其中m和n分别为矩阵的行和列的维数,d表示长度为p的整数向量,B为满矩阵。
- 稀疏矩阵和满矩阵之间可以通过sparse和full函数进行转换。
- spy(A)画出A矩阵
3-2 矩阵分析
- 范数分析:norm()函数可以用来求解向量和矩阵的范数,
如 n2=norm(x),ninf=norm(x,inf),nneg_inf=norm(x,-inf)分别求解二范数,无穷范数和负无穷范数
求解大型矩阵的范数和稀疏矩阵时,可以考虑采用normest来求解。
- 条件数分析:矩阵的条件数总是大于1,正交矩阵的条件数等于1,奇异矩阵的条件数为无穷大,
病态矩阵的条件数是比较大的数据。 矩阵的条件数可以通过函数cond()求解。
3.3 线性方程组
下面介绍三种方程组:恰定方程组、超定方程组、欠定方程组。
- 恰定方程组:方程组的个数和未知数的个数相等,分为奇异和非奇异两种。
%求解非奇异恰定方程组的解
>> A=[1 2 3;4 5 6;7 8 0];
>> y=[366;804;351]
%方法一:判断A的条件数、秩以及增广矩阵[A y]的秩
>> rank(A)
>>rank([A y])
>> cond(A)
>> x_1=inv(A)*y
>> %方法2 通过矩阵左除来求解线性方程组的解,LU分解,速度快
>> x_2=A\y
%求解奇异恰定方程组的解
>> A=[1 3 7;-1 4 4;1 10 18];
>> y=[6;4;15];
>> %方法1:通过矩阵左除来求解线性方程组的解
>> x_1=A\y
>> %方法2 判断A的条件数、A的秩以及增广矩阵[A y]的秩
>> det_A=det(A)
>> rank_A=rank(A)
>> rank_Ay=rank([A y])
>> cond_A=cond(A)
>> x_2=pinv(A)*y;
>> disp(x_2)
- 欠定方程组:方程组的个数小于未知数的个数,存在无数个解。最小范数解,略。
方法1:左除法:x_1=A\y
方法2:伪逆矩阵法(范数最小)
x_2=pinv(A)*y
- 超定方程组:方程组的个数大于未知数的个数,存在无数个解。最小二乘解,略。
3.4 矩阵分解
主要包括Cholesky 分解、LU分解和QR分解
3.5 特征值分析(略)