说到递归算法,应该无人不知,那怎么算递归算法的时间复杂度,我想应该不一定每个人都知道了,所以下面来学习学习。
对于递归算法举例,最经典的就是斐波那契数列了,而它的定义也贴一下:

下面用代码来实现它:
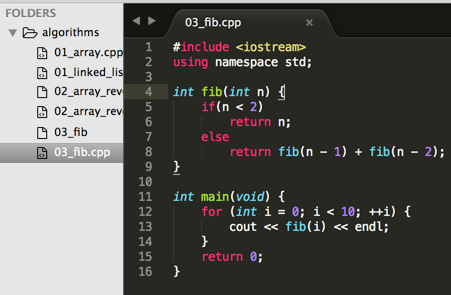
不多解释,因为比较容易,下面来看下输出结果:

那该递归算法的时间复杂度是多少呢?应该时间耗得不多吧,看下面这个实验,把运行次数由10改到50,直观来感受一下:
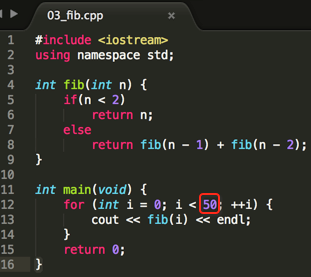
运行结果:

仔细的观察一下输了结果,是不是从快到慢,而且后面慢得已经是需要等半分钟才能算出一个数了,可见递归的时间损耗是相当吓人的~
下面具体来算一下它的时间复杂度:

而重点是分析下面这个条件分支:

可以得到t(n) = t(n-1) + t(n-2) + O(1);其中O(1)表示中间有一个加法运算,这是常量级别的。
那如何换算成大O表达示呢?这里采用自然归纳法【当然还有其它换算方法,反正我也不知道~】,看下面:
当n=0或1时它的时间复杂度是O(1),而它是<=O(2 ^ n)的,这是假设,怎么论证呢:当n=0时数=2^0,而当n=1时数<2^1;
这时可以假设斐波那契数列递归算法的时间复杂度就是<=O(2 ^ n)
进一步假设:时间复杂度是O(2 ^n)在t(n-1)上也成立,那么基于t(n) = t(n-1) + t(n-2) + O(1);可以换算为:
t(n) = O(2^(n-1)) + O(2^(n-2)) + O(1);
而O(2^(n-2))是O(2^(n-1))时间的一半,所以O(2^(n-2))=0.5 * O(2^(n-1)),于是乎:
t(n) = 1.5 * O(2^(n-1)) + O(1);
而1.5 * O(2^(n-1)) + O(1) <= 2 * O(2^(n-1)) + O(1) <= O(2 ^ (1+n-1)) + 0(2 ^ 0) <= O(2 ^n)
也就是t(n) <= O(2 ^n)
所以斐波那契数列递归算法的时间复杂度就是<=O(2 ^ n),所以这就可以看到为啥上面的i增大到50时运行速度非常非常慢了,因为递归实现时间复杂度是指数级别增长的,所以进一步论证大O表示法确实比较清晰的很衡量一个算法设计的好坏了。