状态机dp学习笔记_AcWing

1.AcWing 1057 股票交易4

#include<bits/stdc++.h>
#pragma GCC optimize(2)
#define ll long long
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define per(i,n,a) for(int i=n;i>=a;i--)
#define endl '
'
#define eps 0.000000001
#define pb push_back
#define mem(a,b) memset(a,b,sizeof(a))
#define IO ios::sync_with_stdio(false);cin.tie(0);
using namespace std;
const int INF=0x3f3f3f3f;
const ll inf=0x3f3f3f3f3f3f3f3f;
const int mod=1e9+7;
const int maxn=110+5;
int a[maxn],dp[maxn][maxn][2];
int main(){
    int n,m;cin>>n>>m;
    rep(i,1,n) cin>>a[i];
    mem(dp,-INF);
    rep(i,0,n) dp[i][0][0]=0; 
    rep(i,1,n){
        rep(j,1,m){
            dp[i][j][0]=max(dp[i-1][j][0],dp[i-1][j][1]+a[i]);
            dp[i][j][1]=max(dp[i-1][j][1],dp[i-1][j-1][0]-a[i]);
        }
    }
    int ans=0;
    rep(i,1,m){
        ans=max(ans,dp[n][i][0]);
    }
    cout<<ans<<endl;
}

2.AcWing 1058股票交易5

#include<bits/stdc++.h>
#pragma GCC optimize(2)
#define ll long long
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define per(i,n,a) for(int i=n;i>=a;i--)
#define endl '
'
#define eps 0.000000001
#define pb push_back
#define mem(a,b) memset(a,b,sizeof(a))
#define IO ios::sync_with_stdio(false);cin.tie(0);
using namespace std;
const int INF=0x3f3f3f3f;
const ll inf=0x3f3f3f3f3f3f3f3f;
const int mod=1e9+7;
const int maxn=1e5+5;
int w[maxn],dp[maxn][3];
int main(){
    int n;scanf("%d",&n);
    rep(i,1,n) scanf("%d",&w[i]);
    rep(i,0,n+2) dp[i][0]=dp[i][1]=-INF;
    rep(i,1,n){
        dp[i][2]=max(dp[i-1][1],dp[i-1][2]);
        dp[i][1]=dp[i-1][0]+w[i];
        dp[i][0]=max(dp[i-1][0],dp[i-1][2]-w[i]);
    }     
    printf("%d
",max(dp[n][1],dp[n][2]));
}

 3.AcWing 1052涉及密码(KMP+状态机DP)

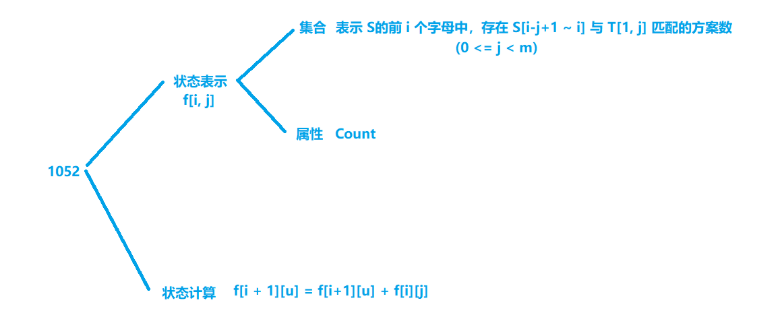
 我认为这是一个暴力匹配的过程，但不失状态机模型转移的一般性。通俗一点来说，dp[i][j]表示我处理到S串的第i个位置和T串的第j个位置，现在要处理第S[i+1]个位置，我们知道S[i+1]存在‘a’~'z'共26种可能，所以我们需要kmp一步一步往前挪，直到匹配成功，这时候我们用u代替j，因为S[i+1]或许并不一定与原先的p[j+1]相等，此时就需要转移了，根据kmp的next数组，我们知道既然目前已经匹配，那么j往前跳也肯定在后缀是匹配的，直到跳到0为止（我写的代码是-1为止，next初始定义不同）。我们用u起先代替j来跳就可，最后dp[i+1][u]=(dp[i+1][u]+dp[i][j])，因为i+1，u可以由i，j转移得到

#include<bits/stdc++.h>
#pragma GCC optimize(2)
#define ll long long
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define per(i,n,a) for(int i=n;i>=a;i--)
#define endl '
'
#define eps 0.000000001
#define pb push_back
#define mem(a,b) memset(a,b,sizeof(a))
#define IO ios::sync_with_stdio(false);cin.tie(0);
using namespace std;
const int INF=0x3f3f3f3f;
const ll inf=0x3f3f3f3f3f3f3f3f;
const int mod=1e9+7;
const int maxn=1e5+5;
int n,net[maxn];char p[maxn];
void getnext(char *p){
    int lenp=strlen(p);
    net[0]=-1;
    int k=-1;
    int j=0;
    while(j<lenp){
        if(k==-1||p[j]==p[k]){
            j++;k++;
            net[j]=k;
        }
        else
            k=net[k];
    }
}
int dp[55][55];
int main(){
    cin>>n;scanf("%s",p);
    getnext(p);
    int m=strlen(p);
    dp[0][0]=1;
    for(int i=0;i<n;i++){
        for(int j=0;j<m&&i-j+1>0;j++){
            for(char k='a';k<='z';k++){
                int u=j;
                while(u!=-1&&k!=p[u]) u=net[u];
                ++u;
                if(u<m){
                    dp[i+1][u]=(dp[i+1][u]+dp[i][j])%mod;
                }
            }
        }
    }
    int res=0;
    for(int i=0;i<m;i++){
        res=(res+dp[n][i])%mod;
    }
    cout<<res<<endl;
}

 AcWing1053(POJ3691).修复DNA(AC自动机+状态dp)

#include<bits/stdc++.h>
#pragma GCC optimize(2)
#define ll long long
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define per(i,n,a) for(int i=n;i>=a;i--)
#define endl '
'
#define eps 0.000000001
#define pb push_back
#define mem(a,b) memset(a,b,sizeof(a))
#define IO ios::sync_with_stdio(false);cin.tie(0);
using namespace std;
const int INF=0x3f3f3f3f;
const ll inf=0x3f3f3f3f3f3f3f3f;
const int mod=1e9+7;
int n;
int getid(char c){
    if(c == 'A') return 0;
    if(c == 'C') return 1;
    if(c == 'G') return 2;
    if(c == 'T') return 3;
}
class ac_auto{
    public:
        const static int maxn=5e4+100;
        int tot,root;
        int tree[maxn][5]; 
        bool End[maxn];
        int fail[maxn];int ans[1005];
        int newnode(){
            for(int i=0;i<4;i++){
                tree[tot][i]=0;
            }
            End[tot]=0;
            return tot++;
        }
        void init(){
            mem(ans,0);tot=0;
            root=newnode();
        }                
        void insert_(string s){
            int now = root;
            for(int i=0;i<s.length();i++){
                int id=getid(s[i]);
                if(!tree[now][id]){
                    tree[now][id]=newnode();
                }
                now=tree[now][id];
            }
            End[now]=true;
        }
        
        void getFail(){
            queue <int>q;
            for(int i=0;i<4;i++){
                if(tree[0][i]){
                    fail[tree[0][i]] = 0;
                    q.push(tree[0][i]);
                }
            }
            while(!q.empty()){
                int now = q.front();
                q.pop();
                for(int i=0;i<4;i++){
                    if(tree[now][i]){
                        fail[tree[now][i]] = tree[fail[now]][i];
                        End[tree[now][i]]|=End[tree[fail[now]][i]];
                        q.push(tree[now][i]);
                    }
                    else
                        tree[now][i] = tree[fail[now]][i];
                }
            }
        }    
        
}acam;
int dp[1010][1010];
int main(){
    int T=1;
    while(cin>>n&&n){
        acam.init();
        rep(i,1,n){
            string s;cin>>s;
            acam.insert_(s);
        }
        acam.getFail();
        string a;
        cin>>a;
        int len=a.length();
        a=" "+a;
        mem(dp,INF);
        dp[0][0]=0;
        for(int i=0;i<len;i++){
            for(int j=0;j<acam.tot;j++){
                for(int k=0;k<4;k++){
                    int t=getid(a[i+1])!=k;
                    int p=acam.tree[j][k];
                    if(!acam.End[p]) dp[i+1][p]=min(dp[i+1][p],dp[i][j]+t);
                }
            }
        }        
        int res=INF;
        for(int i=0;i<acam.tot;i++) res=min(res,dp[len][i]);
        if(res==INF) res=-1;
        printf("Case %d: %d
",T++,res);
    }
}