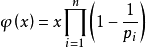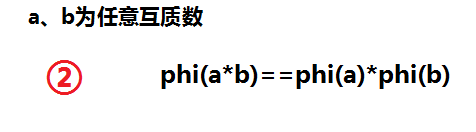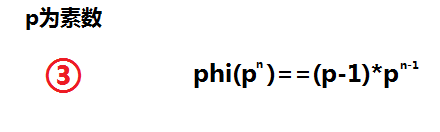写在前面:
记录了个人的学习过程,同时方便复习
整理自网络
非原创部分会标明出处
目录
|
|
在数论中,欧拉定理(也称费马-欧拉定理或欧拉函数定理)是一个关于同余的性质 欧拉定理表明,若n,a为正整数,且n,a互质,则: aφ(n) ≡ 1 (MOD n) ——bia度百科 |
|
欧拉函数 在数论,对正整数n>1,欧拉函数是小于n的正整数中与n互质的数的数目(φ(1)=1)
(其中p1, p2……pn为x的所有质因数,x是不为0的整数) ——bia度百科 |
|
欧拉函数五个性质
|
(某一种证法,需要了解一下[◹]同余定理里面的同余类,剩余类,简化剩余类)
将1~n中与n互质的数按顺序排布:x1,x2……xφ(n),显然,共有φ(n)个数
我们考虑这么一些数:
m1 == a*x1
m2 == a*x2
m3 == a*x3
……
mφ(n) == a*xφ(n)
①这些数中的任意两个都不模n同余,因为如果有mS ≡ mR (mod n) (这里假定mS更大一些),就有:
mS-mR == a(xS-xR) == qn
即n能整除a(xS-xR)
但是a与n互质,a与n的最大公因子是1,而xS-xR<n,因而左式不可能被n整除
也就是说这些数中的任意两个都不模n同余,φ(n)个数有φ(n)种余数
②这些数除n的余数都与n互质,因为如果余数与n有公因子r,那么
a*xi == pn+qr == r(……) a*xi与n不互质
而这是不可能的
那么这些数除n的余数,都在x1,x2,x3……xφ(n)中,因为这是1~n中与n互质的所有数,而余数又小于n
由①和②可知,数m1,m2,m3……mφ(n)(如果将其次序重新排列)必须相应地同余于x1,x2,x3……xφ(n)
故得出:m1*m2*m3……*mφ(n) ≡ x1*x2*x3……*xφ(n) (mod n)
此处证明可见[◹]线性同余方程组中的可乘性
或者说aφ(n)*(x1*x2*x3……*xφ(n)) ≡ x1*x2*x3……*xφ(n) (mod n)
或者为了方便:K{aφ(n)-1} ≡ 0 ( mod n ) 这里K=x1*x2*x3……*xφ(n)
可知K{aφ(n)-1}被n整除,但K中的因子x1,x2……都与n互质,所以K与n互质
那么aφ(n)-1必须能被n整除,即aφ(n)-1 ≡ 0 (mod n),即aφ(n) ≡ 1 (mod n),得证
——bia度百科
-
费马小定理
ap-1 ≡ 1 (MOD p) (p为素数,ap互素)
证明:
据欧拉定理,有aφ(n) ≡ 1 (MOD n)
当n为素数时,有φ(n) == n-1
即an-1 ≡ 1 (MOD n) (n为素数)
费马小定理常应用于有关素数的问题
-
简化幂的模运算
如计算7222的个位数,实际是求7222被10除的余数
7和10互素,且φ(10)=4
由欧拉定理知74 Ξ 1 (MOD 10)
所以7222 == (74)55 * (72) Ξ 155 * 72 Ξ 49 Ξ 9 (mod 10)
-
群论
欧拉函数实际上是模n的同余类所构成的乘法群(即环 Z/nZ的所有单位元组成的乘法群)的阶
毕竟aφ(n) ≡ 1 (MOD n),则aφ(n)是mod n群里面的单位元
欧拉定理也指出了,当a与n互素时,a的指数的一个周期长度为φ(n),但不一定是最小正周期