拟阵

写在前面

　　对于拟阵的学习，便于复习

　　所有资料写得都很像，比如百度百科和维基百科写的差不多就没什么区别

　　摘录自网络，标明出处

定义

　　在组合数学中，拟阵是一个对向量空间中线性独立概念的概括与归纳的数学结构。拟阵有许多等价的定义方式，最常见的定义方式是用独立集，基，圈，闭集合，闭平面，闭包算子或秩函数

　　拟阵理论广泛地借用了线性代数和图理论的术语，因为它是这些领域的重点概念的抽象

　　拟阵在几何，拓扑学，组合优化，网络理论和编码理论上都有很多应用。它抽象了很多图的性质．为组合优化问题和设计多项式算法提供了强有力的工具

——bia度百科

子集系统是一个二元组M=(S,L)，它满足下面三个条件：

(1)S是一个有限集

(2)L是由S的一些子集组成的有限非空集

(3)遗传性和交换性

——信息学奥赛之数学一本通

　　遗传性：对于任意的B⊆L，任意的A⊆B，有A⊆L(可知空集必须是L的元素)

　　交换性：对任意的A⊆L，B⊆L，|A|＜|B|，存在一个x∈B-A，使得A∪{x}⊆L

　　不太好理解，画了两张Venn图：

　　遗传性：

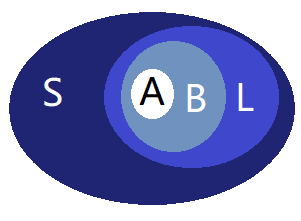
　　交换性：

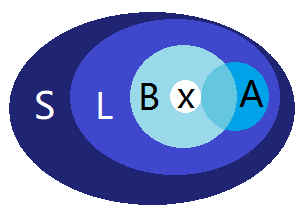
一个拟阵M是一个有序对M=(S,L)，其中S是一个有限非空集合，L⊆S，有以下三大公理：

(1)∅∈L，即L不为空，称为拟阵的独立集公理

(2)M具有可遗传性

(3)M具有交换性，称为独立扩充公理

常见的拟阵问题：向量子集优化问题，背包问题，Kruskal，贪心等

——程序设计中的组合数学

　　Venn图同上

　　In combinatorics, a branch of mathematics, a matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces. There are many equivalent ways to define a matroid, the most significant being in terms of independent sets, bases, circuits, closed sets or flats, closure operators, and rank functions

　　Matroid theory borrows extensively from the terminology of linear algebra and graph theory, largely because it is the abstraction of various notions of central importance in these fields. Matroids have found applications in geometry, topology, combinatorial optimization, network theory and coding theory

　　There are many equivalent (cryptomorphic) ways to define a (finite) matroid

——Wikipedia

译：

　　在组合数学中，拟阵是一种抽象和概括向量空间中线性独立概念的结构。定义拟阵的方法有很多，其中最重要的是独立集、基、电路、闭集或平面、闭算子和秩函数

　　拟阵理论广泛借用线性代数和图论的术语，主要是因为它是这些领域中各种重要概念的抽象。拟阵在几何学、拓扑学、组合优化、网络理论和编码理论等领域有着广泛的应用

　　定义（有限）拟阵有许多等价（隐式）方法

• 独立集

　　就独立来说，一个有限的拟阵 M 是一个二元组(E,L)其中E是一个有限集(称之为基础集) ，
　　L是一个由E的子集构成的集族(称之为独立集)它需要满足下面的条件：

　　　　1. 空集是独立的，也就是说，∅∈L

　　　　　　换个说法就是，至少有一个E的子集是独立的，即L≠∅

　　　　2. 每个独立集的子集是独立的，即： 对于每个子集A'⊆A⊆E，如果A⊆L，则A‘⊆L，有时我们称之为遗传特性

　　　　3. 如果A和B是L的两个独立集，A比B有更多的元素，则在A中存在一个元素，当其加入B时得到一个比B更大独立集

　　　　　　有时我们称之为扩充特性或者叫独立集交换特性

　　　　　　2，3两个特性定义了一个公认的组合结构，叫做独立系统

 ——bia度百科

• 基，圈

　　对于一个基础集的子集，如果它不是独立的，那么我们称它为不独立集

　　对于拟阵M中的一个独立集A，如果加入基础集E中任何一个元素后，A都变为不独立集，那么我们称A是最大独立集，也叫做拟阵的基

　　对于拟阵M中的一个不独立集B，如果它的任何一个真子集都是独立的，那么我们称B是最小不独立集，也叫做拟阵的圈

　　之所以这里出现了圈，是因为拟阵中的圈正好与图论中图的环相对应

　　独立集，基或圈都能完整地描述拟阵：一个集合是独立的当且仅当它不是不独立集，当且仅当它是基的一个子集，当且仅当它不包含任何圈

　　不独立集的集合，基的集合，圈的集合都拥有能作为拟阵公理的性质

　　例如，我们可以用元组(E，β)定义拟阵M，其中E是一个有限集，β是E的子集的集合，我们称之为“基集”，有以下性质：

　　　　1.β不是空集

　　　　2. 如果A和B是β中不同的元素，并且 ，那么存在一个元素，使得

（这里的斜杠表示差集，该性质称为基交换性质）

　　根据基交换性质我们可以得出结论，β 中没有一个元素是其它元素的真子集

 ——bia度百科

• 秩函数

　　两个拟阵的基具有相同数量的元素，它是拟阵理论的一个基础结论，这与线性代数中的基公理类似，基的元素的个数称为似阵的秩

　　如果M是一个E上的拟阵，并且A是E的一个子集，那么A上的拟阵可以通过把一个A的子集当作是独立集来定义当且仅当这个子集在M中是独立集

　　这个性质使得我们可以讨论子拟阵和E中任何子集的秩

　　子集A的秩通过秩函数  来定义，它有以下几种性质：

　　　　1. 秩函数的值总是非负的

　　　　2. 对于任意E的子集A，有

 　　　　3. 对于E的任意两个子集A 和B ，有，这意味着秩函数是一个子模函数

 　　　　4. 对于任意集合A和元素x，有

　　这些属性可以被用来替换有限拟阵的定义：如果(E,r)满足这些属性，那么E上的拟阵独立集可以定义为E的子集A，且A满足

　　子集A的元素个与其秩的差  叫作A的零化度或补秩。它是从A中移除元素使得A成为独立集的最小移除数量

　　E在拟阵M上的零化度叫做M的零化度或M的补秩

 ——bia度百科

• 闭包算子

　　设M是有限集E上的一个拟阵，其秩函数有上述定义。E的子集A的闭包cl(A)的定义如下：

　　闭包算子  拥有如下性质，其中 表示幂集

　　　　1. 对于E的所有子集X，有

　　　　2. 对于E的所有子集X，有

　　　　3.对于E的所有子集X和Y，如果，那么

　　　　4. 对于E的所有元素a和b，所有子集Y，如果那么

　　前三个性质是闭包算子的定义，第四个性质叫做Mac Lane–Steinitz交换性质

　　这些性质也可以当作是拟阵的另一个定义，每个遵守这些性质的决定一个拟阵

 ——bia度百科

• 平面

　　我们称闭包等于自身的集合是封闭的，这样的集合也叫做拟阵的平面或子空间

　　如果一个集合的秩达到了最大，那么这个集合是封闭的，也就是说往该集合中加入任何元素都不会使它的秩变大

　　拟阵上的封闭的集合有以下性质：

　　　　1.E是封闭的

　　　　2. 如果S和T都是平面，那么也是一个平面

　　　　3. 如果S是一个平面，那么平面T覆盖S（意味着T真包含S但S和T间不存在平面U），划分了ES中的元素

 ——bia度百科

• 超平面

　　在一个秩为r的拟阵中，秩为r-1的平面称为超平面，它是平面的最大真子集，也就是说超平面的唯一父集是E，它拥有拟阵的所有元素

　　超平面也叫做补原子，补原子是一个E的一个不能生成M子集，但往它加入任何元素都可以产生生成集

　　拟阵的超平面系拥有以下属性，它也被认为是拟阵的另一个公理

　　　　1.超平面系中不存在不同的使得的X和Y，也就是说超平面是一个Sperner系

 　　　　2.对于每个和不同的，如果，那么存在，并且有 

 ——bia度百科