三角函数

写在前面：

　　高考复习笔记

http://azureprane.deviantart.com/art/Where-Fillies-Fear-to-Tread-Cover-520079756?ga_submit_new=10%253A1426418329

目录

---

• 定义

• 历史

• 类型

• 定理

• 公式

定义

 　　三角函数是基本初等函数之一，是以角度（数学上最常用弧度制）为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。

　　常见的三角函数包括正弦函数、余弦函数和正切函数。在航海学、测绘学、工程学等其他学科中，还会用到如余切函数、正割函数、余割函数、正矢函数、余矢函数、半正矢函数、半余矢函数等其他的三角函数。

　　不同的三角函数之间的关系可以通过几何直观或者计算得出，称为三角恒等式。

——bia度百科

历史

　　三角学的起源与发展早期的三角学是天文学的一部分，后来研究范围逐渐扩大，变成以 三角函数为主要对象的学科。

　　现在,三角学的研究范围已不仅限于三 角形，且为数理分析之基础,研究实用科学所必需之工具。

　　中国的发展我国古代没有出现角的函数概念，只用勾股定理解决了一些三角学范围内的实际问题。

——豆丁网

　　想要精确获知每颗星的经纬度，涉及到非常复杂的坐标转换运算，需要解三角比率，从现代数学来看，就是要解三角函数。

　　Hipparcos因此创立了三角学。他把每一个三角形（无论是平面三角形或者球面三角形）都当做圆内的一个内接三角形，这样三角形的每一个边都变成了一个弦，为了计算三角形的各个部分，我们必须把弦长作为圆心角的函数，而这就成了三角学在接下来几个世纪中的主要任务。

　　据说Hipparcos一共写了12本关于弦长计算的书，但是后来都失传了。而Ptolemy《至大论》中的正弦函数表和弦长的计算方法或许直接来自Hipparcos的著作。毕竟早在公元前二世纪时，Hipparcos就将自己所推知的正弦函数大量应用在实际计算中了。

——http://blog.sina.com.cn/s/blog_6c2b4fe60102dvy4.html

类型

　　八角图：

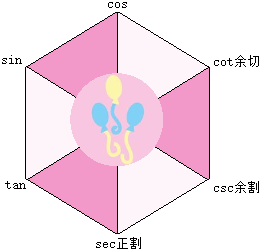
　　　　①平方关系

　　　　　　三个阴影三角形：上面两个角的平方和等于下面角的平方

　　　　　　sin²A+cos²A=1

　　　　　　tan²A+1=sec²A

　　　　　　cot²A+1=csc²A

　　　　②倒数关系

　　　　　　对角线上两个端点成倒数

　　　　　　sinA*cscA=1

　　　　　　cosA*secA=1

　　　　　　tanA*cotA=1

　　　　③商数关系

　　　　　　六边形的相邻三个顶点：中间的数等于两侧的乘积

　　　　　　sinA=cosA*tanA 

　　　　　　tanA=sina*cscA

　　　　　　secA=tanA*cscA

　　　　　　cscA=secA*cotA

　　　　　　cotA=cscA*cosA

　　　　　　cosA=cotA*sinA

定理

　　正弦定理

　　　　对于边长为a、b、c而相应角为A、B、C的三角形，有：（R是三角形的外接圆半径）

　　余弦定理

　　　　对于边长为a、b、c而相应角为A、B、C的三角形，有：

　　　　　　a² = b² + c² - 2bc·cosA

　　　　　　b² = a² + c² - 2ac·cosB

　　　　　　c² = a² + b² - 2ab·cosC

　　　　也可表示为：

　　　　　　

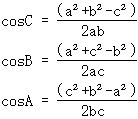
　　正切定理

　　　　对于边长为a、b、c而相应角为A、B、C的三角形，有：

　　　　　　

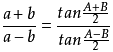
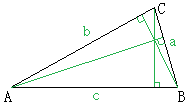
　　射影定理（欧几里德定理）

　　　　对于边长为a、b、c而相应角为A、B、C的三角形，有：

　　　　　　a = bcosC + ccosB

　　　　　　b = ccosA + acosC

　　　　　　c = acosB + bcosA

公式

 　　和差角

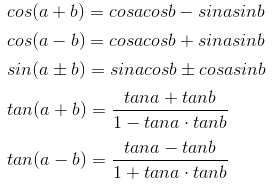
　　积化和差

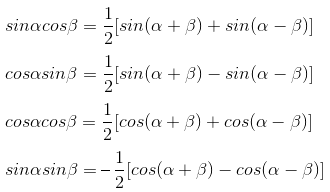
　　和差化积

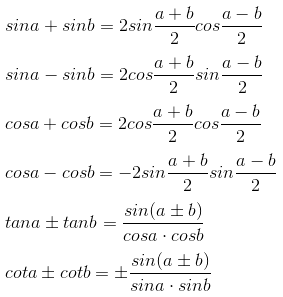
　　二倍角（/半角/升幂降角）

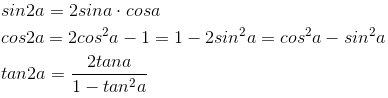
　　降幂升角