zoukankan html css js c++ java

Codeforces 989 P循环节01构造 ABCD连通块构造思维对云遮月参考系坐标轴转换

直接判存不存在连续的三个包含A,B,C就行

/*Huyyt*/
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int dir[8][2] = {{0, 1}, {1, 0}, {0, -1}, { -1, 0}, {1, 1}, {1, -1}, { -1, -1}, { -1, 1}};
const int mod = 1e9 + 7, gakki = 5 + 2 + 1 + 19880611 + 1e9;
const int MAXN = 1e5 + 5, MAXM = 1e5 + 5, N = 2e5 + 5;
const int MAXQ = 100010;
int sum[105];
char f[105];
int main()
{
        ios_base::sync_with_stdio(0);
        cin.tie(0);

        string a;
        cin >> a;
        int len=a.size();
        for (int i = 0; i < a.size(); i++)
        {
                int l = max(i - 1, 0);
                int r = min(len - 1, i + 1);
                if (a[i] == 'A')
                {
                        for (int j = l; j <= r; j++)
                        {
                                sum[j] += 1;
                        }
                }
                else if (a[i] == 'B')
                {
                        for (int j = l; j <= r; j++)
                        {
                                sum[j] += 10;
                        }
                }
                else if (a[i] == 'C')
                {
                        for (int j = l; j <= r; j++)
                        {
                                sum[j] += 100;
                        }
                }
        }
        for (int i = 0; i < a.size(); i++)
        {
                if (sum[i] == 111)
                {
                        cout << "Yes" << endl;
                        return 0;
                }
        }
        cout << "No" << endl;
        return 0;
}

View Code

下列情况有答案

1.f[i]!=f[i-p]

2.f[i]=f[i-p]='.'

3.f[i]!='.'&&f[i-p]='.'或者f[i]='.'&&f[i-p]!='.'

不是这几种情况直接输出NO即可是的话先构造出一处然后剩下的随便赋值了

/*Huyyt*/
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int dir[8][2] = {{0, 1}, {1, 0}, {0, -1}, { -1, 0}, {1, 1}, {1, -1}, { -1, -1}, { -1, 1}};
const int mod = 1e9 + 7, gakki = 5 + 2 + 1 + 19880611 + 1e9;
const int MAXN = 1e5 + 5, MAXM = 1e5 + 5, N = 2e5 + 5;
const int MAXQ = 100010;
int sum[105];
char f[2005];
int main()
{
        ios_base::sync_with_stdio(0);
        cin.tie(0);


        int flag = 0;
        int n, p;
        scanf("%d %d", &n, &p);
        scanf("%s", f + 1);
        for (int i = p + 1; i <= n; i++)
        {
                if (f[i] == '.')
                {
                        if (f[i - p] != '.')
                        {
                                if (f[i - p] == '1')
                                {
                                        f[i] = '0';
                                }
                                else
                                {
                                        f[i] = '1';
                                }
                                flag = 1;
                        }
                        else
                        {
                                f[i] = '0';
                                f[i - p] = '1';
                                flag = 1;
                        }
                }
                else
                {
                        if (f[i - p] == '.')
                        {
                                if (f[i] == '1')
                                {
                                        f[i - p] = '0';
                                }
                                else
                                {
                                        f[i - p] = '1';
                                }
                                flag = 1;
                        }
                        else
                        {
                                if (f[i] != f[i - p])
                                {
                                        flag = 1;
                                }
                        }
                }
        }
        for (int i = 1; i <= n; i++)
        {
                if (f[i] == '.')
                {
                        f[i] = '1';
                }
        }
        if (!flag)
        {
                cout << "No" << endl;
        }
        else
        {
                printf("%s
", f + 1);
        }
}

View Code

构造题

直接搞个48*50的大块分成4个12*50的小块

再满足条件地在大块里面扣一个个1*1的小块即可

/*Huyyt*/
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int dir[8][2] = {{0, 1}, {1, 0}, {0, -1}, { -1, 0}, {1, 1}, {1, -1}, { -1, -1}, { -1, 1}};
const int mod = 1e9 + 7, gakki = 5 + 2 + 1 + 19880611 + 1e9;
const int MAXN = 1e5 + 5, MAXM = 1e5 + 5, N = 2e5 + 5;
const int MAXQ = 100010;
int sum[105];
char f[55][55];
int main()
{
        ios_base::sync_with_stdio(0);
        cin.tie(0);



        int a, b, c, d;
        cin >> a >> b >> c >> d;
        cout << 48 << " " << 50 << endl;
        for (int i = 1; i <= 48; i++)
        {
                for (int j = 1; j <= 50; j++)
                {
                        if (i <= 12)
                        {
                                f[i][j] = 'A';
                        }
                        else if (i <= 24)
                        {
                                f[i][j] = 'B';
                        }
                        else if (i <= 36)
                        {
                                f[i][j] = 'C';
                        }
                        else
                        {
                                f[i][j] = 'D';
                        }
                }
        }
        a--, b--, c--, d--;
        int dx = 14, dy = 1;
        for (int i = 1; i <= a; i++)
        {
                if (dy > 50)
                {
                        dy -= 50, dx += 2;
                }
                f[dx][dy] = 'A';
                dy+=2;
        }
        dx=26,dy=1;
        for (int i = 1; i <= b; i++)
        {
                if (dy > 50)
                {
                        dy -= 50, dx += 2;
                }
                f[dx][dy] = 'B';
                dy+=2;
        }
        dx=38,dy=1;
        for (int i = 1; i <= c; i++)
        {
                if (dy > 50)
                {
                        dy -= 50, dx += 2;
                }
                f[dx][dy] = 'C';
                dy+=2;
        }
        dx=2,dy=1;
                for (int i = 1; i <= d; i++)
        {
                if (dy > 50)
                {
                        dy -= 50, dx += 2;
                }
                f[dx][dy] = 'D';
                dy+=2;
        }
        for(int i=1;i<=48;i++)
        {
                for(int j=1;j<=50;j++)
                {
                        cout<<f[i][j];
                }
                cout<<endl;
        }
}

View Code

题意:

给你n块云(1<=n<=1e5) 每块云的长度是确定的L 月亮在原点每块云覆盖的区间为[Xi,Xi+L](-1e8<=Xi<=1e8) 初始每块云的速度是1或者-1

现在给你一个W_max 你可以选择一个速度W(-Wmax<=W<=Wmax)使得有一对云在某一个时间同时覆盖住月亮

问你可以由多少对

解:

http://codeforces.com/blog/entry/59968

把X轴上再加一条Y轴表示时间这样某一块云运动的轨迹就变成了一个斜着的条

如果两个云有交集的话在图上就变成有一个公共的小蓝方块

接着我们把W的速度转给月亮而不是给云这样云的速度就不变方便思考和计算

如果一对云可以同时遮到月亮的话小蓝方块与黄色月亮运动范围是有交集的即小蓝方块的最高点Y坐标大于下界斜率*当前横坐标

因为1<=W<=Wmax 所以月亮下界的斜率最小为1/Wmax 假设有一个往左的云u 有一个往右的云v 可以算出他们的小蓝块的最高点坐标为((Xu+Xv+L)/2,(Xu-Xv+L)/2)

接下来的要求即是解不等式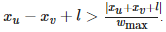把Xu+Xv+L分>=0与<0两种情况讨论即可

/*Huyyt*/
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int dir[8][2] = {{0, 1}, {1, 0}, {0, -1}, { -1, 0}, {1, 1}, {1, -1}, { -1, -1}, { -1, 1}};
const int mod = 1e9 + 7, gakki = 5 + 2 + 1 + 19880611 + 1e9;
const int MAXN = 1e5 + 5, MAXM = 1e5 + 5, N = 2e5 + 5;
const int MAXQ = 100010;
int n, l, w;
int x[MAXN], v[MAXN];
vector<int> pos, neg;
inline int div_floor(ll a, int b)
{
        if (b == 0)
        {
                if (a > 0)
                {
                        return INT_MAX;
                }
                else
                {
                        return INT_MAX * -1;
                }
        }
        if (a % b < 0)
        {
                a -= (b + a % b);
        }
        return a / b;
}
int main()
{
        scanf("%d %d %d", &n, &l, &w);
        for (int i = 0; i < n; i++)
        {
                scanf("%d %d", &x[i], &v[i]);
                if (v[i] == 1)
                {
                        pos.push_back(x[i]);
                }
                else
                {
                        neg.push_back(x[i]);
                }
        }
        sort(pos.begin(), pos.end()), sort(neg.begin(), neg.end());
        ll anser = 0;
        for (int v : neg)
        {
                auto barrier = lower_bound(pos.begin(), pos.end(), -v - l);
                int ansmax0 = div_floor(1LL * (v + l) * (w + 1) - 1, w - 1);
                int ansmax1 = div_floor(1LL * (v + l) * (w - 1) - 1, w + 1);
                anser += (upper_bound(pos.begin(), barrier, ansmax0) - pos.begin()) + (upper_bound(barrier, pos.end(), min(v, ansmax1)) - barrier);
        }
        printf("%lld
", anser);
}

View Code

待补

查看全文

相关阅读:
Boost.Bind的基础使用
 boost::bind
winform多线程方式登录代码整理
 shared_from_this 几个值得注意的地方
 [转]gtest使用
 以boost::function和boost:bind取代虚函数
 asio学习2: TCP服务器端:对准时间解析
 boost asio study
Asio学习1: TCP客户端:对准时间解析
 Shawn，别让我们失望

原文地址：https://www.cnblogs.com/Aragaki/p/9171404.html

Codeforces 989 P循环节01构造 ABCD连通块构造 思维对云遮月参考系坐标轴转换

Codeforces 989 P循环节01构造 ABCD连通块构造思维对云遮月参考系坐标轴转换