4.1 运算符介绍
运算符是一种特殊的符号,用于表示数据的运算、赋值和比较。
- 算数运算符
- 赋值运算符
- 比较运算符/关系运算符
- 逻辑运算符
- 位运算符
- 其他运算符
4.2 算数运算符
算数运算符是对 数值类型的变量进行运算的。比如:加减乘除
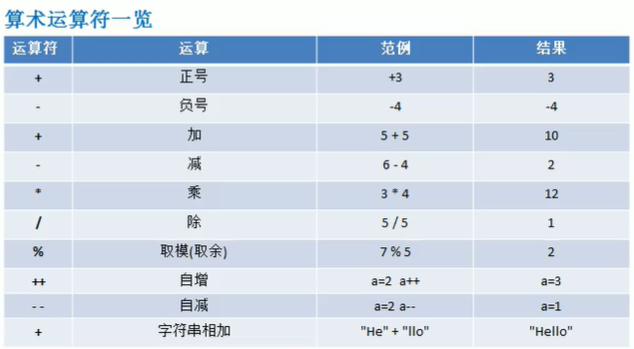
4.2.1 算数运算符一览表
案例:
+ 加
- 减
* 乘
% 取模
自增:++
自减:--
演示 / 的使用特点
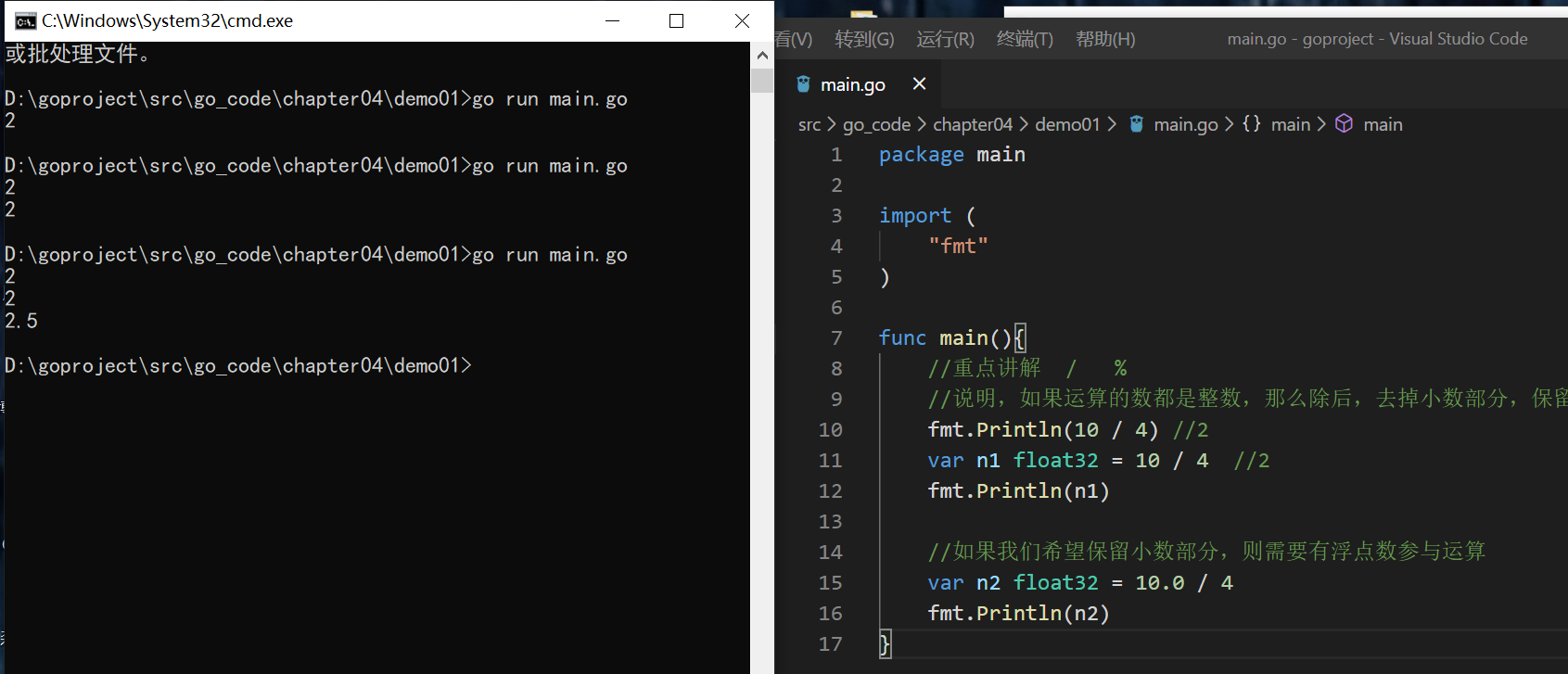
演示 % 的使用特点
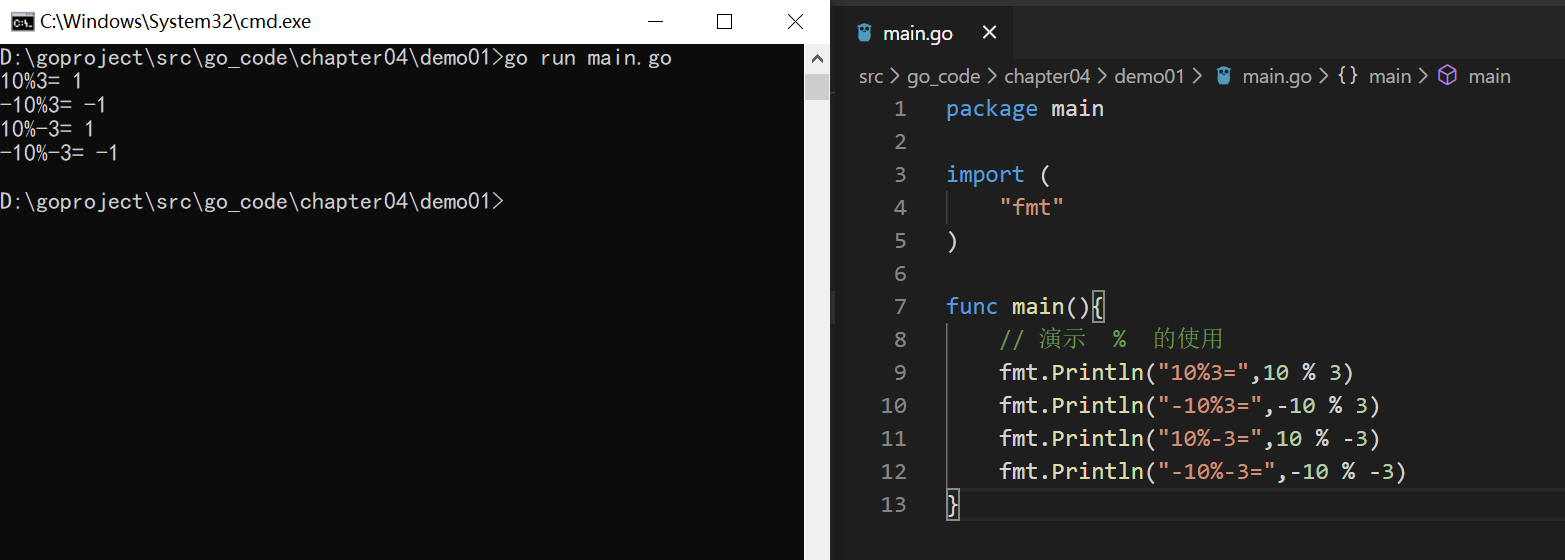
演示 ++ 和 -- 的使用
4.2.2 算数运算符使用的注意事项
- 对于除号 "/",它的整数除和小数除是有区别的:整数之间做除法时,只保留整数部分,而舍弃小数部分,例如:x:=19/5 结果是3
- 当一个数取模时,可以等价于a%b=a-a/b*b,这样我们可以考到取模的一个本质运算
- Golang的自增自减之呢个当作一个独立语言使用时,不能这样使用 b:=a++ 或者 b:=a--
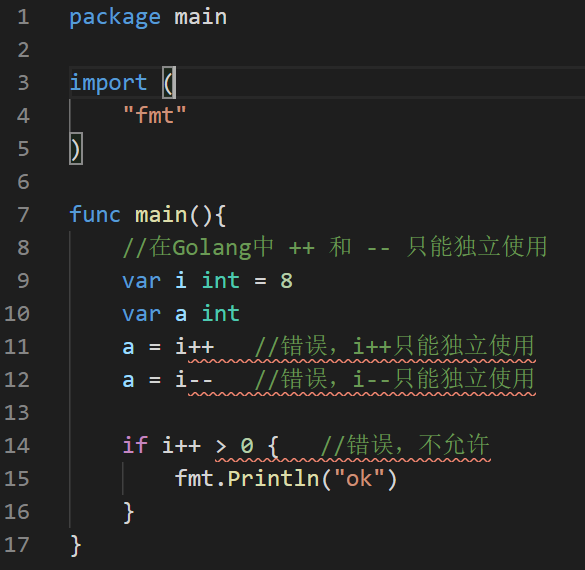
- Golang的++和--只能写在变量的后面,不能写在变量的前面,即:只有a++ a-- 没有 ++a --a
- Golang的设计者 去掉 c / java中的自增自减的容易混淆的写法,让Golang更加简洁,统一。(强制的)
测试
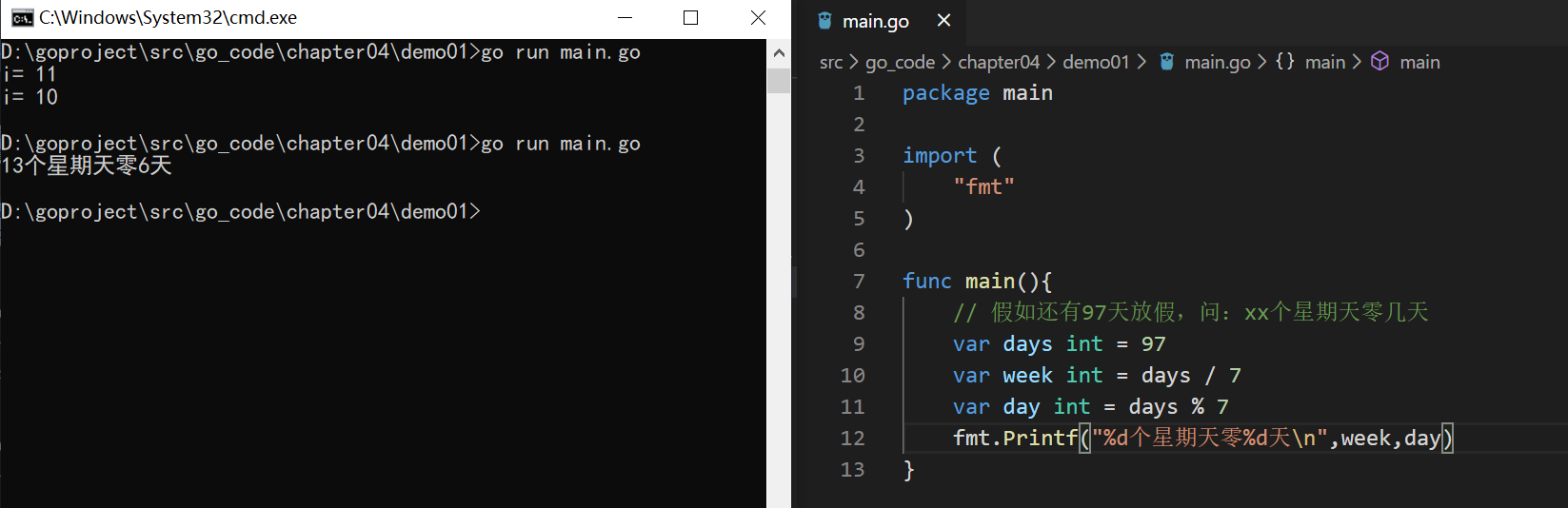
- 假如还有97天放假,问:xx个星期天零几天
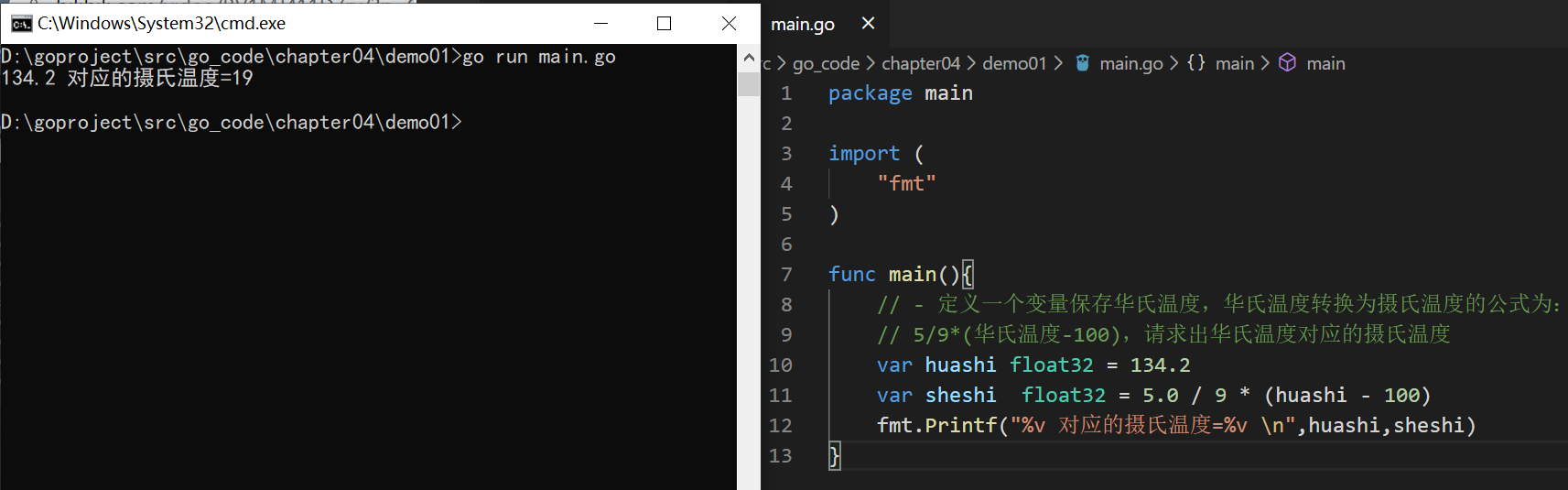
- 定义一个变量保存华氏温度,华氏温度转换为摄氏温度的公式为:5/9*(华氏温度-100),请求出华氏温度对应的摄氏温度
4.3 关系运算符(比较运算符)
4.3.1 基本介绍
- 关系运算符的结果都是bool型,也就是要么算是true,要么是false
- 关系表达式经常用在 if结构的条件中或循环结构的条件中
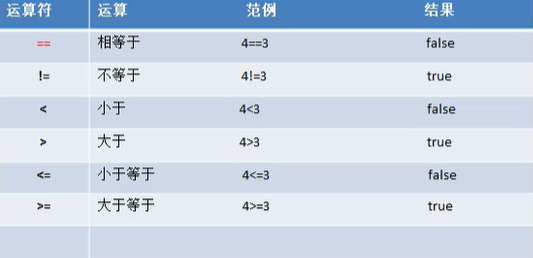
4.3.2 关系运算符一览
4.3.3 使用细节说明
- 关系运算符的结果都是bool型,也就是要么是tru,e要么是false
- 关系运算符组成懂得表达式,我们称之为 关系表达式 a>b
- 比较运算符 “==” 不能误写成 ”=“
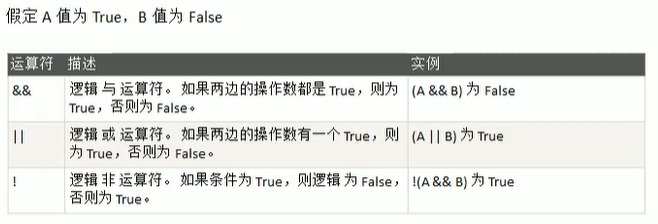
4.4 逻辑运算符
4.4.1 基本介绍
用于连接多个条件(一般来说就是关系表达式),最终的结果也是一个bool值。
4.4.2 逻辑运算符一览表
4.4.3 注意事项和细节说明
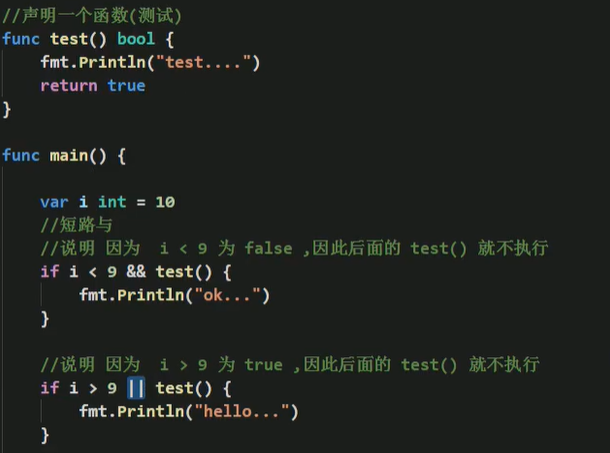
- && 也叫短路与,如果第一个条件为false,则第二个条件不会判断,最终结果为false
- || 也叫短路或,如果第一个条件为true,则第二个条件不会判断,最终结果为true
4.5 赋值运算
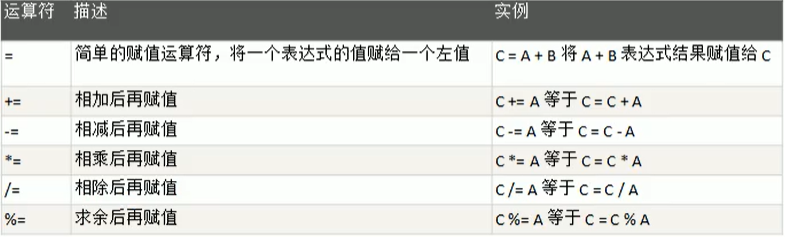
4.5.1 基本介绍
赋值运算符就是将某个运算后的值,赋给指定的变量。
4.5.2 赋值运算符的分类
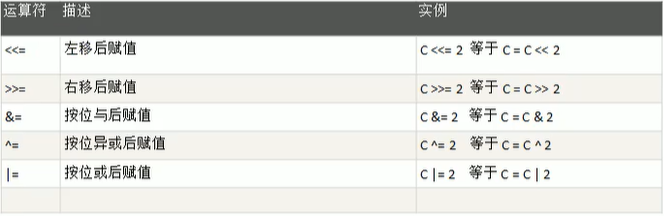
上图说明:这部分的赋值运算符涉及到二进制相关知识
4.5.3 案例
4.5.4 赋值运算符的特点
- 运算符从右往左
- 赋值运算符懂得左边只能变量,右边可以是变量、表达式,常量值
- 复合运算符等价于 a + = 3 等价于 a = a + 3
面试题
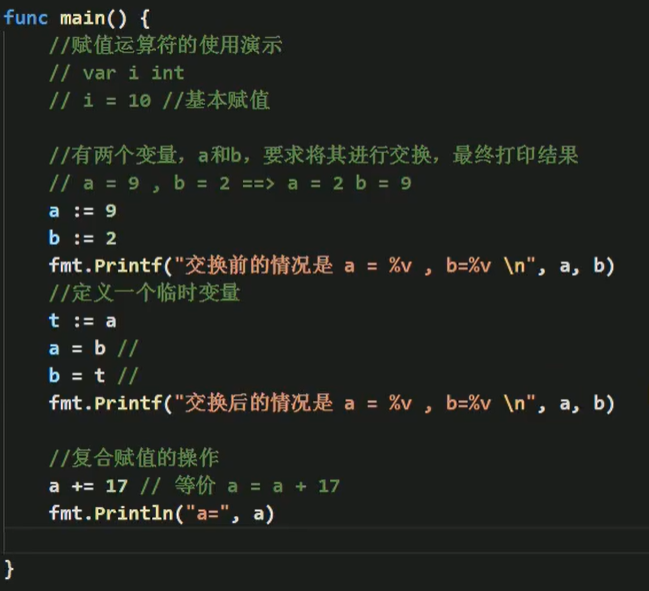
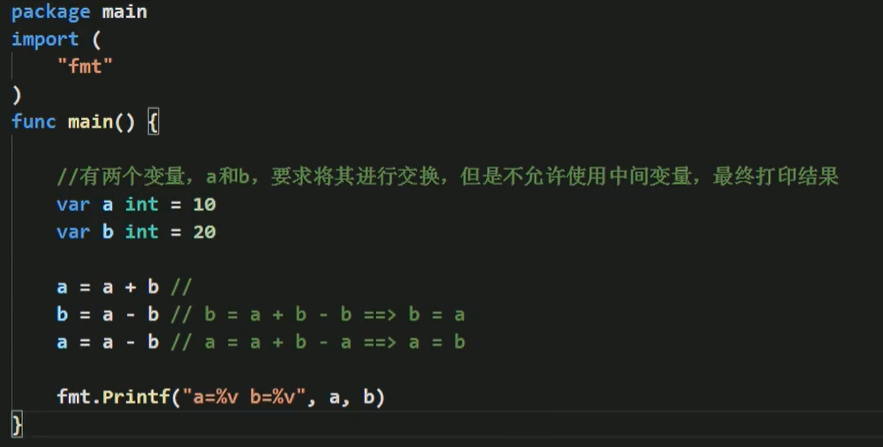
有两个变量,a和b,要求将其进行交换,但是不允许使用中间变量,最终打印结果。
4.6 运算符优先级
- 运算符有不同的E优先级,所谓优先级就是表达式运算中的运算顺序,如下表,上一行运算符总优于下一行

- 只有单目运算符、赋值运算符是从右向左运算的
- 大致顺序整理
- 括号,++ --
- 单目运算
- 算术运算符
- 移位运算
- 关系运算符
- 位运算符
- 逻辑运算符
- 赋值运算符
- 逗号
4.7 位运算符

4.8 其他运算符
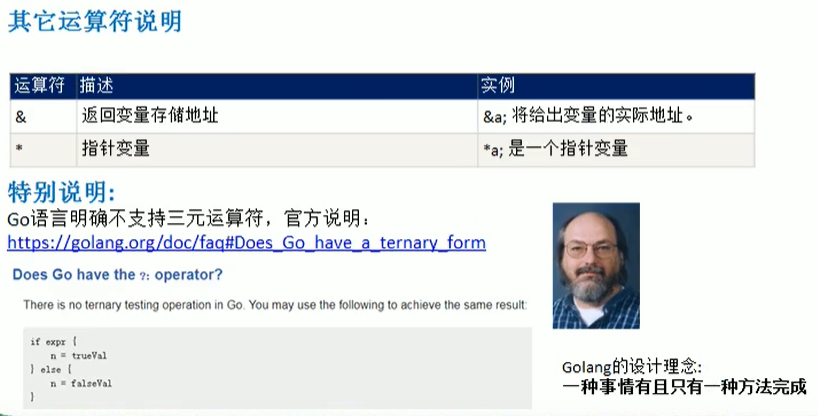
案例:
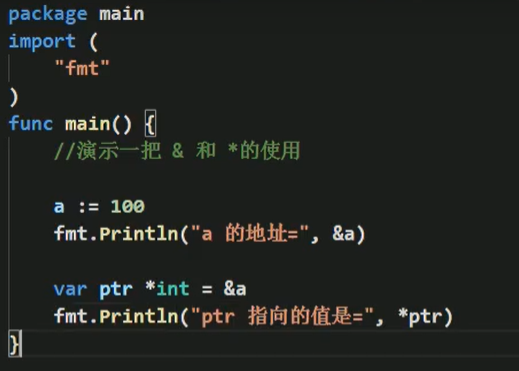
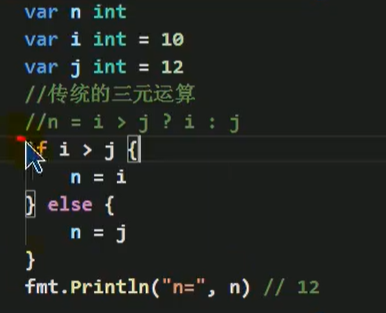
练习题
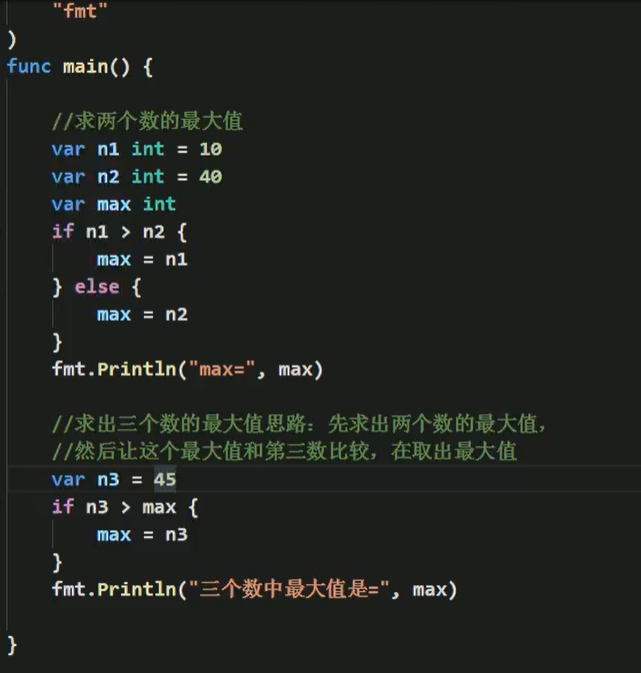
4.9 键盘输入语句
4.9.1 介绍
在编程中,需要接收用户输入的数据,就可以使用键盘输入语句来获取 InputDemo.go
4.9.2 步骤
- 导入 fmt包
- 调用 fmt 包的 fmt.Scanln() 或者 fmt.Scanf()
4.9.3 案例演示
要求:可以从控制台接收用户信息 (姓名,年龄,薪水,是否通过)
- 使用 fmt.Scanln() 获取

- 使用 fmt.Scanf() 获取

4.10 进制
4.10.1 进制介绍
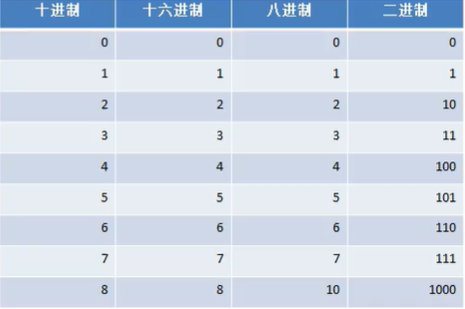
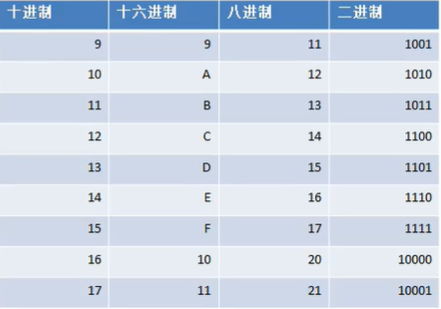
对于整数。有四种表示方式:
-
二进制 :0,1 满2进1
在Golang中,不能直接使用二进制来表示一个整数,它沿用了 c 的特点
-
十进制:0-9,满10进1
-
八进制:0-7,满8进1
-
十六进制:0-9及A-F,满16进1 以0x或0X开头表示,此处的A-F不区分大小写

进制图示:
4.10.2 进制的转换介绍
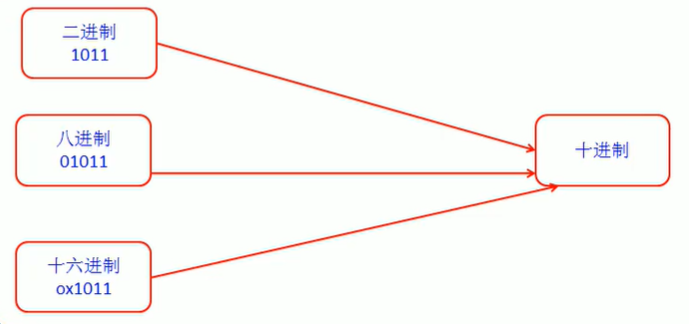
第一组 (其它进制转十进制)
- 二进制转十进制
- 八进制转十进制
- 十六进制转十进制
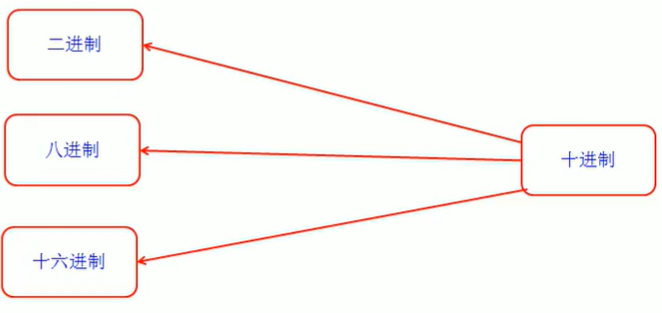
第二组 (十进制转其它进制)
- 十进制转二进制
- 十进制转八进制
- 十进制转十六进制
第三组 (二进制转其它进制)
- 二进制转八进制
- 二进制转十六进制
- 示意图
第四组 (其它进制转二进制)
- 八进制转二进制
- 十六进制转二进制
- 示意图
4.10.3 其它进制转十进制
4.10.3.1 二进制如何转十进制
规则:从最低位开始(右边的),将每位上的数提取出来,乘以2的(位数-1)次方,然后求和
案例:请将二进制:1011转换成十进制的数
1011 = 1 * 2的0次方 + 1 * 2的1次方 + 0 * 2的2次方 + 1 * 2的3次方 = 1 + 2 + 0 + 8 = 11
4.10.3.2 八进制转换成十进制
规则:从最低位开始(右边的),将每位上的数提取出来,乘以8的(位数-1)次方,然后求和
案例:请将 0123转化为十进制的数
0123 = 3 * 1 + 2 * 8 + 1 * 8 * 8 = 3 + 16 + 64 = 83
4.10.3.3 十六进制转十进制
规则: 从最低位开始(右边的),将每位上的数提取出来,乘以16的(位数-1)次方,然后求和
案例:请将 0x34A 转成十进制的数
0x34A = 10 * 1 + 4 * 16 + 3 * 16 * 16 = 10 + 64 + 768 = 842
4.10.4 十进制转其它进制
4.10.4.1 十进制转换成二进制
规则:将该数不断除以2,直到商为0为止,然后将每步得到的余数倒过来,就是对应的二进制
案例:请将56转换成二进制
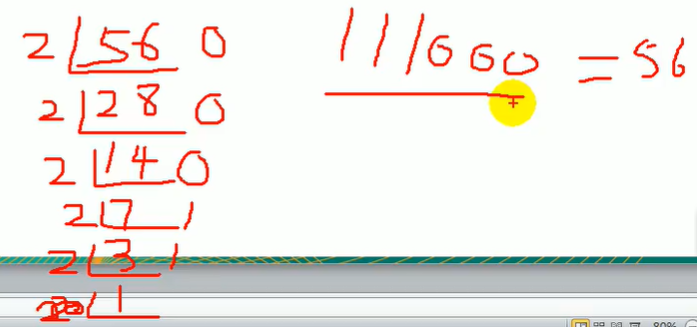
4.10.4.2 十进制转换八进制
规则:将该数不断除以8,直到商为0为止,然后将每步得到的余数倒过来,就是对应的八进制
案例:请将156转换成八进制
156 除 8 商19 余4
19 除 8 商2 余3
3 除 8 商0 余2
156的八进制为:234
4.10.4.3 十六进制转换八进制
规则:将该数不断除以16,直到商为0为止,然后将每步得到的余数倒过来,就是对应的十六进制
案例:请将356转换成八进制
356 = 0X164
4.10.5 二进制转八进制,十六进制
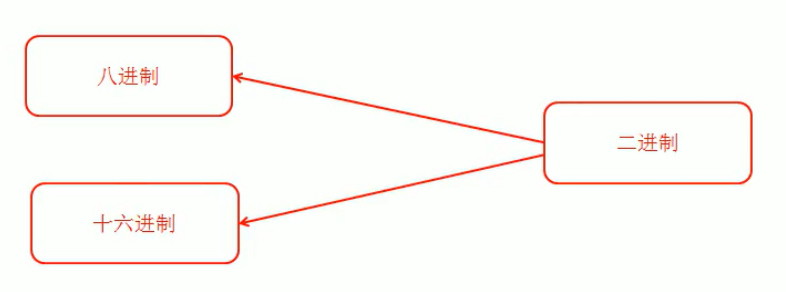
4.10.5.1 二进制转八进制
规则:将二进制数每三位一组(从低位开始组合),转成对应的八进制数即可。
案例:请将二进制:11010101转成八进制
11010101 = 325
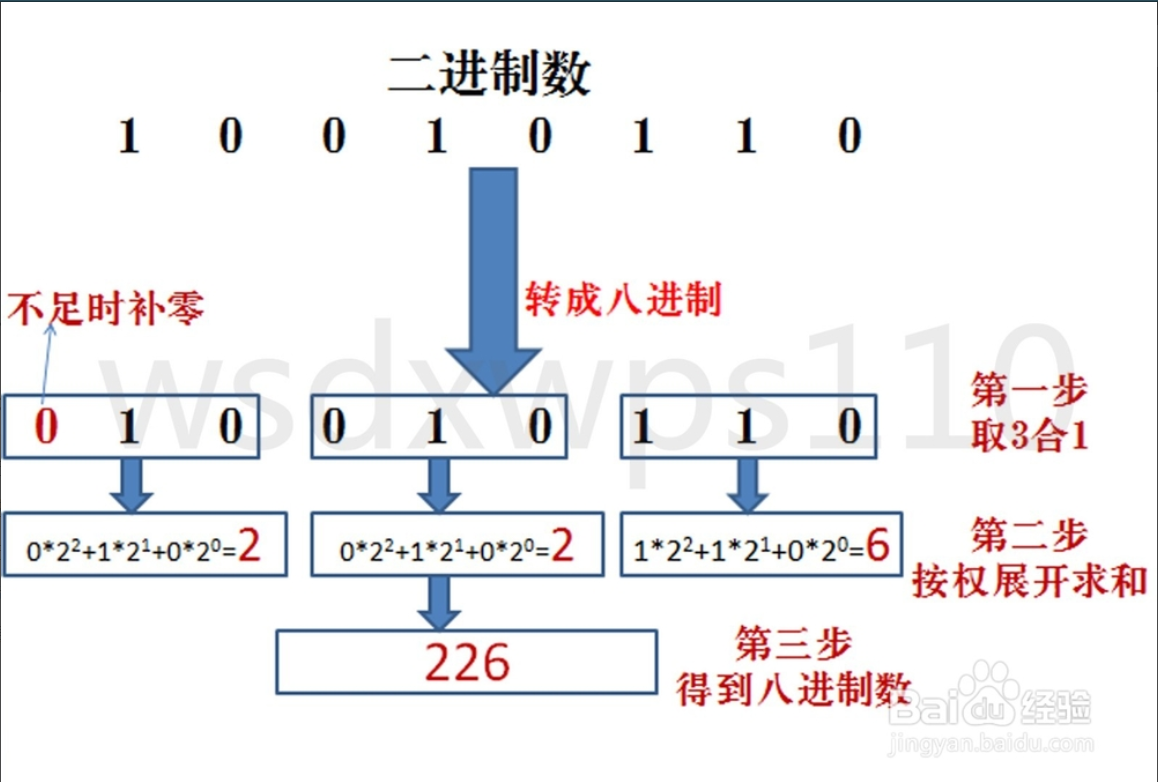
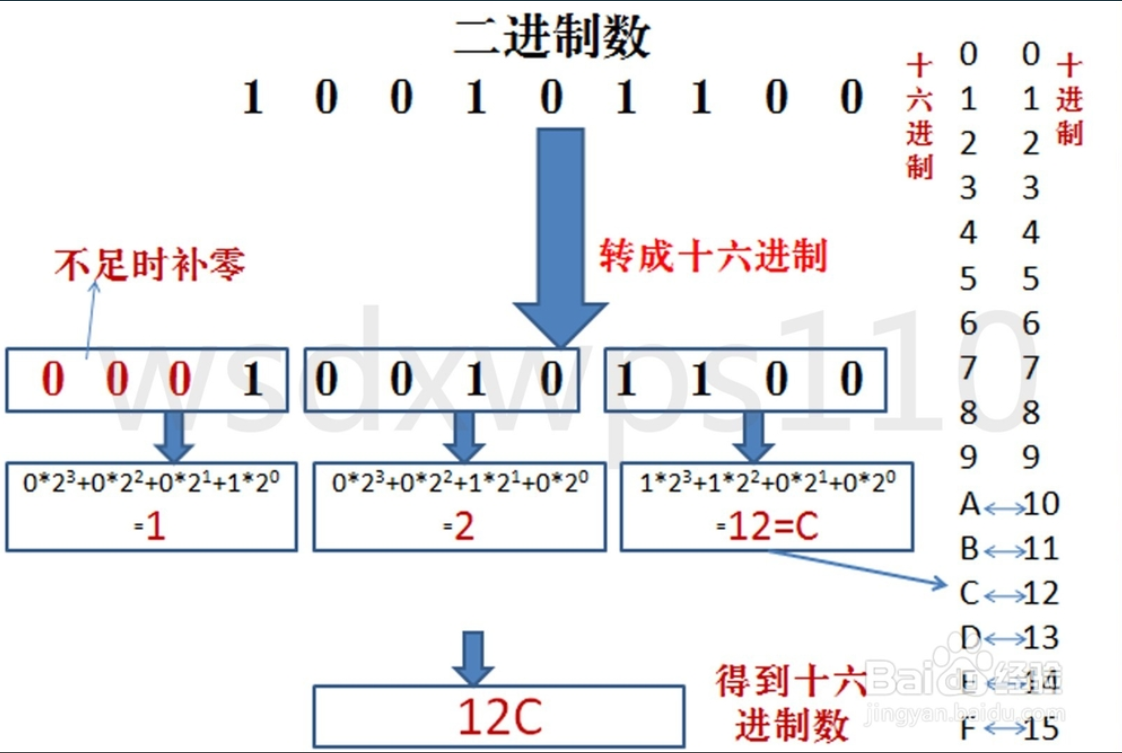
4.10.5.2 二进制转十六进制
规则:将二进制数每四位一组(从低位开始组合),转成对应的十六进制数即可。
案例:请将二进制:11010101 转成十六进制
11010101 = 0XD5
4.10.6 八进制、十六进制转二进制
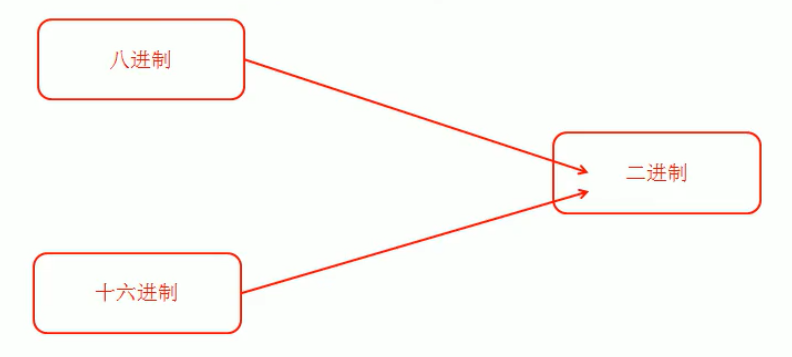
4.10.6.1 八进制转二进制
规则:将八进制每一位,转成对应的一个3位的二进制数即可
案例:请将0237转成二进制 0237=10011111
4.10.6.2 十六进制转二进制
规则:将十六进制每一位,转成对应的一个4位的二进制数即可
案例:请将0x 237转成二进制 0x237 = 1000110111
4.11 位运算
4.11.1 原码、反码、补码
对于有符号的而言:
- 二进制的最高位是符号位:0表示正数,1表示负数,首位表示符号位
- 正数的原码、反码、补码都一样
- 负数的反码=它的原码符号位不变,其他位取反(0->1,1->0)
- 1==> 原码[0000 0001] 反码[0000 0001] 补码[0000 0001]
- -1 ==> 原码[1000 0001] 反码[1111 1110] 补码[1111 11111]
- 负数的补码=它的反码+1
- 0的反码,补码都是0
- 在计算机运算的时候,都是以补码的方式来运算的
4.11.2 位运算符和移位运算符
4.11.2.1 Golang中有3个位运算
分别是 按位与&、按位或|、按位异或^ 它们的运算规则是:
按位与& : 两个全为1,结果为1,否则为0
按位或| : 两个有一个为1,结果为1,否则为0
按位异或^ : 两个一个为0,一个为1,结果为1,否则为0
案例
2&3
2 的补码 0000 0010
3 的补码 0000 0011
2&3 0000 0010 => 2
2|3=?
2 的补码 0000 0010
3 的补码 0000 0011
2|3 0000 0011 => 3
2^3
2 的补码 0000 0010
3 的补码 0000 0011
2^3 0000 0001 =>1
-2^2
-2 的原码 1000 0010 =》反码 1111 1101 => 补码 1111 1110
1111 1110
2 的补码 0000 0010
-2^2 1111 1100 (补码) ===》 原码
1111 1100 =》 反码 1111 1011 =》 原码 1000 0100 ==》 -4
4.11.2.2 Golang中有2个移位运算符
>> << 右移和左移,运算规则
右移运算符:低位溢出,符号位不变,并用符号位补溢出的高位
左移运算符:符号位不变,低位补0
案例
a:=1 >> 2 // 0000 0001 >> 0000 0000 >> 0
c:1 << 2 //0000 0001 >> 0000 0100 >> 4