http://poj.org/problem?id=3414
题目描述:
给你两个容器,分别能装下A升水和B升水,并且可以进行以下操作
FILL(i) 将第i个容器从水龙头里装满(1 ≤ i ≤ 2);
DROP(i) 将第i个容器抽干
POUR(i,j) 将第i个容器里的水倒入第j个容器(这次操作结束后产生两种结果,一是第j个容器倒满并且第i个容器依旧有剩余,二是第i个容器里的水全部倒入j中,第i个容器为空)
现在要求你写一个程序,来找出能使其中任何一个容器里的水恰好有C升,找出最少操作数并给出操作过程
Input
有且只有一行,包含3个数A,B,C(1<=A,B<=100,C<=max(A,B))
Output
第一行包含一个数表示最小操作数K
随后K行每行给出一次具体操作,如果有多种答案符合最小操作数,输出他们中的任意一种操作过程,如果你不能使两个容器中的任意一个满足恰好C升的话,输出“impossible”
Sample Input
3 5 4
Sample Output
6 FILL(2) POUR(2,1) DROP(1) POUR(2,1) FILL(2) POUR(2,1)
面向题解的思路:
我们需要找使得某个容器里面的水有C升,并按照题目的操作步骤的话,就是一个一个的尝试。看的大部分题解都是用广搜做的。
很麻烦的一道题,但总体来看就是一个有六个入口的bfs问题,知道了这个状态的变换,以及结束的条件:尝试遍历无结果以及找到解。根据这些就可以有个大体的轮廓了。
六个入口分别是:fill (1)
fill (2)
drop (1)
drop (2)
pour (1)
pour (2)
不仅如此,我们变换后状态还要判断在队列中是否已经存在或是有过这种状态。(防止出现多余的枝)
于是考虑建立一个数组 all 来记录。
还有就是当前的状态不能影响之前的状态。
第一个搜索得到的解一定是最优解,或是最优解的其中一个。搜索的深度就代表着达到某个解的最小步数。
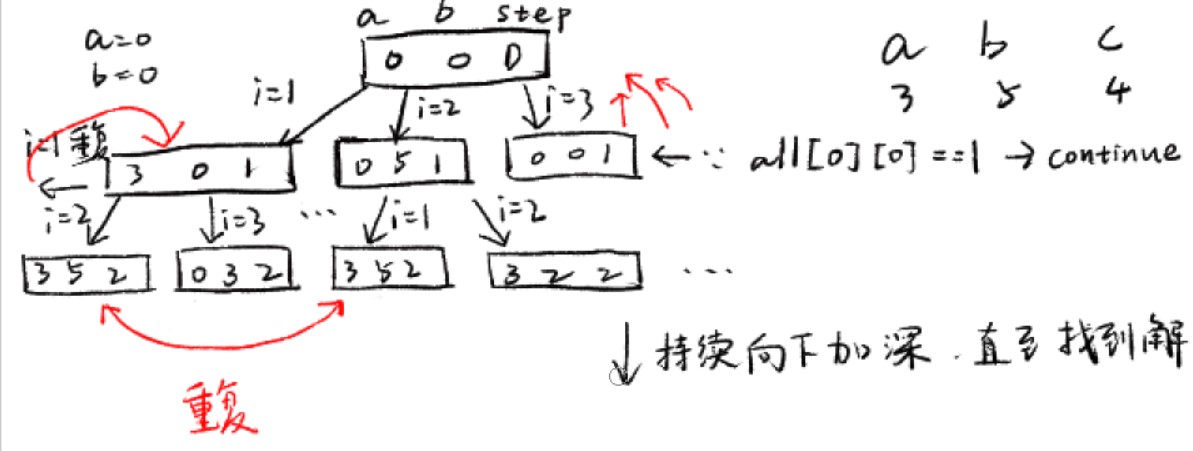
而当我们一层层往下搜索时,大概能够得到一个这样的搜索:
(哎呀图太大了。。。)
代码在这,想到再补充,主要思路和学长的题解一样。
1 #include <bits/stdc++.h> 2 3 #define N 100010 4 #define maxn 200010 5 6 using namespace std; 7 8 typedef long long int ll; 9 10 int a, b, c; 11 typedef struct node{ 12 int A; //某刻A中水量 13 int B; //某刻B中水量 14 int step; //总数 15 int temp[N]; //记录步骤 16 }can; 17 can x; 18 int all[110][110]={0}; //记录遍历到的状态 19 void bfs(){ 20 queue<can> now; 21 now.push(x); 22 can y; 23 while(!now.empty()){ 24 y=now.front(); 25 now.pop(); 26 //A或B容器中有一个满足题意 27 if(y.A==c || y.B==c){ 28 printf("%d ", y.step); 29 for(int i=0; i<y.step; i++){ 30 switch(y.temp[i]){ 31 case 1: printf("FILL(1) "); break; 32 case 2: printf("FILL(2) "); break; 33 case 3: printf("DROP(1) "); break; 34 case 4: printf("DROP(2) "); break; 35 case 5: printf("POUR(1,2) "); break; 36 case 6: printf("POUR(2,1) "); break; 37 } 38 } 39 return ; //可以把这里去掉看全部的解 40 } 41 else{ 42 can save; //替换一下y 43 //六个入口的bfs 44 for(int i=1; i<=6; i++){ 45 save=y; 46 save.temp[save.step++]=i; //记录走到当前的总步骤 47 switch(i){ 48 case 1: save.A=a; break; 49 case 2: save.B=b; break; 50 case 3: save.A=0; break; 51 case 4: save.B=0; break; 52 case 5:{ 53 if(save.A+save.B>b) { 54 save.A=save.A-(b-save.B); 55 save.B=b; 56 } 57 else{ 58 save.B=save.A+save.B; 59 save.A=0; 60 } 61 } break; 62 case 6:{ 63 if(save.A+save.B>a){ 64 save.B=save.B-(a-save.A); 65 save.A=a; 66 } 67 else{ 68 save.A=save.A+save.B; 69 save.B=0; 70 } 71 } break; 72 } 73 //检测状态是否重复 74 if(all[save.A][save.B]) continue; 75 //否则放入队列中 76 now.push(save); 77 all[save.A][save.B]=1; 78 } 79 } 80 } 81 printf("impossible "); 82 } 83 int main() 84 { 85 scanf("%d%d%d", &a, &b, &c); 86 x.A=x.B=0; 87 x.step=0; 88 all[0][0]=1; 89 bfs(); 90 return 0; 91 }