最小生成树 (Minimum Spanning Tree,MST) --- Kruskal算法

本文链接:http://www.cnblogs.com/Ash-ly/p/5409265.html

引导问题：

　　假设要在N个城市之间建立通信联络网，则连通N个城市只需要N - 1条线路。这时，自然会考虑这样一个问题，如何在最省经费的前提下建立这个通信网。

基于问题所建立的定义：

　　可以用联通网来表示N个城市以及N个城市之间可能设置的连通线路，其中网的顶点表示城市，边表示两城市之间的线路，赋予边的权值表示相应的代价。对于N个顶点的连通网可以建立许多不同的生成树，每一棵生成树都可以是一个通信网。现在，要选择这样一颗生成树，也就是使总的耗费最少，这个问题就是构造连通网的的最小代价生成树的问题，即最小生成树问题。一颗生成树的代价就是树上各边的代价之和。

算法：

　　假设；连通网N = (V, {E})，则令最小生成树的初始状态为只有N个顶点而无边的非连通图T = (V, {})，图中每个顶点自成一个连通分量。在E中选择代价最小的边，若该边依附的顶点落在不同的连通分量上，则将该边加入到T中，否则舍去此边，选择下一条代价最小的边。以此类推，直至所有顶点都在同一个连通分量上为止。

　　时间复杂度:O(ElogE)，适合点多边少的稀疏图。

用图来描述：

初始图 N　　　　　　　　　　　　　　　　　　　　　　初始图 T

 　　

求此图的最小生成树。

第一步：先给这些边排序。

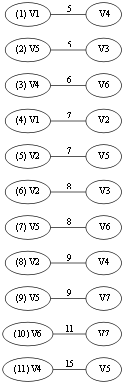
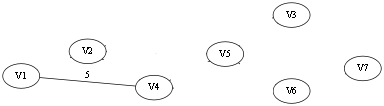
然后选择第(1)条边V1 -- V4，第一条边的两端属于两个连通分量，所以可以加入 T 中

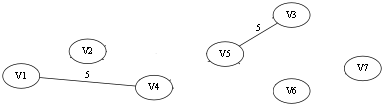
继续选择第(2)条边V5 -- V3，第二条边的两端也属于两个连通分量，所以也可以加入 T 中

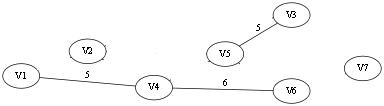
选择第(3)条边V4 -- V6，第三条边的两端也属于两个连通分量，加入 T 中

选择第四条边V1 -- V7，同样属于两个连通分量，加入 T 中

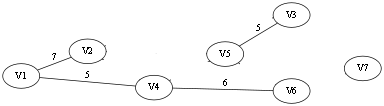
选择第五条边，V2 -- V5，也属于两个连通分量，加入 T 中

选择第六条边V2 -- V3后会变成这样

很明显，第六条边的两端是属于一个连通分量的，所以舍弃继续选择第七条边V5 -- V6

同样，第七条边的两端属于同一个连通分量，所以舍弃，选择第八条变条边V2 -- V4

和上面两条边的状况一样，所以继续舍弃，选择第九条边，V5 -- V7

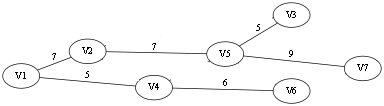
到此为止，所有的点都被连通到了一起，图中仅存在一个连通分量，算法停止，T 中所选择的边和原先的点构成的图就是要找的最小生成树。

具体实现:

　　判断是否属于一个连通分量可以用并查集实现。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <cctype>
#include <algorithm>
#include <queue>
#include <stack>
#include <map>
#include <set>
using namespace std;

const int MAXN = 2e3+ 3;
int pre[MAXN];
int m,n;

int Find(int x)     //并查集
{
    return x == pre[x] ? x :(pre[x] = Find(pre[x]));
}

struct Node   //储存数据
{
    int u, v, w;
}cy[103];

int mycmp(Node a,Node b)
{
    return a.w < b.w;
}

void mst()
{
    for(int i = 0 ; i < 102; i++)
        pre[i] = i;
}

int kru()
{
    int ans = 0;
    int cnt = 0;
    sort(cy + 1, cy + n + 1, mycmp);  //对边进行升序排序
    for(int i = 1; i <= n; i++)       //从最小的那条边开始寻找
    {
        int fv = Find(cy[i].v);   
        int fu = Find(cy[i].u);
        if(fv != fu)               //如果不属于同一个连通分量就把当前这条比较小的边加进去
        {
            pre[fv] = fu;
            ans += cy[i].w;
            cnt ++;
        }
        if(cnt == m -1)      //构成了最小生成树
        {
            return ans;
            break;
        }
    }
    return -1;
}

int main()
{
    //freopen("in.cpp","r",stdin);
    while(~scanf("%d%d",&n,&m) && n)
    {
        mst();
        for(int i = 1; i <= n; i++)
            scanf("%d%d%d",&cy[i].u, &cy[i].v, &cy[i].w);
        int ans = kru();
        if(ans != -1)
            printf("%d
",ans);
        else
            printf("?
");
    }
    return 0;
}