ACM题目————网格动物

Lattice animal is a set of connected sites on a lattice. Lattice animals on a square lattice are especially popular subject of study and are also known as polyominoes. Polyomino is usually represented as a set of sidewise connected squares. Polyomino with n squares is called n-polyomino. In this problem you are to find a number of distinct free n-polyominoes that fit into rectangle w×h. Free polyominoes can be rotated and flipped over, so that their rotations and mirror images are considered to be the same. For example, there are 5 different pentominoes (5-polyominoes) that fit into 2×4 rectangle and 3 different octominoes (8-polyominoes) that fit into 3×3 rectangle.

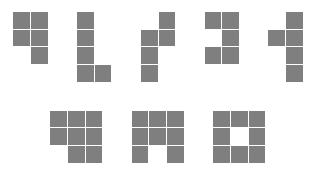
Input 

The input file contains several test cases, one per line. This line consists of 3 integer numbers n, w, and h ( 1n10, 1w, hn).

Output 

For each one of the test cases, write to the output file a single line with a integer number -- the number of distinct free n-polyominoes that fit into rectangle w×h.

Sample Input 

5 1 4
5 2 4
5 3 4
5 5 5
8 3 3

Sample Output 

0
5
11
12
3

输入n，w，h （1<=n<=10,1<=w,h<=n），求能放在w*h网格里的不同的n连块的个数(注意,平移，旋转，翻转后相同的算作同一种)。例如，2*4里的5连块有5种(第一行)，而3*3里的8连块有以下3种(第二行)。

难点：

1.以每个格子来扩展。先枚举1连块，在对1连块的每个格子的4个方向进行扩展，枚举2连块，依次类推。

2.将n连块表示成n个格子的集合，将所有的n连块又表示成集合，判重任务交给set.

3.判重时要将n连块进行8个方向的旋转，并且每个n连块需要规范化(左下角的格子在(0,0)).

4.得到n连块后判断是否能放进w*h的网格中，由于n连块已经规范化，得到n连块的格子最大x,y坐标，即能盛下该n连块的长和宽。

#include <cstdio>
#include <set>
#include <algorithm>
using namespace std;
#define maxn 10
// 代表一个网格节点
typedef struct cell
{
	int x, y;	//网格节点的坐标

	// 构造函数
	cell(int x, int y)
	{
		this->x = x;
		this->y = y;
	}

	bool operator < (const struct cell& a) const
	{
		return x < a.x || (x == a.x && y < a.y);
	}
}cell;

// 一个Polyomino就是一堆cell的集合
typedef set<cell> poly;

// poly_set[i]代表有i个cell的poly集合
set<poly> poly_set[maxn+1];

// answer[n][w][h]的答案
int answer[maxn+1][maxn+1][maxn+1];

void gen_poly();
void check_poly(const poly& this_p, cell& this_c);
poly normalize(poly& p);
poly rotate(poly& p);
poly flip(poly& p);


int main()
{
	// 生成所有poly
	gen_poly();

//	printf("here
");
	int n, w, h;
	while(scanf("%d %d %d", &n, &w, &h) == 3)
	{
		printf("%d
", answer[n][w][h]);
	}
	return 0;
}

int dic_x[4] = {-1,0,1,0};
int dic_y[4] = {0,1,0,-1};

// 生成所有poly
void gen_poly()
{
	for(int i = 1; i <= maxn; i++)
		poly_set[i] = set<poly>();

	// 先生成有1个cell的poly
	poly p1;
	p1.insert(cell(0,0));
	poly_set[1].insert(p1);

	// 分别根据有i-1个cell的poly集合来生成有i个cell的poly集合
	for(int i = 2; i <= maxn; i++)
	{
		// 对每个poly中的每个cell尝试在不同的四个方向增加一个cell
		for(set<poly>::iterator p = poly_set[i-1].begin(); p != poly_set[i-1].end(); p++)
		{
			for(poly::const_iterator q = p->begin(); q != p->end(); q++)
			{
				for(int j = 0; j < 4; j++)
				{
					cell new_c(q->x+dic_x[j], q->y+dic_y[j]);
//					cell new_c;
					if(p->find(new_c) == p->end())
					{
						// 检查形成的这个poly是否存在，如果不存在就加入
						check_poly(*p, new_c);
					}

				}
			}
		}
	}

	// 对所有n,w,h生成答案
	for(int i = 1; i <= maxn; i++)
	{
		for(int w = 1; w <= i; w++)
		{
			for(int h = 1; h <= i; h++)
			{
				int count = 0;
				for(set<poly>::iterator p = poly_set[i].begin(); p != poly_set[i].end(); p++)
                		{
					int max_x = p->begin()->x, max_y = p->begin()->y;
					for(poly::iterator q = p->begin(); q != p->end(); q++)
					{
						if(max_x < q->x)
							max_x = q->x;
						if(max_y < q->y)
							max_y = q->y;
					}

					if(min(max_x, max_y) < min(w, h) && max(max_x, max_y) < max(w, h))
					{
						count++;
					}
				}
/*				if(count != 0)
					printf("answer[%d][%d][%d] = %d
", i, w, h, count);
*/				answer[i][w][h] = count;
			}
		}
	}
}


// 检查形成的这个poly加上这个cell是否存在，如果不存在就加入
void check_poly(const poly& this_p, cell& this_c)
{
	poly p = this_p;
	p.insert(this_c);
	// 规范化到最小点为(0,0)
	p = normalize(p);

	int n = p.size();
	// 检查旋转的8个方向是否存在，如果不存在就加入到poly集合
	for(int i = 0; i < 4; i++)
	{
		if(poly_set[n].find(p) != poly_set[n].end())
			return;
		// 对该poly向右旋转90度
		p = rotate(p);
	}
	// 将该poly向下反转180度
	p = flip(p);
	for(int i = 0; i < 4; i++)
        {
                if(poly_set[n].find(p) != poly_set[n].end())
                        return;
                // 对该poly向右旋转90度
                p = rotate(p);
        }
	poly_set[n].insert(p);

}

// 规范化到最小点为(0,0)
poly normalize(poly& p)
{
	poly this_p;
	int min_x = p.begin()->x, min_y = p.begin()->y;
	for(poly::iterator q = p.begin(); q != p.end(); q++)
	{
		if(q->x < min_x)
			min_x = q->x;
		if(q->y < min_y)
			min_y = q->y;
	}
	for(poly::iterator q = p.begin(); q != p.end(); q++)
        {
		this_p.insert(cell(q->x-min_x,q->y-min_y));
        }
	return this_p;
}

// 对该poly向右旋转90度
poly rotate(poly& p)
{
	poly this_p;
	for(poly::iterator q = p.begin(); q != p.end(); q++)
        {
                this_p.insert(cell(q->y,-q->x));
        }
        return normalize(this_p);
}


// 将该poly向下反转180度
poly flip(poly& p)
{
	poly this_p;
        for(poly::iterator q = p.begin(); q != p.end(); q++)
        {
                this_p.insert(cell(q->x,-q->y));
        }
        return normalize(this_p);
}