【二叉树】二叉树遍历总结

　　节点定义如下

// Definition for a binary tree node.
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
}

　　前序遍历：

　　若二叉树为空，则空操作返回，否则：

1. 访问根节点
2. 前序遍历根节点的左子树
3. 前序遍历根节点的右子树  

　　中序遍历：

　　若二叉树为空，则空操作返回，否则：

1. 中序遍历根节点的左子树
2. 访问根节点
3. 中序遍历根节点的右子树

　　后序遍历：

　　若二叉树为空，则空操作返回，否则：

1. 后序遍历根节点的左子树
2. 后序遍历根节点的右子树
3. 访问根节点　　

 　　层序遍历：

　　其中后序遍历可以看作是和前序遍历是对称的，所以从根节点开始先遍历右子树，再遍历左子树，不过要把最后的遍历输出翻转过来。所以后序遍历的代码和前序遍历的代码基本一致，只是左右子树的访问顺序不同。

1. 递归方法

　　前序遍历：

void preorderTraversal(TreeNode* root, vector<int>& nums) {
    if(!root) return;
    nums.push_back(root->val); // 访问根节点
    preorderTraversal(root->left); // 前序遍历左子树
    preorderTraversal(root->right); // 前序遍历右子树
}

　　中序遍历：

void inorderTraversal(TreeNode* root, vector<int>& nums) {
    if(!root) return;   
    inorderTraversal(root->left, nums); // 中序遍历左子树
    nums.push_back(root->val);          // 访问根节点
    inorderTraversal(root->right, nums); // 中序遍历右子树
} 

　　后序遍历：

void postorderTraversal(TreeNode* root, vector<int>& nums) {
    if(!root) return;   
    postorderTraversal(root->left, nums); // 后序遍历左子树
    postorderTraversal(root->right, nums); // 后序遍历右子树
    nums.push_back(root->val);            // 访问根节点
}

 　  层序遍历：

vector<vector<int>> levelOrder(TreeNode* root) {
    vector<vector<int> > res;
    levelorder(root, 0, res);
    return res;
}
void levelorder(TreeNode *root, int level, vector<vector<int> > &res) {
    if (!root) 
        return;
    if (res.size() == level) 
        res.push_back({});
    
    res[level].push_back(root->val);
    
    if (root->left) 
        levelorder(root->left, level + 1, res);
    if (root->right) 
        levelorder(root->right, level + 1, res);
}

2.迭代方法（使用栈）

　　

　　前序遍历 1)：

void preorderTraversal(TreeNode* root, vector<int>& nums) {
    TreeNode* cur = root;
　　stack<TreeNode* > st; 

    while (cur || !st.empty()) {
        if (cur) {
            st.push(cur);
            nums.push_back(cur->val);
            cur = cur->left;
        } else {
            cur = st.top();
            st.pop();
            cur = cur->right;
        }
     }
}

　　前序遍历 2)：

void preorderTraversal(TreeNode* root, vector<int>& nums) {
    TreeNode* cur = root;
　　stack<TreeNode* > st; 

    while (cur || !st.empty()) {
        if (!cur) {                           // 根节点为空，则需要返回上一级
            cur = st.top();               // 访问右子树，而右子树已被保存在栈中
            st.pop();
        }            
        nums.push_back(cur->val);  // 访问根节点
        if (cur->right) st.push(cur->right); // 保存待遍历节点
        cur = cur->left; // 继续访问左子树
    }             
}　

　　前序遍历 3)：

void preorderTraversal(TreeNode* root, vector<int>& nums) {
　　stack<TreeNode* > st; 
    if (!root)
        return;
    st.push(root);

    while (!st.empty()) {
        TreeNode* cur = st.top();
        st.pop();
        nums.push_back(cur->val);
        if (cur->right)
            st.push(cur->right);
        if (cur->left)
            st.push(cur->left); 
    }             
}

　　中序遍历：

void inorderTraversal(TreeNode* root, vector<int>& nums) {
    TreeNode* cur = root;
    stack<TreeNode* > st; 

    while (cur || !st.empty()) {
        if (cur) {                                 // 找到最左节点并保存根节点
            st.push(cur);                     // 即访问左子树
            cur = cur->left;
        } else {                                  
            cur = st.top();
            st.pop();
            nums.push_back(cur->val);    // 访问根节点
            cur = cur->right;                      // 访问右子树
        }
    }
} 

　　后序遍历 1) 遍历结果需要翻转：

void postorderTraversal(TreeNode* root, vector<int>& nums) {
    stack<TreeNode* > st;
    TreeNode* cur = root;

    while (cur || !st.empty()) {
        if (cur) {
            nums.push_back(cur->val);
            st.push(cur);
            cur = cur->right;
        } else {
            cur = st.top();
            st.pop();
            cur = cur->left;
        }
    }
    reverse(nums.begin(), nums.end());
}

　　后序遍历 2) 遍历结果需要翻转：

void postorderTraversal(TreeNode* root, vector<int>& nums) {
    stack<TreeNode* > st;
    TreeNode* cur = root;

    while (cur|| !st.empty()) {
        if (!cur) {
            cur= st.top();
            st.pop();
        }
        nums.push_back(cur->val);
        if (cur->left) st.push(cur->left);
        cur= cur->right;
    }
    reverse(nums.begin(), nums.end());
}

　　后序遍历 3) 遍历结果无需翻转：

void postorderTraversal(TreeNode* root, vector<int>& nums) {
    stack<TreeNode* > st;
    TreeNode* cur = root, *pre = nullptr;

    while (cur || !st.empty()) {
        while (cur) {          // 找到最左节点，并存储沿路节点
            st.push(cur);
            cur = cur->left;
        }
        cur = st.top();        // 
        if (!cur->right || cur->right == pre) {  // 右子树已遍历或为空，则访问根节点
            nums.push_back(cur->val);           // 并将根节点从栈中推出
            pre = cur;
            st.pop();
            cur = nullptr;        // cur置为null，从而再从栈中取节点，即返回父节点
        } else {                                 
            cur = cur->right;     // 当前节点的右子树尚未遍历，则该节点保留在栈中
        }                         // 遍历右子树
    }
}

 3.Morris遍历

　　Morris算法基于线段树，利用叶子结点的空指针建立索引，此索引按照中序遍历的顺序建立。

　　前序遍历：

　　

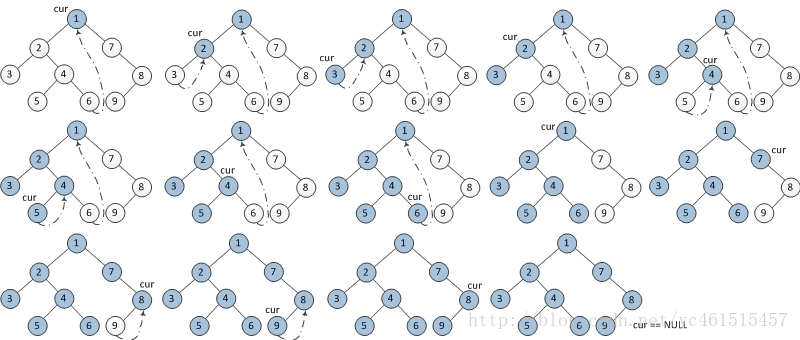
void preorderTraversal(TreeNode* root, vector<int>& nums) {
    TreeNode* cur = root, *pre = nullptr;

    while (cur) {
        if (cur->left) {   // 左孩子不为空，则找中序遍历下的前驱结点
            pre= cur->left;  // 前驱结点为左子树的最右节点
            while (pre->right && pre->right != cur) { // 找到最优节点，且该节点未建立线索
                pre = pre->right; // cur的中序遍历下的前驱结点
            }

            if (pre->right == cur) {  // cur与pre已建立线索，则去掉该线索
                pre->right = nullptr;  // 剪掉线索
                cur= cur->right;       // 左子树已遍历完毕，遍历右子树
            } else {                    // cur与pre并未建立线索，则建立线索
                nums.push_back(cur->val);
                pre->right = cur;   
                cur= cur->left;    // 遍历左子树，继续建立线索
            }
        } else {
            nums.push_back(cur->val);   
            cur = cur->right;  // 左子树为空，则返回父节点，且父节点已与此节点已建立线索，即parent = cur->right
        }
    }
}

　　中序遍历：

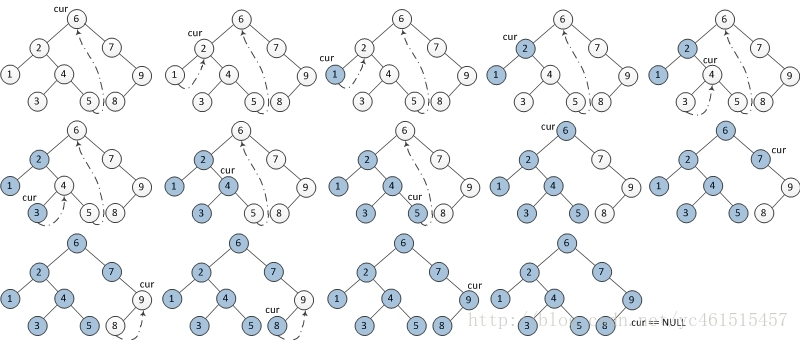
void inorderTraversal(TreeNode* root, vector<int>& nums) {
    TreeNode* cur = root, *pre = nullptr;

    while (cur) {
        if (cur->left) {
            pre = cur->left;
            while (pre->right && pre->right != cur) {
                pre = pre->right;
            }

            if (pre->right == cur) {
                nums.push_back(cur->val); // 建立的线索是根据中序遍历
                pre->right = nullptr;
                cur = cur->right;
            } else {
                pre->right = cur;
                cur = cur->left;
            }               
        } else {
            nums.push_back(cur->val);
            cur = cur->right;
        }
    }
} 

　　后序遍历：

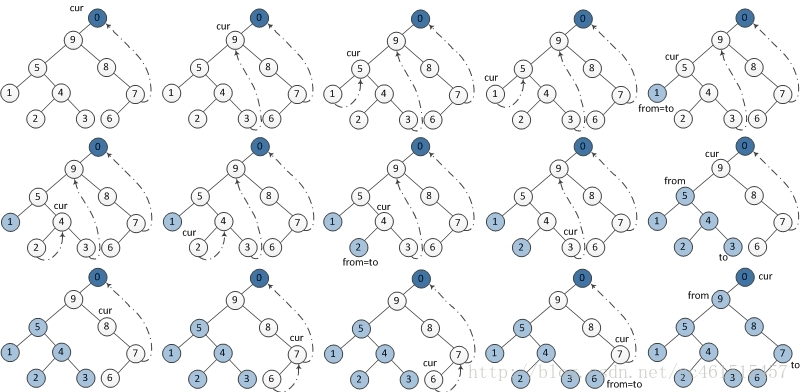
void postorderTraversal(TreeNode* root, vector<int>& nums) {
    TreeNode* cur = root, *pre = nullptr;

    while (cur) {
        if (cur->right) {
            pre = cur->right;
            while (pre->left && pre->left != cur) {
                pre = pre->left;
            }

            if (pre->left == cur) {
                pre->left = nullptr;
                cur = cur->left;
            } else {
                nums.push_back(cur->val);
                pre->left = cur;
                cur = cur->right;
            }

        } else {
            nums.push_back(cur->val);
            cur = cur->left;
        }
    }
    reverse(nums.begin(), nums.end());
} 

4.分治

　　前序遍历：

vector<int> preorderTraversal(TreeNode* root) {
    vector<int> res;
    if (!root)
        return res;
        
    vector<int> leftSubTree = preorderTraversal(root->left);
    vector<int> rightSubTree = preorderTraversal(root->right);

    res.push_back(root->val);
    res.insert(res.end(), leftSubTree.begin(), leftSubTree.end());
    res.insert(res.end(), rightSubTree.begin(), rightSubTree.end());

    return res;       
}