【洛谷】训练场_简单数学篇（不全）

P1865 A%B Problem

题意：

求区间质数的个数。

分析：

简单的质数打表模板题，根据题目再添加一点限制条件即可AC。

因为m最大才1e6，所以打表是可以的。

简单说说打表的思路：（埃式筛法）

从最小的质数2开始，将表中所有2的倍数都划去，然后再到质数3，将表中所有3的倍数都划去......以此类推。

0，1先特殊处理一下。

// 参考《挑战程序设计竞赛》P119
bool is_prime[1000005];
int prime[1000005];

// O(nloglogn)
void prime_table(){ // 这里的范围定义为 1e6
    is_prime[0] = is_prime[1] = false; // 特殊处理 0，1
    for(int i = 2; i <= 1000000; i++) is_prime[i] = true;
    for(int i = 2; i <= 1000000; i++){
        if(is_prime[i]){
            // 把 质数i 的倍数从表里划去
            for(int j = i+i; j <= 1000000; j+=i) is_prime[j] = false; 
        }
    }
}

#include<iostream>
#include<cstdio>
using namespace std;

int n, m;
bool is_prime[1000005];

void sieve(){
    for(int i = 0; i <= 1000000; i++) is_prime[i] = true;
    is_prime[0] = is_prime[1] = false;
    for(int i = 2; i <= 1000000; i++){
        if(is_prime[i]){
//            prime[p++] = i;
            for(int j = 2 * i; j <= 1000000; j+=i) is_prime[j] = false;
        }
    }
}

int main()
{
    sieve();
    while(cin >> n >> m){
        int l, r, ans;
        for(int a = 0; a < n; a++){
            cin >> l >> r;
            ans = 0;
            if(l > m || r > m || l <= 0 || r <= 0){
                cout << "Crossing the line
";
            }
            else{
                for(int i = l; i <= r; i++){
                    if(is_prime[i]) ans++;
                }
                cout << ans << endl;
            }
        }
    }
    return 0;
}

下一题：

P1372 又是毕业季Ⅰ

题意：

在n个数中（每个数的大小以次是1~n）中，找到k个数中的最大公约数。

分析：

（请拿出笔和纸来一起列下式子分析下，如果是数学大牛的话，请忽略这段话）

（感谢kkkse03的题解）

在n个数里，每个数的大小是1，2，3，...，n-1，n；

所取的k个数分别是X1，X2，X3，...，Xk-1, Xk；

设最大公约数为a，

则有 X1 >= 1a， X2 >= 2a，...，Xk >= ka ①；

同时又因为 Xk <= n ②

又①②得 ka <= n，转换一下就是 a <= [n/k] （[]为取整符号）

另外，取[n/k]，2*[n/k]，3*[n/k]，...，k*[n/k]，满足最大公约数a = [n/k]，且都小于等于n大于等于1，且互不相等，满足条件。

（如果觉得还不清楚请看洛谷题解吧dbq）

因此这就被当作是入门难度的题目处理了（代码确实很短）

#include<iostream>
using namespace std;

int main()
{
    int n, k;
    while(cin >> n >> k){
        cout << n / k << endl;
    }
    return 0;
}

也是一道辗转相除法的题目，运用了辗转相除法的思想：

公约数a， y = ax + b （y >= ax）

这样的思维才得出了以上关系式。

下一题：

P1582倒水

题意：

一天，CC买了N个容量可以认为是无限大的瓶子，开始时每个瓶子里有1升水。接着~~CC发现瓶子实在太多了，于是他决定保留不超过K个瓶子。每次他选择两个当前含水量相同的瓶子，把一个瓶子的水全部倒进另一个里，然后把空瓶丢弃。(不能丢弃有水的瓶子)

显然在某些情况下CC无法达到目标，比如N=3,K=1。此时CC会重新买一些新的瓶子(新瓶子容量无限，开始时有1升水)，以到达目标。

现在CC想知道，最少需要买多少新瓶子才能达到目标呢？

分析：

相同容量时的瓶子才能合二为一→二叉树状图→2的次方！

要最少的瓶子就是2的次方数相加的和比N大的最小值。

N不是2的次方数的情况：

留k瓶水，则要找k个2的次方数，

当k!=1时，找比k/2大的2的次方数，然后N减去这个2的次方数；

当k==1时，找比k大的2的次方数；

N是2的次方数的情况：

只要确认下N是不是2的次方数即可输出0；

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;

long long n, k;

int main()
{
    while(cin >> n >> k){
        long long num, ans;
        while(k>0 && n > 0){
            num = 1;
            if(k == 1){
                while(num < n){
                    num *= 2;
                    if(num == n) ans = 0;
//                    printf("k:%lld n:%lld num:%lld
", k, n, num);

                }
                ans = num - n;
//                printf("k:%d n:%d num:%d
", k, n, num);
            }
            else {
                while(num <= n / 2){
                    num *= 2;
                }
//                printf("k:%d n:%d num:%d
", k, n, num);
                n -= num;
                ans = n;
            }
            k--;
        }
        cout << ans << endl;
    }
    return 0;
}

下一题：

P2158[SDOI2008]仪仗队

题意：

分析：

题目很好懂，但怎么想都觉得很麻烦，因为N<=40000，不能开二维数组。

（作者unsigned说这是一道欧拉函数题，tql）

对unsigned的题解上的补充。

欧拉函数(Eular(int n))的效果是输出比n小与n互质的个数。

公式是：

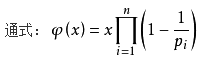
右式= x(1-1/p1)(i-1/p2)*...*(1-1/pn)；

为了防止爆数可以这样处理：

右式=x*p1(p1-1)*p2(p2-1)*...*pn(pn-1)；

int eular(int n)
{
    int ret=1,i;
    for(i=2;i*i<=n;i++) // 运用 筛法, 找 n 的因数
    {
        if(n%i==0)  // i 是 n 的因数, 且是质数
        {
            n/=i,ret*=i-1;
            while(n%i==0) n/=i,ret*=i;
        }
    }
    if(n>1) ret*=n-1; // n 本身变成了质数或者本来就是质数
    return ret;
}

void phi_table()
{
    phi[0] = 0, phi[1] = 1; // 1的欧拉函数值为1, 唯一与1互质的数
    for(int i = 2; i < maxn; i++) phi[i] = i; // 先初始化为其本身
    for(int i = 2; i < maxn; i++){
        if(phi[i] == i){ // 如果欧拉函数值仍为其本身, 说明i为素数
            for(int j = i; j < maxn; j += i)// 把i的欧拉函数值改变, 同时也把能被素因子i整除的数的欧拉函数值改变
            phi[j] = phi[j] / i * (i - 1);
        }
    }
}

// 感谢 unsigned作者 精彩的分析
#include<cstdio>
#include<iostream>
using namespace std;

int n;
int prime[40002];

void phi_table(){
    for(int i = 0; i <= 40000; i++) prime[i] = i;
    for(int i = 2; i <= 40000; i++){
        if(prime[i] == i){
            for(int j = i; j <= 40000; j += i)
            prime[j] = prime[j] / i * (i - 1);
        }
    }
}

int main()
{
    phi_table();
    while(cin >> n){
        if(n == 1) { cout << 0 << endl; continue; }
        else{
            int ans = 2;
            for(int i = 2; i < n; i++) ans += prime[i] * 2;
            cout << ans + 1 << endl;
        }
    }
    return 0;
}

今天收获：

复习了与gcd，质数，欧拉函数有关的数学题，数学题要多写，找规律。

（数学不太好的我太吃亏了）