In order to put away old things and welcome a fresh new year, a thorough cleaning of the house is a must.
Little Tommy finds an old polynomial and cleaned it up by taking it modulo another. But now he regrets doing this...
Given two integers p and k, find a polynomial f(x) with non-negative integer coefficients strictly less than k, whose remainder is p when divided by (x + k). That is, f(x) = q(x)·(x + k) + p, where q(x) is a polynomial (not necessarily with integer coefficients).
The only line of input contains two space-separated integers p and k (1 ≤ p ≤ 1018, 2 ≤ k ≤ 2 000).
If the polynomial does not exist, print a single integer -1, or output two lines otherwise.
In the first line print a non-negative integer d — the number of coefficients in the polynomial.
In the second line print d space-separated integers a0, a1, ..., ad - 1, describing a polynomial 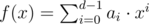 fulfilling the given requirements. Your output should satisfy 0 ≤ ai < k for all 0 ≤ i ≤ d - 1, and ad - 1 ≠ 0.
fulfilling the given requirements. Your output should satisfy 0 ≤ ai < k for all 0 ≤ i ≤ d - 1, and ad - 1 ≠ 0.
If there are many possible solutions, print any of them.
46 2
7
0 1 0 0 1 1 1
2018 214
3
92 205 1
In the first example, f(x) = x6 + x5 + x4 + x = (x5 - x4 + 3x3 - 6x2 + 12x - 23)·(x + 2) + 46.
In the second example, f(x) = x2 + 205x + 92 = (x - 9)·(x + 214) + 2018.
思路:f(x) = g(x)(x + k) + p, 设g(x) = f1(x)x + p1, 则f(x) = (f1(x)(x + k) + p1)x + kp1 + p.现在我们要使0 <= kp1 + p < k,故可唯一确定一个p1,进而转化为对g(x) = f1(x)(x+ k) + p1
问题的求解,因为g(x)的常数项即为f(x)的一次项系数,这样我们一直运算到当前0 <= p < k为止。可以证明,随着子问题的深入,p是向[0, k)靠拢的,因此这个问题有唯一解。
#include <iostream> #include <fstream> #include <sstream> #include <cstdlib> #include <cstdio> #include <cmath> #include <string> #include <cstring> #include <algorithm> #include <queue> #include <stack> #include <vector> #include <set> #include <map> #include <list> #include <iomanip> #include <cctype> #include <cassert> #include <bitset> #include <ctime> using namespace std; #define pau system("pause") #define ll long long #define pii pair<int, int> #define pb push_back #define mp make_pair #define clr(a, x) memset(a, x, sizeof(a)) const double pi = acos(-1.0); const int INF = 0x3f3f3f3f; const int MOD = 1e9 + 7; const double EPS = 1e-9; ll p, k; stack<ll> ans; void solve(ll p) { if (0 <= p && p < k) { ans.push(p); return; } ll tp; if (p > 0) { tp = -(p / k); } else { tp = (-p + k - 1) / k; } solve(tp); ans.push(tp * k + p); } int main() { scanf("%lld%lld", &p, &k); solve(p); printf("%d ", ans.size()); while (ans.size()) { ll x = ans.top(); ans.pop(); printf("%lld ", x); } return 0; }