The war is about to start between Demacia and Noxus. Noxus's army has n soldiers. Noxus's soldiers are stronger than Demacia's soldiers, so Demacia's soldiers can win only if their number is larger than the number of Noxus's soldiers.
Lux is a magical girl from Demacia, she decided to help her city's army! Lux can shoot an infinite laser in a straight line with a width equal to z and can kill all the enemies in the path! Lux can send the laser only one time, so she needs to kill at least m soldiers to help Demacia's soldiers win the fight.
Lux stands at the point (0, 0) and she knows the positions of every soldier from Noxus, she wants to know if she can help Demacia's army to win the war. Can you help her?
The first line contains an integer T (1 ≤ T ≤ 100) specifying the number of test cases.
The first line of each test case contains two integers n and m, and a floating point number z (1 ≤ n, m ≤ 1000, 0 < z ≤ 30000), in which nis the number of soldiers in Noxus's army, m is the minimum number of soldiers Lux must kill, and z is the width of Lux's laser.
Then n lines follow describe each Noxus's Soldier, in which the ith line contains 2 integers xi, yi ( - 104 ≤ xi, yi ≤ 104), representing the coordinates of the ith soldier.
It is guaranteed that no two soldiers share the same pair of coordinates, neither with Lux's position.
For each test case, print a single line containing "Yes" (without quotes) if Demacia's army can win. Otherwise, print "No" (without quotes).
1
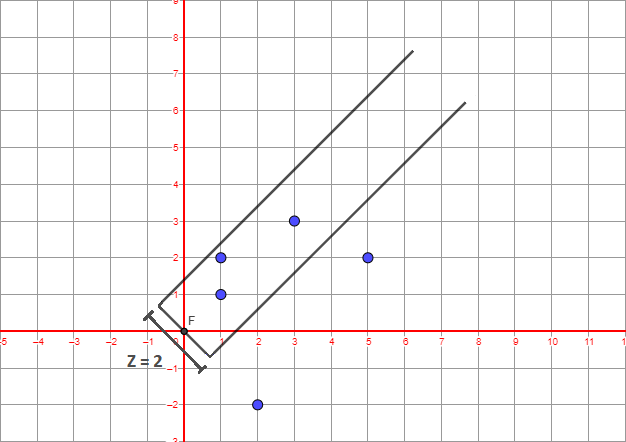
5 3 2
1 1
1 2
2 -2
3 3
5 2
Yes
思路:对每个点考虑什么角度范围能覆盖到他,然后就变成了求一个点被最多的区间覆盖问题,离散化后差分求最大前缀和即可。复杂度nlogn.

1 #include <iostream> 2 #include <fstream> 3 #include <sstream> 4 #include <cstdlib> 5 #include <cstdio> 6 #include <cmath> 7 #include <string> 8 #include <cstring> 9 #include <algorithm> 10 #include <queue> 11 #include <stack> 12 #include <vector> 13 #include <set> 14 #include <map> 15 #include <list> 16 #include <iomanip> 17 #include <cctype> 18 #include <cassert> 19 #include <bitset> 20 #include <ctime> 21 22 using namespace std; 23 24 #define pau system("pause") 25 #define ll long long 26 #define pii pair<int, int> 27 #define pb push_back 28 #define mp make_pair 29 #define clr(a, x) memset(a, x, sizeof(a)) 30 31 const double pi = acos(-1.0); 32 const int INF = 0x3f3f3f3f; 33 const int MOD = 1e9 + 7; 34 const double EPS = 1e-11; 35 36 /* 37 #include <ext/pb_ds/assoc_container.hpp> 38 #include <ext/pb_ds/tree_policy.hpp> 39 40 using namespace __gnu_pbds; 41 tree<pli, null_type, greater<pli>, rb_tree_tag, tree_order_statistics_node_update> T; 42 */ 43 44 int T, n, m; 45 double z; 46 struct Double { 47 double val; 48 Double () {} 49 Double (double val) : val(val) {} 50 bool operator < (const Double &D) const { 51 return val < D.val - EPS; 52 } 53 }; 54 struct seg { 55 Double x, y; 56 seg () {} 57 seg (Double x, Double y) : x(x), y(y) {} 58 } s[2015]; 59 map<Double, int> mmp; 60 int cnt[2015]; 61 int main() { 62 scanf("%d", &T); 63 while (T--) { 64 mmp.clear(); 65 clr(cnt, 0); 66 int cnt_s = 0; 67 mmp[Double(-pi)], mmp[Double(pi)]; 68 scanf("%d%d%lf", &n, &m, &z); 69 for (int i = 1; i <= n; ++i) { 70 int x, y; 71 scanf("%d%d", &x, &y); 72 if (z * z < 4 * (x * x + y * y)) { 73 double th1 = atan2(y, x); 74 double th2 = asin(z / 2.0 / sqrt(x * x + y * y)); 75 double t1 = th1 - th2, t2 = th1 + th2; 76 if (t1 < -pi) { 77 s[++cnt_s] = seg(Double(t1 + 2 * pi), Double(pi)); 78 s[++cnt_s] = seg(Double(-pi), Double(t2)); 79 t1 += 2 * pi; 80 } else if (t2 > pi) { 81 s[++cnt_s] = seg(Double(t1), Double(pi)); 82 s[++cnt_s] = seg(Double(-pi), Double(t2 - 2 * pi)); 83 t2 -= 2 * pi; 84 } else { 85 s[++cnt_s] = seg(Double(t1), Double(t2)); 86 } 87 mmp[Double(t1)], mmp[Double(t2)]; 88 } else { 89 double th = atan2(y, x); 90 double t1 = th - pi / 2, t2 = th + pi / 2; 91 if (t1 < -pi) { 92 s[++cnt_s] = seg(Double(t1 + 2 * pi), Double(pi)); 93 s[++cnt_s] = seg(Double(-pi), Double(t2)); 94 t1 += 2 * pi; 95 } else if (t2 > pi) { 96 s[++cnt_s] = seg(Double(t1), Double(pi)); 97 s[++cnt_s] = seg(Double(-pi), Double(t2 - 2 * pi)); 98 t2 -= 2 * pi; 99 } else { 100 s[++cnt_s] = seg(Double(t1), Double(t2)); 101 } 102 mmp[Double(t1)], mmp[Double(t2)]; 103 } 104 } 105 int cnt_index = 0; 106 for (map<Double, int>::iterator it = mmp.begin(); it != mmp.end(); ++it) { 107 it -> second = ++cnt_index; 108 //printf("%.12f ", it -> first.val); 109 } 110 for (int i = 1; i <= cnt_s; ++i) { 111 ++cnt[mmp[s[i].x]], --cnt[mmp[s[i].y] + 1]; 112 } 113 int ans = 0; 114 for (int i = 1; i <= cnt_index + 1; ++i) { 115 cnt[i] += cnt[i - 1]; 116 ans = max(ans, cnt[i]); 117 } 118 //printf("%d ", ans); 119 puts(ans >= m ? "Yes" : "No"); 120 } 121 return 0; 122 }
