石子游戏
Time Limit: 10 Sec Memory Limit: 256 MBDescription

Input

Output
输出T行,表示每组的答案。
Sample Input
3
1
1
2
1
0 0
3
1 2 2
4 4 4 4
Sample Output
1
0
6
0
6
HINT
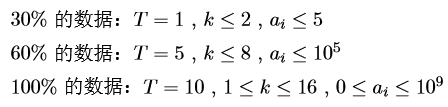
Solution
这显然是一道博弈论的题目。我们发现这是一个树结构,仔细看了一下,发现这显然是一个阶梯Nim的模型。
我们将所有和同n奇偶的值XOR起来就可以得到SG。我们先判断一下,若SG=0则显然必败,否则必胜。
然后我们开始计算方案,枚举每一个节点,目标显然就是要让SG=0。
由于XOR的消去率,根据题意,可以分 2 种情况分别讨论:(根据SG异或值判断是加入还是取出。)
1. 从父亲那加入值,显然就是需要 ( SG^a[这个点] ) - a[这个点的父亲] <= a[这个点],这样才可以通过加入若干个值使得SG=0;
2. 把值给儿子,显然需要 (SG^a[这个点]) <= a[这个点],这样才可以通过拿走若干的值使得SG=0。
然后我们讨论一下是否为叶子节点:
1. 非叶节点,若从父亲那加入值只有1的贡献,把值给儿子(由于有两个儿子)所以贡献为2;
2. 叶子节点,从父亲那加入值或者彻底删去都显然只有1的贡献。
这样就可以求出方案数了。
Code

1 #include<iostream>
2 #include<algorithm>
3 #include<cstdio>
4 #include<cstring>
5 #include<cstdlib>
6 #include<cmath>
7 using namespace std;
8
9 const int ONE = 10001;
10 const int INF = 214783640;
11 const int MOD = 1e9+7;
12
13 int T;
14 int n;
15 int x,num;
16 int a[17][65537];
17 int SG,Ans;
18
19 int get()
20 {
21 int res=1,Q=1; char c;
22 while( (c=getchar())<48 || c>57)
23 if(c=='-')Q=-1;
24 if(Q) res=c-48;
25 while((c=getchar())>=48 && c<=57)
26 res=res*10+c-48;
27 return res*Q;
28 }
29
30 void Solve()
31 {
32 n=get();
33 SG=Ans=0;
34 for(int i=1;i<=n;i++)
35 for(int j=1;j<=(1<<(i-1));j++)
36 {
37 a[i][j]=get();
38 if(i%2==n%2) SG ^= a[i][j];
39 }
40 if(!SG) {printf("0"); return;}
41
42 for(int i=1;i<=n;i++)
43 {
44 for(int j=1;j<=(1<<(i-1));j++)
45 if(i%2==n%2)
46 {
47 if(i!=n)
48 {
49 if( (SG^a[i][j]) <= a[i][j]) Ans+=2;
50 if( (SG^a[i][j]) > a[i][j] && (SG^a[i][j]) - a[i-1][(j-1)/2+1] <= a[i][j]) Ans+=1;
51 }
52 if(i==n)
53 {
54 if( (SG^a[i][j]) <= a[i][j] ) Ans++;
55 if( (SG^a[i][j]) > a[i][j] && (SG^a[i][j]) - a[i-1][(j-1)/2+1] <= a[i][j] ) Ans++;
56 }
57 }
58 }
59
60 printf("%d",Ans);
61 }
62
63 int main()
64 {
65 T=get();
66 while(T--)
67 Solve(),printf("
");
68 }
