【BZOJ2440】完全平方数 [莫比乌斯函数]

完全平方数

Time Limit: 10 Sec  Memory Limit: 128 MB
[Submit][Status][Discuss]

Description

　　小X自幼就很喜欢数。
　　但奇怪的是，他十分讨厌完全平方数。
　　他觉得这些数看起来很令人难受。
　　由此，他也讨厌所有是完全平方数的正整数倍的数。
　　然而这丝毫不影响他对其他数的热爱。
　　这天是小X的生日，小 W 想送一个数给他作为生日礼物。
　　当然他不能送一个小X讨厌的数。他列出了所有小X不讨厌的数，然后选取了第 K个数送给了小X。
　　小X很开心地收下了。
　　然而现在小 W 却记不起送给小X的是哪个数了。
　　你能帮他一下吗？

Input

　　包含多组测试数据。文件第一行有一个整数 T，表示测试数据的组数。
　　第 2 至第 T+1 行每行有一个整数 Ki，描述一组数据，含义如题目中所描述。 

Output

　　含 T 行，分别对每组数据作出回答。第 i 行输出相应的
　　第 Ki 个不是完全平方数的正整数倍的数。

Sample Input

　　4
　　1
　　13
　　100
　　1234567

Sample Output

　　1
　　19
　　163
　　2030745

HINT

　　对于 100% 的数据有 1 ≤ Ki ≤ 10^9, T ≤ 50

Main idea

　　询问第 k 个不含完全平方因子的数。

Source　　

　　显然我们可以简化一下问题，二分答案。那么我们就只需要知道：1~n中 不含完全平方因子 的数的个数。

　　然后我们思考一下容斥，用(总数-完全平方数个数)：完全平方数个数 = 至少有1个质数平方因子的数 - 至少2个质数平方因子的数 + 至少3个质数平方因子的数……
　　（假设你有一堆质数 {P_1, ..., P_n}，A_i 表示的是 包含 P_i^2 作为因子的数的集合）　　

　　也就是：奇数个质数平方因子的数 - 偶数个质数平方因子的数。
　　然后我们发现，那么可以枚举一个d，删除d^2相关，这时候系数也就是μ(d)，求一下莫比乌斯函数即可。当d有奇数个质数因子的时候，删除的是有奇数个质数平方因子中d^2的倍数。
　　整理成式子也就是：

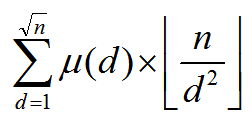
Code

#include<iostream>  
#include<string>  
#include<algorithm>  
#include<cstdio>  
#include<cstring>  
#include<cstdlib>  
#include<cmath>
using namespace std; 
typedef long long s64;
 
const int ONE = 44725;
   
int T;
int n,m;
int prime[ONE],miu[ONE],isp[ONE],p_num;
 
int get() 
{
        int res=1,Q=1;  char c;
        while( (c=getchar())<48 || c>57)
        if(c=='-')Q=-1;
        if(Q) res=c-48; 
        while((c=getchar())>=48 && c<=57) 
        res=res*10+c-48; 
        return res*Q; 
}
 
void Getmiu(int MaxN)
{
        miu[1] = 1;
        for(int i=2; i<=MaxN; i++)
        {
            if(!isp[i])
                isp[i] = 1, prime[++p_num] = i, miu[i] = -1;
            for(int j=1; j<=p_num, i*prime[j]<=MaxN; j++)
            {
                isp[i * prime[j]] = 1;
                if(i % prime[j] == 0)
                {
                    miu[i * prime[j]] = 0;
                    break;
                }
                miu[i * prime[j]] = -miu[i];
            }
        }
}
 
s64 Check(s64 n)
{
        s64 res = 0 ,Q = sqrt(n);
        for(int d=1; d<=Q; d++)
            res += miu[d] * (n/(d*d));
        return res;
}
 
void Solve()
{
        n = get();
        s64 l = 0, r = 2e9;
        while( l < r-1 )
        {
            s64 mid = (l+r)>>1;
            if(Check(mid) < n) l = mid;
            else r = mid;
        }
         
        if(Check(r) <= n) printf("%d", r);
        else printf("%d", l); 
        printf("
");
}
 
int main()
{
        Getmiu(ONE-1);
        T = get();
        while(T--)
            Solve();
}