小Y的地铁
Time Limit: 50 Sec Memory Limit: 256 MBDescription
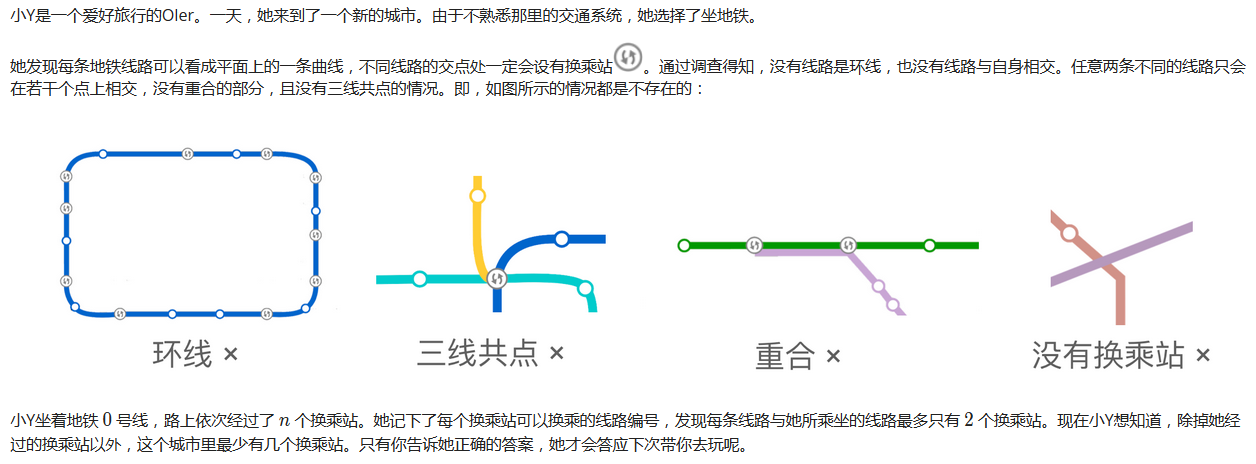
Input

Output
对于每组输入数据,输出一行一个整数,表示除掉这 n 个换乘站之外,最少有几个换乘站。
Sample Input
4
4
1 2 1 2
8
1 2 3 4 1 2 3 4
5
5 4 3 3 5
8
1 2 3 4 1 3 2 4
Sample Output
0
0
0
1
HINT
n <= 44
Solution
首先,答案显然只和几个区域的连通状态有关,那么我们可以写出四种本质不同的方案。(即下图中被线分开的六块)。
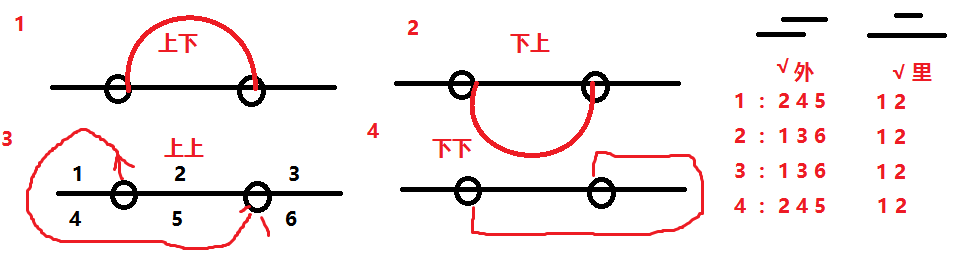
我们可以考虑,对于一条线,其他线(显然仅有 部分相交 与 完全相交 两种)造成的贡献。打出表来,上图是不会造成交点的线段种类。
既然知道了这个,我们的复杂度显然可以做到 O(4 ^ (n / 2))。还是不足以通过,怎么办呢?
模拟退火大法好!
Code

1 #include<iostream> 2 #include<string> 3 #include<algorithm> 4 #include<cstdio> 5 #include<cstring> 6 #include<cstdlib> 7 #include<cmath> 8 #include<ctime> 9 using namespace std; 10 typedef long long s64; 11 12 const int ONE = 105; 13 const int INF = 2147483640; 14 15 int get() 16 { 17 int res = 1, Q = 1; char c; 18 while( (c = getchar()) < 48 || c > 57) 19 if(c == '-') Q = -1; 20 if(Q) res = c - 48; 21 while( (c = getchar()) >= 48 && c <= 57) 22 res = res * 10 + c - 48; 23 return res * Q; 24 } 25 26 int n, num; 27 int pos[ONE], val[ONE]; 28 int vis[ONE], a[ONE]; 29 int Ans = INF; 30 struct power {int l, r;} A[ONE]; 31 32 int x[ONE][ONE], y[ONE][ONE]; 33 34 void Deal_first() 35 { 36 x[1][2] = x[1][4] = x[1][5] = 1; 37 x[2][1] = x[2][3] = x[2][6] = 1; 38 x[3][1] = x[3][3] = x[3][6] = 1; 39 x[4][2] = x[4][4] = x[4][5] = 1; 40 for(int i = 1; i <= 4; i++) y[i][1] = y[i][2] = 1; 41 } 42 43 int Now; 44 45 int Judge(int pos, int type) 46 { 47 int res = Now; 48 for(int i = pos, j = pos + 1; j <= num; j++) 49 { 50 if(A[i].r < A[j].l) continue; 51 if(A[i].r < A[j].r) res -= !x[a[i]][a[j]]; 52 if(A[j].r < A[i].r) res -= !y[a[i]][a[j]]; 53 } 54 for(int i = 1, j = pos; i < pos; i++) 55 { 56 if(A[i].r < A[j].l) continue; 57 if(A[i].r < A[j].r) res -= !x[a[i]][a[j]]; 58 if(A[j].r < A[i].r) res -= !y[a[i]][a[j]]; 59 } 60 61 a[pos] = type; 62 63 for(int i = pos, j = pos + 1; j <= num; j++) 64 { 65 if(A[i].r < A[j].l) continue; 66 if(A[i].r < A[j].r) res += !x[a[i]][a[j]]; 67 if(A[j].r < A[i].r) res += !y[a[i]][a[j]]; 68 } 69 for(int i = 1, j = pos; i < pos; i++) 70 { 71 if(A[i].r < A[j].l) continue; 72 if(A[i].r < A[j].r) res += !x[a[i]][a[j]]; 73 if(A[j].r < A[i].r) res += !y[a[i]][a[j]]; 74 } 75 76 Now = res, Ans = min(Ans, res); 77 return res; 78 } 79 80 double Random() {return (double)rand() / RAND_MAX;} 81 void SA() 82 { 83 if(num == 0) return; 84 double T = num * 2; 85 while(T >= 0.01) 86 { 87 int pos = rand() % num + 1, type = rand() % 4 + 1; 88 int ori = Now, ori_type = a[pos]; 89 90 int dE = Judge(pos, type) - ori; 91 if(dE <= 0 || Random() <= exp(-dE / T)) a[pos] = type; 92 else Judge(pos, ori_type); 93 94 T *= 0.9993; 95 } 96 } 97 98 void Deal() 99 { 100 Ans = INF; 101 n = get(); 102 for(int i = 1; i <= n; i++) a[i] = get(), pos[a[i]] = vis[a[i]] = 0; 103 for(int i = n; i >= 1; i--) 104 if(!pos[a[i]]) pos[a[i]] = i; 105 106 num = 0; 107 for(int i = 1; i <= n; i++) 108 if(!vis[a[i]] && pos[a[i]] != i) 109 A[++num] = (power){i, pos[a[i]]}, vis[a[i]] = 1; 110 111 for(int i = 1; i <= num; i++) 112 a[i] = rand() % 4 + 1; 113 Ans = 0; 114 for(int i = 1; i <= num; i++) 115 for(int j = i + 1; j <= num; j++) 116 { 117 if(A[i].r < A[j].l) break; 118 if(A[i].r < A[j].r) Ans += !x[a[i]][a[j]]; 119 if(A[j].r < A[i].r) Ans += !y[a[i]][a[j]]; 120 } 121 Now = Ans; 122 for(int i = 1; i <= 10; i++) 123 SA(); 124 printf("%d ", Ans); 125 } 126 127 int main() 128 { 129 Deal_first(); 130 int T = get(); 131 while(T--) 132 Deal(); 133 }
