【组合恒等式】(sum_{k=0}^{r}C_m^k imes C_{n}^{r-k}=C_{m+n}^r)
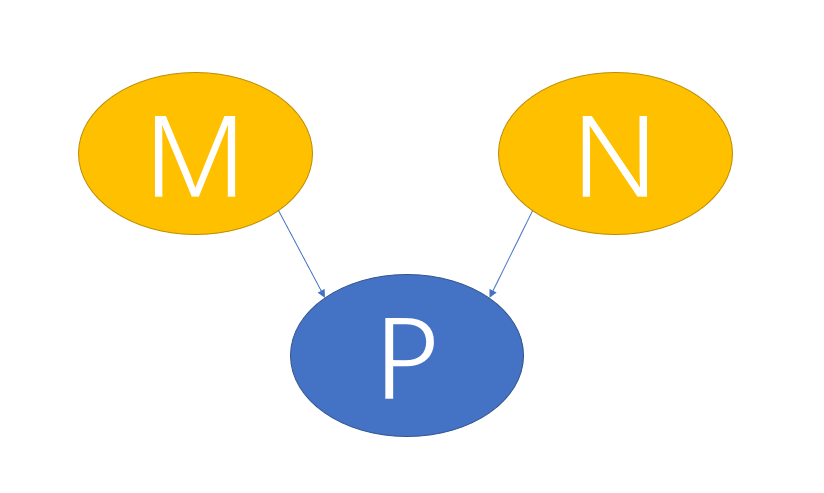
问题模型:
P舞团将从M舞团和N舞团共选拔出r个人来加入到P舞团,求问一共有多少种选法?
思路一:
在M中选x人,那么就在N中选r-x人最终只需对所有情况取个西格玛,即(sum_{k=0}^{r}C_m^{k} imes C_n^{r-k}),也可以写作(sum_{k=0}^r binom{m}{k} imes binom{n}{r-k})
思路二:
直接在M、N组成的整体中直接去选取r个人,即(C_{m+n}^{r}),也可以写作( binom{m+n}{r})
由于这两种思路都是正确的,故而由这两个式子算出来的结果是相等的。
此外,需要注意的是在运用这个公式需要注意一下是否满足(r<=min(m,n))这个前提条件。
推论
(sum_{k=0}^{r}C_m^{k} imes C_n^{r-k}=C_{m+n}^{r})
若将该公式中r替换为n,我们将有
(sum_{k=0}^{n}C_m^{k} imes C_n^{n-k}=C_{m+n}^{n})
经过化简,我们有
(sum_{k=0}^{n}C_m^{k} imes C_n^{k}=C_{m+n}^{m})
也可以写作(sum_{k=0}^{n} binom{m}{k} imes binom{n}{k} = binom{m+n}{m})