查找表，Two Sum，15. 3Sum，18. 4Sum，16 3Sum Closest，149 Max points on line

Two Sum:

解法一：排序后使用双索引对撞：O(nlogn)+O(n) = O(nlogn) , 但是返回的是排序前的指针。

解法二：查找表。将所有元素放入查找表， 之后对于每一个元素a，查找 target-a 是否存在。使用map实现，键是元素的值，键值是元素对应的索引。

不能把vector中所有的值放到查找表中，因为若有重复的值，前一个会被后一个覆盖。所以改善为把当前元素v前面的元素放到查找表中。

时间复杂度:O(n)

空间复杂度：O(n)

 注意：这道题只有唯一解。

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> record;
        for(int i=0; i<nums.size();i++){
            int complement = target - nums[i];
            if(record.find(complement) != record.end()){
                int res[2] = {i, record[complement]};  //res记录两个元素的索引
                return vector<int>(res, res+2);
            }
            record[nums[i]] = i;
        }
        throw invalid_argument("The input has no solution");
    }
};

需要考虑不同的三元组：是要求值不同还是索引不同。

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int> > res;
        if(nums.size()<=2){
            return res;
        }
        
        sort(nums.begin(), nums.end());
        size_t i = 0;
        while(i<nums.size()-2){
            int target = -nums[i];
            int l = i+1;
            int r = nums.size()-1;
            while(l<r){
                int sum = nums[l]+nums[r];
                if(sum<target)
                    l++;
                else if(sum>target)
                    r--;
                else{
                    vector<int> triplet = {nums[i], nums[l], nums[r]};
                    res.push_back(triplet);
                    //避免把重复的一组数字存入res中
                    while(l<r && nums[l] == triplet[1])
                        l++;
                    while(l<r && nums[r] == triplet[2])
                        r--;
                }
            }
            int curNum = nums[i];
            while(i<nums.size()-2 && nums[i]==curNum)
                i++;
        }
        return res;
    }
};

思路和3sum差不多，也就是多加了一层循环，即这里有两层循环，然后用一对对撞指针来计算剩下的两个数之后。

需要注意的是：int(nums.size()-3) 和 int(nums.size()-2) 一定要加 int() 因为nums.size() == 0 时，因为它是unsigned int 型 , nums.size()-2=2^32-2，循环次数就炸掉了。

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        set<vector<int>> res;
        sort(nums.begin(),nums.end());
        for(int i=0;i<int(nums.size()-3);i++){
            for(int j=i+1; j<int(nums.size()-2); j++){
                if(j>i+1 && nums[j]==nums[j-1] ) continue;
                int left = j+1, right = nums.size()-1;
                while(left<right){
                    int sum = nums[i] + nums[j] + nums[left] + nums[right];
                    if(sum==target){
                        vector<int> out{nums[i], nums[j], nums[left], nums[right]};
                        res.insert(out);
                        left++;
                        right--;
                    }
                    else if(sum < target)
                        left++;
                    else
                        right--;
                }
            }
        }
        return vector<vector<int>>(res.begin(), res.end());
    }
};

 

思路：这题要求返回最接近给定值的值，所以我们要保证档期那的三个数和给定值之间的差的绝对值最小。

1）首先定义diff来记录差的绝对值，closest保存当前最小的三个数的和；

2）数组排序，以便进行左指针和右指针的移动；

3）遍历一遍数组，再使用对撞指针的思想计算三个数的和，与diff进行比较，并把较小值保存在diff中，最后返回closest。

class Solution {
public:
    int threeSumClosest(vector<int>& nums, int target) {
        int closest = nums[0] + nums[1] + nums[2];
        int diff = abs(closest - target);
        sort(nums.begin(), nums.end());
        for(int i=0; i<nums.size()-2;i++){
            int left = i+1, right = nums.size()-1;
            while(left<right){
                int sum = nums[i] + nums[left] + nums[right];
                int newDiff = abs(sum-target);
                if(diff > newDiff){
                    diff = newDiff;
                    closest = sum;
                }
                if(sum<target) left++;
                else right--;
            }
        }
        return closest;
    }
};

 

class Solution {
public:
    //时间复杂度O(n^2)
    //空间复杂度O(n^2)
    int fourSumCount(vector<int>& A, vector<int>& B, vector<int>& C, vector<int>& D) {
        unordered_map<int,int> record;
        for(int i=0;i<C.size();i++){
            for(int j=0;j<D.size();j++)
                record[C[i]+D[j]] ++;
            }
            int res = 0;
            for(int i=0; i<A.size();i++){
                for(int j=0;j<B.size();j++){
                    if(record.find(0-A[i]-B[j]) != record.end())
                        res += record[0-A[i]-B[j]];
                }
            }
            
        return res;
    }
};

本题中都是小写字母。

class Solution {
public:
    vector<vector<string>> groupAnagrams(vector<string>& strs) {
        vector<vector<string>> res;    //返回值
        unordered_map<string, vector<string>> m;   //字符串与它的同构字符串之间的映射
        for(string str: strs){
            string t = str;
            sort(t.begin(),t.end());
            m[t].push_back(str);
        }
        for(auto a:m)
            res.push_back(a.second);
        return res;
    }
};

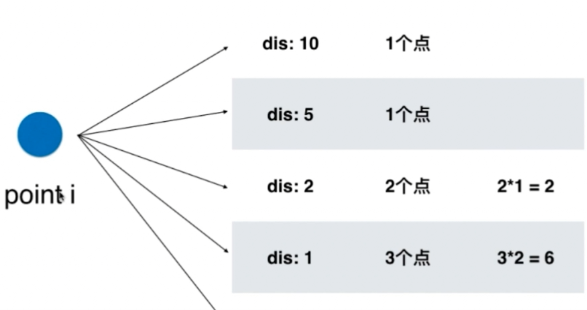
思路：如下图所示，定义一个map来记录每个点到point i 的距离，和它对应的频次。然后遍历这个map，若能找到频次大于等于2的点，则把res值累加上。

注意：为了防止距离开根号出现浮点数，这里储存距离的平凡。

//时间复杂度O(n^2)
//空间复杂度O(n)
class Solution {
public:
    int numberOfBoomerangs(vector<pair<int, int>>& points) {
        int res = 0; //记录一共有多少个符合条件的三元组
        for(int i=0; i<points.size(); i++){
            unordered_map<int, int> record;  //其余的点距离points的值，及其出现的频次
            for(int j=0;j<points.size();j++){
                if(j!=i)
                    record[ dis(points[i], points[j]) ]++;
            }
            for(unordered_map<int,int>::iterator iter=record.begin(); iter!=record.end();iter++)
                if(iter->second >=2)
                    res += (iter->second)*(iter->second-1);
        }
        return res;
    }
    
private:
    int dis(const pair<int,int> &pa, const pair<int, int> &pb){
        return (pa.first - pb.first)*(pa.first - pb.first) + 
            (pa.second-pb.second)*(pa.second-pb.second);
    }
};

 

不愧是hard模式，连代码长度都是其他题目的两倍 ==

思路：1）使用map型的lines来存储直线的斜率和对应出现的频次；

2）需要注意判断两个边界条件：两个点重合的情况和两个点的x值相同也就是斜率无限大的情况；

3）求斜率的时候使用了求两个数的最大公约数的方法，分别用这两个数来除以公约数，来得到这两个数斜率的最简值（比如4/2 和 2/1的斜率最简化的值都是2/1）。然后存储到lines中。

4）最终的result保存最大的值，注意要加上重复点的个数。

/**
 * Definition for a point.
 * struct Point {
 *     int x;
 *     int y;
 *     Point() : x(0), y(0) {}
 *     Point(int a, int b) : x(a), y(b) {}
 * };
 */
class Solution {
public:
    int maxPoints(vector<Point>& points) {
        if(points.size()<2) return points.size();
        int result = 0;
        map<pair<int, int> ,int> lines;
        for(int i=0; i<points.size();i++){
            lines.clear();
            int duplicate = 1, vertical = 1;
            for(int j=i+1;j<points.size();j++){
                if(points[j].x == points[i].x && points[j].y == points[i].y){
                    duplicate++;
                    continue;
                }
                else if(points[j].x == points[i].x) vertical++;
                else{
                    //求两点的斜率
                    int a = points[j].x - points[i].x;
                    int b = points[j].y - points[i].y;
                    int gcd = GCD(a,b);
                    a /= gcd, b /= gcd;
                    lines[make_pair(a,b)]++;   //存储对应斜率的次数
                }
            }
            if(result < duplicate) result = duplicate;
            if(result < vertical) result = vertical;
            for(auto line : lines){
                int tmp = duplicate + line.second;
                if(result < tmp) result = tmp;
            }
        }
        return result;
    }
    
private:
    int GCD(int a, int b){
        if(b==0) return a;
        else return GCD(b, a%b);
    }
};