leetcode 221

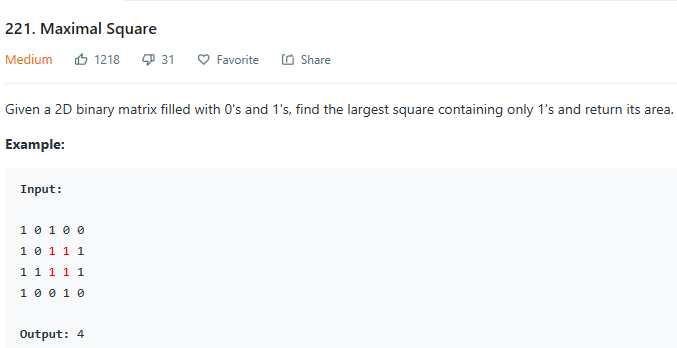
题意：给定一个0，1矩阵，找到最大的包含1的正方形，并返回它的面积。

思路：动态规划

初始化：二维数组：dp[i][j] 表示 到达（i, j ）位置所能组成的最大正方形的边长。

1）边界条件：i表示行数，j表示列数。 i == 0 || j == 0

2）状态转移方程：matrix[i][j] == 1时，dp[i][j] = min(dp[i-1][j-1], min(dp[i][j-1], dp[i-1][j] ) ) +1 

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if(matrix.empty() || matrix[0].empty()) return 0;
        
        int n = matrix.size();
        int m = matrix[0].size();
        
        int dp[n][m] = {};  //最长边长
        int res = 0; //面积
        for(int i=0; i<n; i++){
            for(int j =0;j<m; j++){
                if(i==0 || j==0)
                    dp[i][j] = matrix[i][j] - '0';
                else if(matrix[i][j] == '1'){
                    dp[i][j] = min(dp[i-1][j-1], min(dp[i-1][j], dp[i][j-1])) +1;
                }
                res = max(dp[i][j], res);
            }
        }
        return res*res;
    }
};