找出没有被X围绕的点，则剩下的就是被围绕的点，将这些O改为X。
class Solution { public: /* * @param board: board a 2D board containing 'X' and 'O' * @return: nothing */ void surroundedRegions(vector<vector<char>> &board) { // write your code here if(board.empty() || board[0].empty()) return; int n = board.size(), m = board[0].size(); vector<vector<int>> mark(n, vector<int>(m, 0)); //记录每个格子的No vector<bool> surrounded(n*m+1 , true); //记录这片区域号No是否被X环绕 int No=0; //记录一片联通的区域号 for(int i=0; i<n; i++){ for(int j=0; j<m; j++){ if(board[i][j]=='O' && mark[i][j]==0){ No++; bfs(board, mark, surrounded, No, i, j); mark[i][j] = No; } } } for(int i=0; i<n; i++){ for(int j=0; j<m; j++){ if(board[i][j] == 'O' && surrounded[mark[i][j]]) //被X环绕 board[i][j] = 'X'; } } } void bfs(vector<vector<char>> &board, vector<vector<int>>& mark, vector<bool>& surrounded, int No, int x, int y ){ int row = board.size(),col = board[0].size(); int dx[4] = {-1, 0, 1, 0}; int dy[4] = {0, -1, 0, 1}; queue<int> qx; queue<int> qy; qx.push(x); qy.push(y); //mark[x][y] = No; while(!qx.empty()){ int ox = qx.front(); int oy = qy.front(); qx.pop(); qy.pop(); if(ox == 0 || ox == row-1 || oy == 0 ||oy == col-1) //碰到边界，说明没有被X包围 surrounded[No] = false; //把这块区域No标记为false for(int i=0; i<4; i++){ int nx = ox + dx[i]; int ny = oy + dy[i]; if(nx>=0 && nx<row && ny>=0 && ny<col && mark[nx][ny]==0 && board[nx][ny]=='O'){ mark[nx][ny] = No; qx.push(nx); qy.push(ny); } } } } };
题意：
INF：空房间；-1：墙；0：门
问：从任何一个空房间到最近的门长度是多少。
不能达到的地方填INF
思路：
将所有rooms[i][j] = 0 的结点入队列，然后求BFS，判断这些门到最近的空房间的最短路径。
BFS可以用来求边长为1的图的最短路。
class Solution { public: /** * @param rooms: m x n 2D grid * @return: nothing */ static const int inf = 2147483647; int n, m; void wallsAndGates(vector<vector<int>> &rooms) { // write your code here if(rooms.empty() || rooms[0].empty()) return; n = rooms.size(), m = rooms[0].size(); int dx[4] = {-1, 0, 1, 0}; int dy[4] = {0, -1, 0, 1}; queue<int> qx; queue<int> qy; //多源点多终点最短路径：将所有的gate入队列 for(int i=0; i<n; i++){ for(int j=0; j<m; j++){ if(rooms[i][j] == 0){ qx.push(i); qy.push(j); } } } while(!qx.empty()){ int ox = qx.front(); int oy = qy.front(); qx.pop(); qy.pop(); for(int i=0; i<4; i++){ int nx = ox + dx[i]; int ny = oy + dy[i]; if(nx>=0 && nx<n && ny>=0 && ny<m && rooms[nx][ny]==inf){ qx.push(nx); qy.push(ny); rooms[nx][ny] = rooms[ox][oy] + 1; } } } } };
注意：dfs函数里的x, l, str, 不能加& 会报错：
error: invalid initialization of non-const reference of type ‘int&’ from an rvalue of type ‘int’
简单来说就是因为传入的x，l，str都是具体的数值，所以不能加&
class Solution { public: /** * @param digits: A digital string * @return: all posible letter combinations */ vector<string> ans; //当前层数x；总共层数l，中间状态str, void dfs(int x, int l, string str, string digits, vector<string>& phone){ //退出条件 if(x == l){ ans.push_back(str); return; } int num = digits[x] - '0'; for(int i=0; i<phone[num].size(); i++){ //数字num有多少种拓展情况 dfs(x+1, l, str+phone[num][i], digits, phone); } } vector<string> letterCombinations(string &digits) { // write your code here vector<string> phone = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"}; if(digits.empty()) return ans; dfs(0, digits.size(), "", digits, phone); return ans; } };
[LintCode] Factorization
A non-negative numbers can be regarded as product of its factors.
Write a function that takes an integer n and return all possible combinations of its factors.
Notice
- Elements in a combination (a1, a2, … , ak) must be in non-descending order. (ie, a1 ≤ a2 ≤ … ≤ ak).
- The solution set must not contain duplicate combination.
Example
Given n = 8
return [[2,2,2],[2,4]]
// 8 = 2 x 2 x 2 = 2 x 4.
Given n = 1
return []
Given n = 12
return [[2,6],[2,2,3],[3,4]]
By definition, factors should be greater than 1 and less than n itself, which means [1, n] is not a valid factorization of n.
To avoid duplicated fatorization answers, for a given factorization, if we've already found some factors, all factors that are
yet to be found must be >= its previously found factor.
Output condition: when n becomes 1 after dividing all the factors, we should add the current list as one of the factorization.
However, we also need to avoid adding the factorization of [n, 1]. Since we start the dfs from 2, we know that if the case of
using n itself as a factor, there should be only 1 element in the current list. Thus, when n == 1, we check if the list size is > 1.
If it is, we have a valid factorization.
// pch.cpp: 与预编译标头对应的源文件；编译成功所必需的 #include "pch.h" // 一般情况下，忽略此文件，但如果你使用的是预编译标头，请保留它。 #include <vector> #include <list> #include <map> #include <set> #include <queue> #include <deque> #include <stack> #include <bitset> #include <algorithm> #include <functional> #include <numeric> #include <utility> #include <sstream> #include <iostream> #include <iomanip> #include <cstdio> #include <cmath> #include <cstdlib> #include <ctime> #include <string> #include <cstring> using namespace std; vector<vector<int>> ans; vector<int> ans_item; void dfs(int lastF, int remain) { // lastF 上一阶段枚举的因子， remain = num/factor1/factor2/.../factorN //factor1 < factor2 <... < factorN < remain if (!ans_item.empty()) { ans_item.push_back(remain); ans.push_back(ans_item); ans_item.pop_back(); } for (int i = lastF; i < remain; i++) { if (remain / i < i) break; if (remain % i == 0) { //i是remain的因子 ans_item.push_back(i); dfs(i, remain / i); ans_item.pop_back(); } } } vector<vector<int>> getFactors(int n) { dfs(2, n); //n的因子从2开始 return ans; } int main() { getFactors(12); for (auto a : ans) { for (auto c : a) { cout << c<<" "; } cout << endl; } return 0; }
参考链接：http://zxi.mytechroad.com/blog/searching/leetcode-282-expression-add-operators/
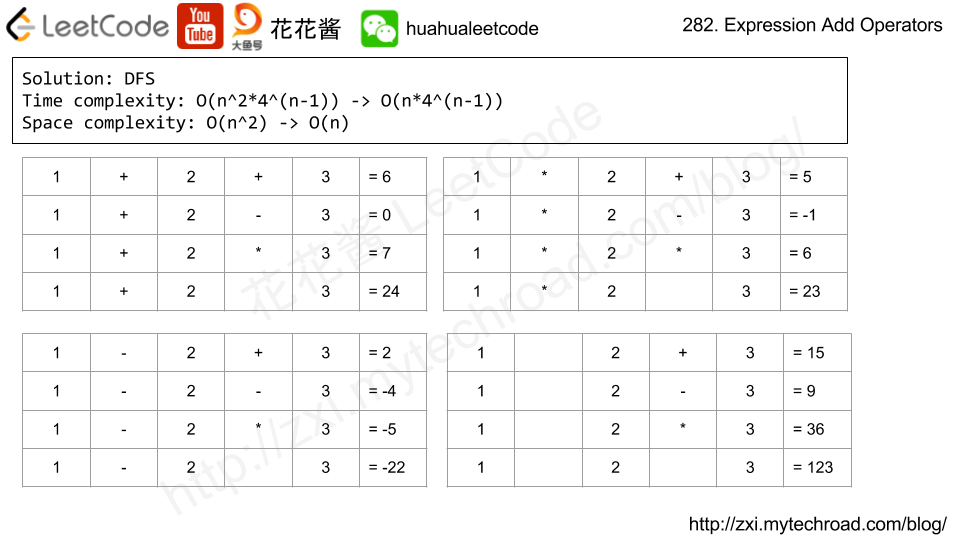
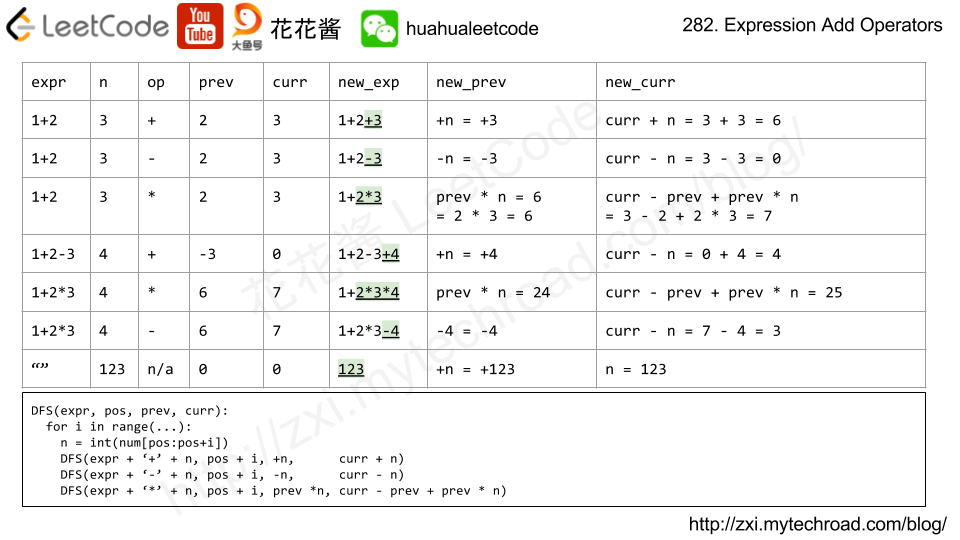
if * : curr = curr - prev + prev * n
特殊判断情况：
1) 第一个数字前不能有符号；
2）数字不能有前导0。
class Solution { public: vector<string> ans; vector<string> addOperators(string num, int target) { //DFS dfs(num, target, 0, "", 0, 0); return ans; } void dfs(string& num, int target, int pos, const string& exp, long prev, long curr){ if(pos == num.size()){ //终止条件：字符全处理完了 if(curr == target) ans.push_back(exp); return; } for(int l=1; l<=num.size()-pos; ++l){ //l枚举为第一个字符串的长度 string t = num.substr(pos, l); //从num中取出这个数 if(t[0]=='0' && t.size()>1) break; //0XXX... 前导0的情况 long n = stol(t); //string to long if(n > INT_MAX) break; //默认num不超过整型范围 if(pos == 0){ //第一个数字，特殊处理，没有operation操作 dfs(num, target, l, t, n, n); continue; } //第二个及以后的数字，需要考虑operation dfs(num, target, pos+l, exp+'+'+t, n, curr+n); dfs(num, target, pos+l, exp+'-'+t, -n, curr-n); dfs(num, target, pos+l, exp+'*'+t, prev*n, curr-prev+prev*n); } } };
// 优化时间复杂度：因为字符串的拼接操作，如：exp+'+'+t ； exp+'-'+t ； exp+'*'+t 是一个很大的开销。