一、拓扑排序的定义
1.AOV网:在一个表示工程的有向图中,用顶点表示活动,用弧表示活动之间的优先关系,这样的有向图为顶点表示活动的网,称为AOV网(Activity On Vertex Network)。
2.拓扑序列:设G={V,E}是一个具有n个顶点的有向图,V中的顶点序列v1,v2,...,vn,满足若从顶点vi到vj有一条路径,则在顶点序列中顶点vi必在vj之前,这样的顶点序列为一个拓扑序列。
3.拓扑排序:拓扑排序是对一个有向图构造拓扑序列的过程。构造时会有两个结果,如果此网的全部顶点都被输出,则说明它是不存在环(回路)的AOV网;如果输出的顶点少了,说明这个网存在环(回路),不是AOV网。
例如,
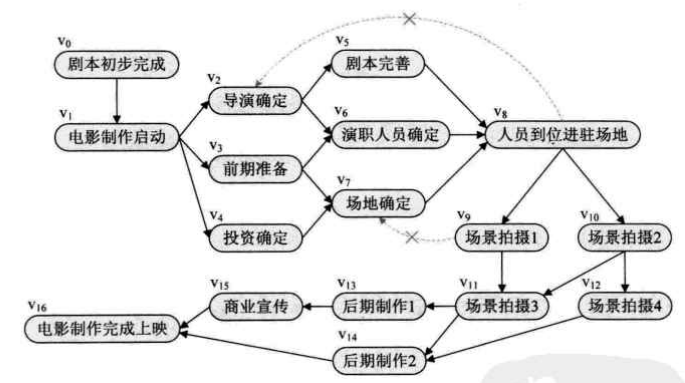
这样的AOV拓扑序列不止一条。序列v0v1v2v3v4v5v6v7v8v9v10v11v12v13v14v15v16是一个拓扑序列,序列v0v1v4v3v2v7v6v5v8v10v9v12v11v14v13v15v16。
二、拓扑排序算法
1.拓扑排序算法的基本思路:
从AOV网中选择一个入度为0的顶点输出,然后删去此顶点,并删除以此顶点为尾的弧,继续重复此步骤,直到输出全部顶点或者AOV网中不存在入度为0的顶点为止。
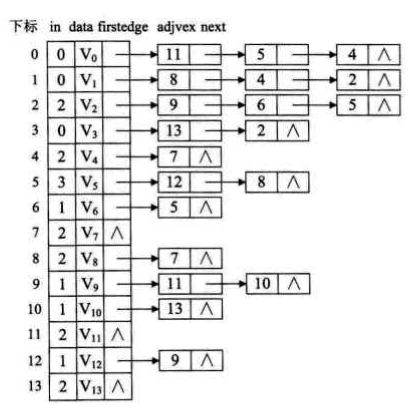
2.由于拓扑排序的过程中,需要删除顶点,显然用邻接表更加方便,因此需要创建一个邻接表。同时算法过程中始终要查找入度为0的顶点,因此在原来的顶点表结构中,增加一个入度域in,得到的顶点结点结构和边结点结构就是下面这样。
- 顶点表结点结构
package bigjun.iplab.topologicalSort; /** * 图的邻接表存储结构中的顶点结点类 */ public class VertexNode { public int in; // 顶点的入度 public Object data; // 顶点的符号信息 public EdgeNode firstEdge; // 指向第一条依附于该顶点的弧 public VertexNode(int in, Object data) { this(in, data, null); } public VertexNode(int in, Object data, EdgeNode firstEdge) { this.in = in; this.data = data; this.firstEdge = firstEdge; } }
- 边表结点结构
package bigjun.iplab.topologicalSort; /** * 用于拓扑排序算法中的邻接表存储结构中的边(或弧)结点类 */ public class EdgeNode { public int adjVex; // 该弧所指向的顶点在顶点数组中的下标 public EdgeNode nextEdge; // 指向下一条表示边或弧的结点类 public EdgeNode(int adjVex) { this(adjVex, null); } public EdgeNode(int adjVex, EdgeNode nextEdge) { this.adjVex = adjVex; this.nextEdge = nextEdge; } }
3.拓扑排序算法的C语言实现

#include "stdio.h" #include "stdlib.h" #include "io.h" #include "math.h" #include "time.h" #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 #define MAXEDGE 20 #define MAXVEX 14 #define INFINITY 65535 typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ /* 邻接矩阵结构 */ typedef struct { int vexs[MAXVEX]; int arc[MAXVEX][MAXVEX]; int numVertexes, numEdges; }MGraph; /* 邻接表结构****************** */ typedef struct EdgeNode /* 边表结点 */ { int adjvex; /* 邻接点域,存储该顶点对应的下标 */ int weight; /* 用于存储权值,对于非网图可以不需要 */ struct EdgeNode *next; /* 链域,指向下一个邻接点 */ }EdgeNode; typedef struct VertexNode /* 顶点表结点 */ { int in; /* 顶点入度 */ int data; /* 顶点域,存储顶点信息 */ EdgeNode *firstedge;/* 边表头指针 */ }VertexNode, AdjList[MAXVEX]; typedef struct { AdjList adjList; int numVertexes,numEdges; /* 图中当前顶点数和边数 */ }graphAdjList,*GraphAdjList; /* **************************** */ void CreateMGraph(MGraph *G)/* 构件图 */ { int i, j; /* printf("请输入边数和顶点数:"); */ G->numEdges=MAXEDGE; G->numVertexes=MAXVEX; for (i = 0; i < G->numVertexes; i++)/* 初始化图 */ { G->vexs[i]=i; } for (i = 0; i < G->numVertexes; i++)/* 初始化图 */ { for ( j = 0; j < G->numVertexes; j++) { G->arc[i][j]=0; } } G->arc[0][4]=1; G->arc[0][5]=1; G->arc[0][11]=1; G->arc[1][2]=1; G->arc[1][4]=1; G->arc[1][8]=1; G->arc[2][5]=1; G->arc[2][6]=1; G->arc[2][9]=1; G->arc[3][2]=1; G->arc[3][13]=1; G->arc[4][7]=1; G->arc[5][8]=1; G->arc[5][12]=1; G->arc[6][5]=1; G->arc[8][7]=1; G->arc[9][10]=1; G->arc[9][11]=1; G->arc[10][13]=1; G->arc[12][9]=1; } /* 利用邻接矩阵构建邻接表 */ void CreateALGraph(MGraph G,GraphAdjList *GL) { int i,j; EdgeNode *e; *GL = (GraphAdjList)malloc(sizeof(graphAdjList)); (*GL)->numVertexes=G.numVertexes; (*GL)->numEdges=G.numEdges; for(i= 0;i <G.numVertexes;i++) /* 读入顶点信息,建立顶点表 */ { (*GL)->adjList[i].in=0; (*GL)->adjList[i].data=G.vexs[i]; (*GL)->adjList[i].firstedge=NULL; /* 将边表置为空表 */ } for(i=0;i<G.numVertexes;i++) /* 建立边表 */ { for(j=0;j<G.numVertexes;j++) { if (G.arc[i][j]==1) { e=(EdgeNode *)malloc(sizeof(EdgeNode)); e->adjvex=j; /* 邻接序号为j */ e->next=(*GL)->adjList[i].firstedge; /* 将当前顶点上的指向的结点指针赋值给e */ (*GL)->adjList[i].firstedge=e; /* 将当前顶点的指针指向e */ (*GL)->adjList[j].in++; } } } } /* 拓扑排序,若GL无回路,则输出拓扑排序序列并返回1,若有回路返回0。 */ Status TopologicalSort(GraphAdjList GL) { EdgeNode *e; int i,k,gettop; int top=0; /* 用于栈指针下标 */ int count=0;/* 用于统计输出顶点的个数 */ int *stack; /* 建栈将入度为0的顶点入栈 */ stack=(int *)malloc(GL->numVertexes * sizeof(int) ); for(i = 0; i<GL->numVertexes; i++) if(0 == GL->adjList[i].in) /* 将入度为0的顶点入栈 */ stack[++top]=i; while(top!=0) { gettop=stack[top--]; printf("%d -> ",GL->adjList[gettop].data); count++; /* 输出i号顶点,并计数 */ for(e = GL->adjList[gettop].firstedge; e; e = e->next) { k=e->adjvex; if( !(--GL->adjList[k].in) ) /* 将i号顶点的邻接点的入度减1,如果减1后为0,则入栈 */ stack[++top]=k; } } printf(" "); if(count < GL->numVertexes) return ERROR; else return OK; } int main(void) { MGraph G; GraphAdjList GL; int result; CreateMGraph(&G); CreateALGraph(G,&GL); result=TopologicalSort(GL); printf("result:%d",result); return 0; }
4.拓扑排序算法的Java语言实现
实现类:
package bigjun.iplab.topologicalSort; import bigjun.iplab.linkStack.LinkStack; public class TopologicalSort { public static void TopoSort(DirectedNetwork G) throws Exception { int count = 0; // 统计输出顶点的个数 LinkStack S = new LinkStack(); for (int i = 0; i < G.getVexNum(); i++) {// 将入度为0的顶点入栈 if (G.getVexs()[i].in == 0) { S.stackPush(i); } } System.out.println("对AOV网进行拓扑排序得到打印结果为: "); while (!S.isStackEmpty()) { int i = (int) S.stackPop(); System.out.print(G.getVex(i) + "->"); count++; // 遍历顶点Vi的边链表,将每一个弧头对应的顶点的入度减1,也就是把Vi和连接自己的弧断开 for (EdgeNode edge = G.getVexs()[i].firstEdge; edge != null; edge = edge.nextEdge) { int k = edge.adjVex; if (--G.vexs[k].in == 0) { S.stackPush(k); } } if (count > G.getVexNum()) throw new Exception("这是一个有回环的图!"); } System.out.println("Over!"); } }
测试代码(以下图的AOV网为例):
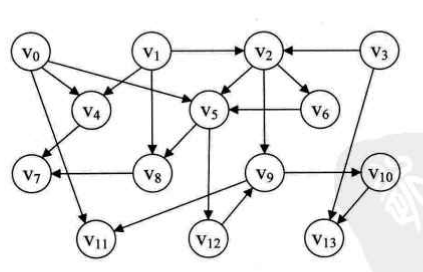
public static DirectedNetwork createDN_ForTopologicalSort() { EdgeNode e_0_4 = new EdgeNode(4); EdgeNode e_0_5 = new EdgeNode(5, e_0_4); EdgeNode e_0_11 = new EdgeNode(11, e_0_5); VertexNode v0 = new VertexNode(0, "V0", e_0_11); EdgeNode e_1_2 = new EdgeNode(2); EdgeNode e_1_4 = new EdgeNode(4, e_1_2); EdgeNode e_1_8 = new EdgeNode(8, e_1_4); VertexNode v1 = new VertexNode(0, "V1", e_1_8); EdgeNode e_2_5 = new EdgeNode(5); EdgeNode e_2_6 = new EdgeNode(6, e_2_5); EdgeNode e_2_9 = new EdgeNode(9, e_2_6); VertexNode v2 = new VertexNode(2, "V2", e_2_9); EdgeNode e_3_2 = new EdgeNode(2); EdgeNode e_3_13 = new EdgeNode(13, e_3_2); VertexNode v3 = new VertexNode(0, "V3", e_3_13); EdgeNode e_4_7 = new EdgeNode(7); VertexNode v4 = new VertexNode(2, "V4", e_4_7); EdgeNode e_5_12 = new EdgeNode(12); EdgeNode e_5_8 = new EdgeNode(8, e_5_12); VertexNode v5 = new VertexNode(3, "V5", e_5_8); EdgeNode e_6_5 = new EdgeNode(5); VertexNode v6 = new VertexNode(1, "V6", e_6_5); VertexNode v7 = new VertexNode(2, "V7"); EdgeNode e_8_7 = new EdgeNode(7); VertexNode v8 = new VertexNode(2, "V8", e_8_7); EdgeNode e_9_11 = new EdgeNode(11); EdgeNode e_9_10 = new EdgeNode(10, e_9_11); VertexNode v9 = new VertexNode(1, "V9", e_9_10); EdgeNode e_10_13 = new EdgeNode(13); VertexNode v10 = new VertexNode(1, "V10", e_10_13); VertexNode v11 = new VertexNode(2, "V11"); EdgeNode e_12_9 = new EdgeNode(12); VertexNode v12 = new VertexNode(1, "V12", e_12_9); VertexNode v13 = new VertexNode(2, "V13"); VertexNode[] vexs = {v0,v1,v2,v3,v4,v5,v6,v7,v8,v9,v10,v11,v12,v13}; int vertexNum = vexs.length; int edgeNum = 20; return new DirectedNetwork(vertexNum, edgeNum, vexs); } public static void main(String[] args) throws Exception { DirectedNetwork DN_ForTopoSort = createDN_ForTopologicalSort(); TopologicalSort.TopoSort(DN_ForTopoSort); }
输出:
对AOV网进行拓扑排序得到打印结果为:
V3->V1->V2->V6->V9->V10->V13->V0->V4->V5->V12->V8->V7->V11->Over!
结合例子分析代码执行过程:


初始化,count=0,遍历所有的顶点结点,将入度为0的结点的数组下标入栈,即S:0,1,3 然后进入while循环, -栈不为空,3出栈i等于3,打印V3,count=1,进入for循环,遍历v3的弧链表,k=13,将顶点v13的入度减1变为1,k=2,将顶点v2的入度减1变为1,将顶点v3上的弧删除
-栈不为空,1出栈i等于1,打印V1,count=2,进入for循环,遍历v1的弧链表,k=8,v8入度为1,k=4,v4入度为1,k=2,v2入度为0,将v2入栈,即S:2,0。将顶点v1上的弧删除
-其余同理
总结来说,为了保证弧尾的顶点在弧头之前被访问,拓扑排序算法的过程就是,先找入度为0的顶点(即最开始的弧尾),首先访问,访问完之后,将对应弧另一端的顶点的入度减1,并将这个弧删除,并继续找入度为0的点。
