1 前言
机器学习中,我们不能将全部数据用于模型训练,否则将没有数据集对模型进行验证,从而无法评估模型的预测效果。模型的评估方法主要是针对有监督学习的。
2 数据集划分方法
我们在拿到数据的时候,数据的表现形式会呈现多种多样性,我们首先需要做的是把数据格式化,把数据处理成计算机可以认识的结构。处理数据的过程叫做特征工程,特征工程是一个在机器学习的过程中,非常重要的一个过程,特征工程做的好坏,会直接影响到最后的模型准确度的一个上限。特征工程我后面会详细介绍,今天介绍的是在特征工程处理完后的,数据集的划分和性能的度量方式。
2.1 留出法Hold-out检验
整个数据集分成两部分:一部分用于训练,一部分用于验证,即训练集(training set)和测试集(test set)。
留出法直接将数据集D划分为两个互斥的部分,其中一部分作为训练集S,另一部分用作测试集 T。
通常训练集和测试集的比例为70%:30%。
同时,训练集、测试集的划分有两个注意事项:
1. 保证训练集和测试集的数据分布要相同。避免因数据划分过程引入的额外偏差而对最终结果产生影响。在分类任务中,保留类别比例的采样方法称为“分层采样”。
2. 采用若干次随机划分避免单次使用留出法的不稳定性。
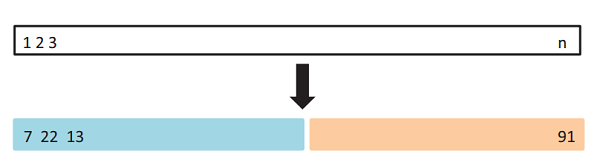
如上图所示,将左侧数据作为训练集(包含7、22、13等数据),将右侧数据作为测试集(包含91等),通过在训练集上训练模型,在测试集上观察不同模型不同参数对应的MSE的大小,就可以合适选择模型和参数了。
不过,这个简单的方法存在两个弊端:
1.最终模型与参数的选取将极大程度依赖于你对训练集和测试集的划分方法。
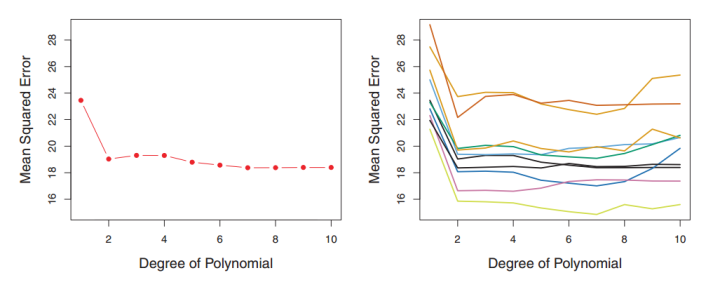
在不同的划分方法下,测试集中MSE的变动很大,对应的最优Degree也不一样。如果训练集和测试集的划分方法不够好,可能无法选择最好的模型与参数。
2.该方法只用了部分数据进行模型的训练。
当模型训练的数据量越大时,训练出来的模型通常效果会越好。训练集和测试集的划分意味着无法充分利用已有的数据,得到的模型效果也会受到一定的影响。
举例:
在分类任务中,万一将数据集中负类都划分到验证集中,模型的泛化能力就太弱了,在验证集上的划分就非常不准。
2.2 交叉验证(cross validation)
不是某一个方法名称,而是一类方法的统称。主要形式是把训练集分成两部分,一部分用来训练模型,另一部门用来验证模型,相当于一份数据集被分为训练集和验证集,主要是因为数据集中可能会有一些样本不平衡导致模型过拟合,增加验证集来验证模型,通过这种方法来了解模型的泛化能力。
交叉验证法先将数据集D划分为 $k$ 个大小相似的互斥子集,每次采用 $k−1$ 个子集的并集作为训练集,剩下的那个子集作为测试集。进行 $k$ 次训练和测试,最终返回 $k$ 个测试结果的均值。又称为“k折交叉验证”(k-fold cross validation)。
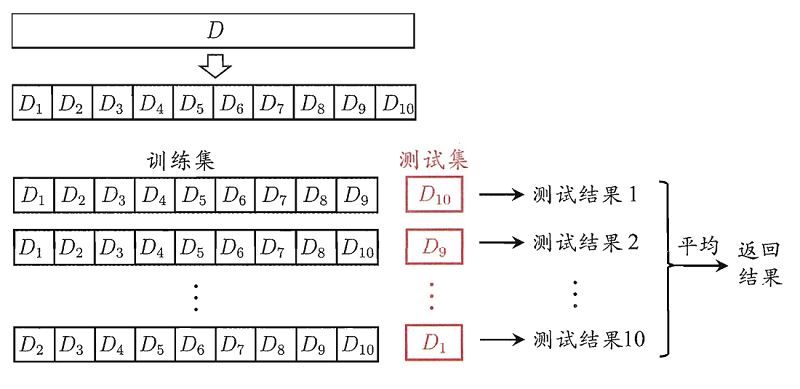
交叉验证方法:
1:留一法
2:k折交叉验证
2.2.1 留一法(leave-one-out,LOO)
留一法:也数据集分为训练集和测试集这一步骤。不同的是,我们现在只用一个数据作为测试集唯一元素,其他的数据都作为训练集,并将此步骤重复N次(N为数据集的数据数量)。
留一法是k折交叉验证 k=n( n为样本数)时候的特殊情况。即每次只用一个样本作测试集。该方法计算开销较大。
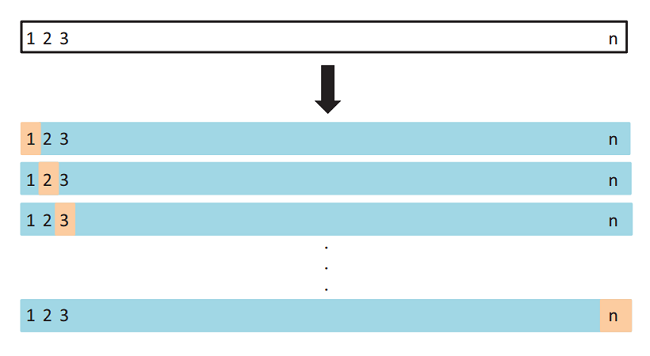
如上图所示,假设现有 n 个数据组成的数据集,那么 LOOCV 的方法就是每次取出一个数据作为测试集,其他 n-1 个数据都作为训练集用于训练模型和调参。结果就是我们最终训练了n个模型,每次都能得到一个MSE。计算最终测试集 MSE 则就是将这 n 个MSE取平均。
$CV_{(n)}=sum_{i=1}^{n}MSE_{i}$
2.2.2 K折交叉验证(K-fold Cross Validation)
和LOOCV的不同在于每次的测试集将不再只包含一个数据,而是多个,具体数目将根据K的选取决定。比如,如果K=5,那么我们利用五折交叉验证的步骤就是:
1.将所有数据集分成5份。
2.不重复地每次取其中一份做测试集,用其他四份做训练集训练模型,之后计算该模型在测试集上 MSEi 。
3.将5次的 MSEi 取平均得到最后的 MSE。
$CV_{(k)}=sum_{i=1}^{k}MSE_{i}$
举例:
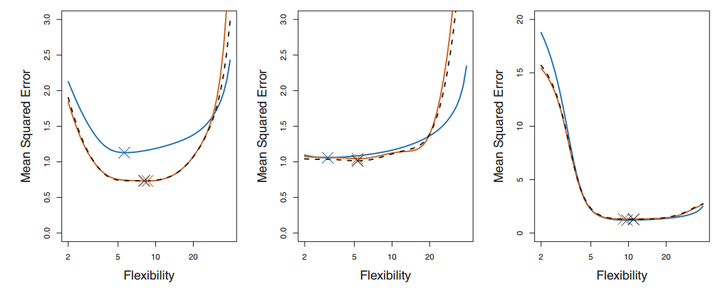
每一幅图种蓝色表示的真实的test MSE,而黑色虚线和橙线则分贝表示的是LOOCV方法和10-fold CV方法得到的test MSE。我们可以看到事实上LOOCV和10-fold CV对test MSE的估计是很相似的,但是相比LOOCV,10-fold CV的计算成本却小了很多,耗时更少。
我们要说说K的选取:一般来说,根据经验我们一般选择k=5或10。
3 自助法(bootstrapping)
自助法以自助采样为基础(有放回采样)。每次随机从 D 中挑选一个样本,放入 D ′ 中,然后将样本放回 D中,重复 m 次之后,得到了包含 m 个样本的数据集。
样本在m次采样中始终不被采到的概率是:
(1-frac{1}{m})^{m}
取极限得:
$lim_{m->infty}(1-frac{1}{m})^{m}=frac{1}{e}=0.368$
即 D 中约有36.8%的样本未出现在D ′ 中。于是将 D ′ 用作训练集, D D ′ 用作测试集。这样,仍然使用 m 个训练样本,但约有1/3未出现在训练集中的样本被用作测试集。
优点:自助法在数据集较小、难以有效划分训练/测试集时很有用。
缺点:然而自助法改变了初始数据集的分布,这回引入估计偏差。
4 性能度量
二分类问题常用的评价指标时查准率和查全率。
根据预测正确与否,将样例分为以下四种:
TP(True positive,真正例)——将正类预测为正类数。
FP(False postive,假正例)——将反类预测为正类数。
TN(True negative,真反例)——将反类预测为反类数。
FN(False negative,假反例)——将正类预测为反类数。
(1)精确率(precision):
$P=frac{TP}{TP+FP}$
即将正类预测为正类数与预测为正类的总数的比值。
(2)召回率(recall)
$P=frac{TP}{TP+FN}$
即将正类预测为正类数与正类总数的比值。
精确率和召回率是一对矛盾的度量。F1 是查准率和查全率的调和平均:
$frac{1}{F_{1}}=frac{1}{2}(frac{1}{P}+frac{1}{R})$
$F_{1}=frac{2PR}{P+R}$
当精确率和召回率都高时, F1也会高。
参考文献: