线性回归的从零开始实现

1 导入实验所需要的包

import torch
import numpy as np
import matplotlib.pyplot as plt
from torch import nn
from IPython import display
#解决内核挂掉
import os
os.environ["KMP_DUPLICATE_LIB_OK"]  =  "TRUE"

2 生成数据集

　　将根据带有噪声的线性模型构造一个人造数据集。任务是使用这个有限样本的数据集来恢复这个模型的参数。这里使用低维数据，这样可以很容易地将其可视化。

　　在下面的代码中, 将生成一个包含 1000 个样本的数据集，每个样本包含从标准正态分布中采样的 2 个特征。合成数据集是一个矩阵 $mathbf{X} in mathbb{R}^{1000 imes 2} $ 。
　　使用线性模型参数 $ mathbf{w}=[2,-3.4]^{ op}$ 、 $b=4.2$ 和噪声项 $epsilon$  生成数据集及其标签:

　　　　$mathbf{y}=mathbf{X} mathbf{w}+b+epsilon$

　　可以将 $epsilon$ 视为捕获特征和标签时的潜在观测误差。在这里认为标准假设成立，即 $epsilon $ 服从均值为 $0$ 的正态分布。为了简化问题, 我们将标准差设 为 $0.01 $ 。下面的代码生成合成数据集。

def get_random_data(w,b,num_example):
    X = torch.normal(0,1,(num_example,len(w)))
    #X = torch.normal(0,1,(num_example,2))
    Y = torch.matmul(X,w)+b      #矩阵乘法，要求稍微低一点   
    Y += torch.normal(0,0.01,Y.shape)
    return X,Y.reshape(-1,1)

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = get_random_data(true_w, true_b, 1000)

torch.mm(mat1, mat2, out=None) → Tensor

torch.matmul(mat1, mat2, out=None) → Tensor

对矩阵mat1和mat2进行相乘。 如果mat1 是一个n×m张量，mat2 是一个 m×p 张量，将会输出一个 n×p 张量out。

参数 ：

mat1 (Tensor) – 第一个相乘矩阵

mat2 (Tensor) – 第二个相乘矩阵

features.shape, labels.shape

(torch.Size([1000, 2]), torch.Size([1000, 1]))

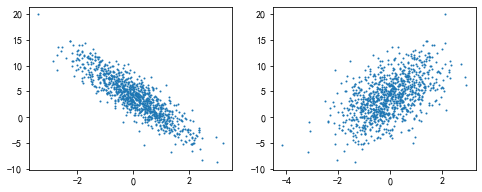
3 可视化初始数据

# 设置图的尺寸
plt.rcParams['figure.figsize'] = (8,3)
plt.subplot(1,2,1) #要生成两行两列，这是第一个图plt.subplot('行','列','编号')
plt.scatter(features[:,1].detach().numpy(), labels.detach().numpy(),s=1);
plt.subplot(1,2,2) 
plt.scatter(features[:,0].detach().numpy(), labels.detach().numpy(),s=1);

　　　　　　

labels.detach().numpy().shape
(1000, 1)

features[:,1].detach().numpy().shape
(1000,)

4 读取数据集

　　在下面的代码中，我们定义一个 data_iter 函数， 该函数接收批量大小、特征矩阵和标签向量作为输入，生成大小为 batch_size 的小批量。每个小批量包含一组特征和标签。

def data_iter(batch_size,features,labels):
    num_example = len(features)
    indices = list(range(num_example))
    np.random.shuffle(indices)
    for i in range(0, num_example, batch_size):
        batch_indices = torch.tensor(indices[i: min(i + batch_size, num_example)])
#         print("batch_indices=",batch_indices)
        yield features[batch_indices], labels[batch_indices]
        #采用yield 循环并没有结束，而是暂时”停止“，返回的是一个迭代器

# next(data_iter(50,features,labels))
# next(data_iter(50,features,labels))

　　测试一下：读取第一个小批量数据样本并打印。每个批量的特征维度说明了批量大小和输入特征数。 同样的，批量的标签形状与batch_size相等。

batch_size = 10

for X, y in data_iter(batch_size, features, labels):
    print("features=",X, '
labels=', y)
    break

features= tensor([[-1.3117,  0.0544],
        [-2.1899, -0.9396],
        [ 0.2574,  0.5958],
        [-0.1184,  0.9712],
        [ 1.2400,  0.7710],
        [ 1.2233,  0.3990],
        [-1.3850, -0.8254],
        [-3.0746,  0.2081],
        [ 0.3196, -0.3576],
        [-1.8893, -0.6696]]) 
labels= tensor([[ 1.3906],
        [ 3.0155],
        [ 2.6977],
        [ 0.6439],
        [ 4.0464],
        [ 5.2818],
        [ 4.2274],
        [-2.6520],
        [ 6.0649],
        [ 2.6800]])

5 初始化模型参数

w = torch.normal(0,0.01,size=(2,1),requires_grad=True)
b = torch.zeros(1,requires_grad=True)

6 定义模型

　　需计算输入特征 $X$ 和模型权重 $w$ 的矩阵向量乘法后加上偏置 $b $。需要注意的是当我们用一个向量加一个标量时，标量会被加到向量的每个分量上。

def linear(X,w,b):
    return (torch.matmul(X,w)+b).reshape(-1,1)

7 定义损失函数

def MSE_loss(y_hat,y):
    return ((y_hat- y )**2)/2

8 定义优化算法

def mini_batch_sgd(params,lr,batch_size):
    """小批量随机梯度下降。"""
    #torch.no_grad() 是一个上下文管理器，被该语句 wrap 起来的部分将不会track 梯度。
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()   #梯度清零

9 训练

lr = 0.003
num_epoch = 20
net = linear
loss = MSE_loss

for epoch in range(num_epoch):
    for X , y in data_iter(batch_size, features, labels):
        y_hat = net(X,w,b)
        cur_loss = loss(y_hat,y)
#         print("cur_loss = ",cur_loss)
        cur_loss.sum().backward()
#         print("cur_loss.sum()=",cur_loss.sum())
#         print(w.grad)
#         print(torch.no_grad())
        mini_batch_sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

10 输出权重和偏置

w.detach().numpy()

array([[ 1.9997293],
       [-3.4006505]], dtype=float32)

b.detach().numpy()

array([4.1997237], dtype=float32)

看完点个关注呗！！_{（总结不易）}