BZOJ1774: [Usaco2009 Dec]Toll 过路费

n<=250个点m<=10000边无自环图，有点权边权，Q<=10000个询问i到j的最短路。这里的路径长度指路上边权和+路上点权最大值。

n这么小，询问这么多，那就跑跑floyd吧！f[i][j]记最短路，g[i][j]记最短路上最大点权，当f[i][j]+g[i][j]>f[i][k]+f[k][j]+max(g[i][k],g[k][j])时更新答案，注意不要用无效状态即可。

#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<iostream>
using namespace std;
 
int n,m,q;
#define maxn 261
int f[maxn][maxn],g[maxn][maxn];
int x,y,v;
const int inf=5e8;
int max(int a,int b) {return a>b?a:b;}
int min(int a,int b) {return a<b?a:b;}
int main()
{
    scanf("%d%d%d",&n,&m,&q);
//  for (int i=1;i<=n;i++)
//      for (int j=1;j<=n;j++)
//          g[i][j]=inf;
    memset(g,0,sizeof(g));
    for (int i=1;i<=n;i++) scanf("%d",&g[i][i]);
    for (int i=1;i<=n;i++)
    {
        for (int j=1;j<=n;j++)
            f[i][j]=inf;
        f[i][i]=0;
    }
    for (int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&x,&y,&v);
        g[x][y]=max(g[x][x],g[y][y]);
        g[y][x]=max(g[x][x],g[y][y]);
        f[x][y]=min(f[x][y],v);
        f[y][x]=min(f[y][x],v);
    }
//  for (int i=1;i<=n;i++){
//      for (int j=1;j<=n;j++)
//          cout<<f[i][j]<<' ';cout<<endl;}cout<<endl;
//  for (int i=1;i<=n;i++){
//      for (int j=1;j<=n;j++)
//          cout<<g[i][j]<<' ';cout<<endl;}cout<<endl;
    for (int k=1;k<=n;k++)
        for (int i=1;i<=n;i++)
            for (int j=1;j<=n;j++)
                if (!g[i][j] || (g[i][k] && g[k][j] && f[i][j]+g[i][j]>f[i][k]+f[k][j]+max(g[i][k],g[k][j])))
                {
                    f[i][j]=f[i][k]+f[k][j];
                    g[i][j]=max(g[i][k],g[k][j]);
                }
//  for (int i=1;i<=n;i++){
//      for (int j=1;j<=n;j++)
//          cout<<f[i][j]<<' ';cout<<endl;}cout<<endl;
//  for (int i=1;i<=n;i++){
//      for (int j=1;j<=n;j++)
//          cout<<g[i][j]<<' ';cout<<endl;}cout<<endl;
    for (int i=1;i<=q;i++)
    {
        scanf("%d%d",&x,&y);
        printf("%d
",f[x][y]+g[x][y]);
    }
    return 0;
}

错误！本题中的最短路，枚举中转点顺序的不同会产生不同的答案。观察下图，4-5的“最短路”是2+4+9+10=25，而这需要先用到路径1-3-5（以3为中转点），再以1为中转点更新答案。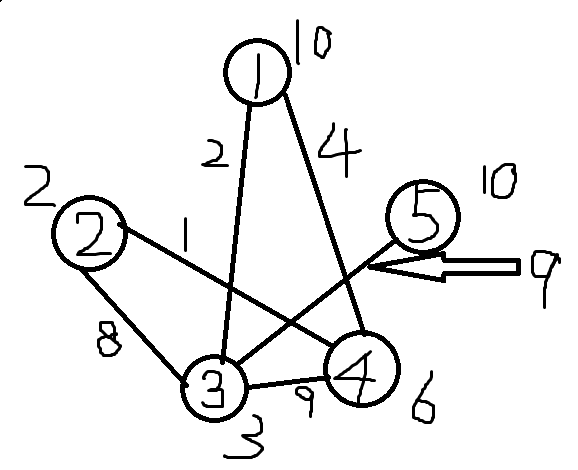

不过本题的“最短路”是有赖于图的最短路的，在最短路可以随便枚举中转点的前提下，优先考虑小权点会使最优答案被及时地更新。就是说，f[i][j]记最短路，g[i][j]记答案，从小权点到大权点枚举中转点，一边更新答案。

当然最后不要忘了有重边。。。。

#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<math.h>
//#include<iostream>
using namespace std;

int n,m,q;
#define maxn 261
int f[maxn][maxn],g[maxn][maxn];
int x,y,v;
const int inf=1e9;
int max(int a,int b) {return a>b?a:b;}
int min(int a,int b) {return a<b?a:b;}
int a[maxn];
struct Point{int id,v;bool operator < (const Point &b) const {return v<b.v;}}p[maxn];
int main()
{
    scanf("%d%d%d",&n,&m,&q);
    for (int i=1;i<=n;i++)
        for (int j=1;j<=n;j++)
            f[i][j]=g[i][j]=inf;
    for (int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        g[i][i]=p[p[i].id=i].v=a[i];
        f[i][i]=0;
    }
    sort(p+1,p+1+n);
    for (int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&x,&y,&v);
        if (v<f[x][y]) f[x][y]=f[y][x]=v;
    }
    for (int k=1;k<=n;k++)
        for (int i=1;i<=n;i++)
            for (int j=1;j<=n;j++)
            {
                int x=p[k].id;
                f[i][j]=min(f[i][j],f[i][x]+f[x][j]);
                g[i][j]=min(g[i][j],f[i][j]+max(p[k].v,max(a[i],a[j])));
            }
    for (int i=1;i<=q;i++)
    {
        scanf("%d%d",&x,&y);
        printf("%d
",g[x][y]);
    }
    return 0;
}