Codeforces713D. Animals and Puzzle

$n<=1000,m<=1000$，$n*m$的01矩阵，给$t<=1000000$个询问，每次问一个矩形中最大的1正方形的边长。

先想想不考虑“一个矩形中”的限制，那记$f(i,j)$--以$(i,j)$为右下角的最大的正方形，那

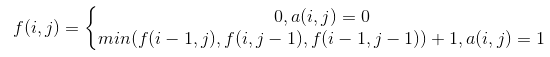
很好，那现在加入一个边界限制，由于边长r的正方形同时也是边长r-1，r-2……的，那来二分答案吧，现在对二分的答案$x$就检查一个区域里的$f$数组中最大的那一个是否大于等于$x$。查静态区间最大，用ST表啦！拓展到二维情况即可。

#include<string.h>
#include<stdlib.h>
#include<stdio.h>
//#include<math.h>
//#include<assert.h>
#include<algorithm>
//#include<iostream>
//#include<bitset>
using namespace std;

int n,m,t;
#define maxn 1011
int a[maxn][maxn],Log[maxn];short rmq[maxn][maxn][12][12];

int x1,x2,y1,y2;
int rmqquery(int x1,int y1,int x2,int y2)
{
    int p=Log[x2-x1+1],q=Log[y2-y1+1];
    return max(max(rmq[x1][y1][p][q],rmq[x2-(1<<p)+1][y1][p][q])
    ,max(rmq[x1][y2-(1<<q)+1][p][q],rmq[x2-(1<<p)+1][y2-(1<<q)+1][p][q]));
}
bool check(int len) {return rmqquery(x1+len-1,y1+len-1,x2,y2)>=len;}
int main()
{
    scanf("%d%d",&n,&m);
    for (int i=1;i<=n;i++)
        for (int j=1;j<=m;j++)
            scanf("%d",&a[i][j]);
    for (int i=1;i<=n;i++)
        for (int j=1;j<=m;j++)
            if (a[i][j]==0) rmq[i][j][0][0]=0;
            else rmq[i][j][0][0]=min(rmq[i][j-1][0][0],min(rmq[i-1][j][0][0],rmq[i-1][j-1][0][0]))+1;
    Log[0]=-1; for (int i=1,to=max(n,m);i<=to;i++) Log[i]=Log[i>>1]+1;
    for (int q=1;(1<<q)<=m;q++)
        for (int i=1;i<=n;i++)
            for (int j=1,to=m-(1<<q)+1;j<=to;j++)
                rmq[i][j][0][q]=max(rmq[i][j][0][q-1],rmq[i][j+(1<<(q-1))][0][q-1]);
    for (int p=1;(1<<p)<=n;p++)
    {
        for (int i=1,to=n-(1<<p)+1;i<=to;i++)
            for (int j=1;j<=m;j++)
                rmq[i][j][p][0]=max(rmq[i][j][p-1][0],rmq[i+(1<<(p-1))][j][p-1][0]);
        for (int q=1;(1<<q)<=m;q++)
            for (int i=1,to=n-(1<<p)+1;i<=to;i++)
                for (int j=1,to=m-(1<<q)+1;j<=to;j++)
                    rmq[i][j][p][q]=max(rmq[i][j][p][q-1],rmq[i][j+(1<<(q-1))][p][q-1]);
    }
    scanf("%d",&t);
    while (t--)
    {
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
        int L=0,R=min(x2-x1+1,y2-y1+1);
        while (L<R)
        {
            const int mid=(L+R+1)>>1;
            if (check(mid)) L=mid;
            else R=mid-1;
        }
        printf("%d
",L);
    }
    return 0;
}