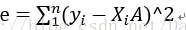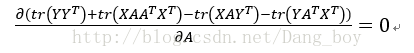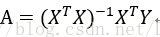岭回归&Lasso回归

转自:https://blog.csdn.net/dang_boy/article/details/78504258

https://www.cnblogs.com/Belter/p/8536939.html

https://www.cnblogs.com/Belter/p/8536939.html  （这个也写的很好，只不过还没看）

1.最小二乘法则

假设我们有n个样本数据，每个数据有p个特征值，然后p个特征值是线性关系。

即对应的线性模型

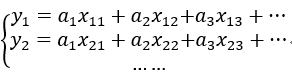
写成矩阵的形式即是Y=XA，误差B矩阵：即B=Y-XA。【Y和A是列向量，X是矩阵】

误差的平方的计算公式

Xi为行向量，A为列向量。

最小二乘法的目标就是取得最小的e对应的A，由于方差的计算是一个二次函数，即抛物线，对应存在一个最小值，即导数为0对应的A。所以对e求A的偏导数，再使其等于0，求解方程即可以获得A。

误差的平方e写成矩阵形式即为

对矩阵E取迹（迹就是矩阵对角线上所有元素的累加）且对迹求导后结果为一个矩阵。

即为 

展开为  

求导化简结果为

注：这个计算的过程是涉及到向量的求导运算，看了好长时间实在是看不懂。也不知道这个结果是怎么计算出来的，暂且记住吧。。

参考：https://blog.csdn.net/lipengcn/article/details/52815429

当A的维数比Y的维数多，即样本数量n少于特征值p的时候存在多个解，可能导致结果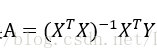很不稳定，所以要确保n>p。

X矩阵不存在广义逆（即奇异性）的情况：
1）X本身存在线性相关关系（即多重共线性），即非满秩矩阵。
当采样值误差造成本身线性相关的样本矩阵仍然可以求出逆阵时，此时的逆阵非常不稳定，所求的解也没有什么意义。
2）当变量比样本多，即p>n时.
这时，回归系数会变得很大，无法求解。在统计学上，可证明A的最小二乘解为无偏估计，即多次得到的采样值X而计算出来的多个系数估计值向量 的平均值将无限接近于真实值向量β。

2.岭回归

那么解决不存在矩阵广义逆：

在误差矩阵加上一个对A的L2范数控制系数矩阵，

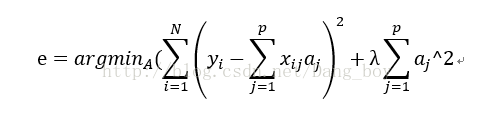
而LASSO回归是加上的L1范数作为正则项。

反映到矩阵上，就是在原先的A的最小二乘估计中加一个小扰动λI，

变为满秩矩阵，可以求稳定的逆。

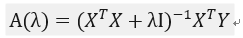
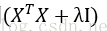
具体推导过程就不贴了，贴了也看不懂。 

3.LASSO回归

 

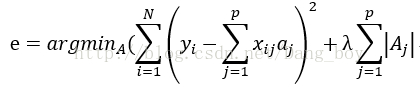
只是在于正则项的不同。

4.对于偏差与方差的理解

看到这个图觉得很不错：

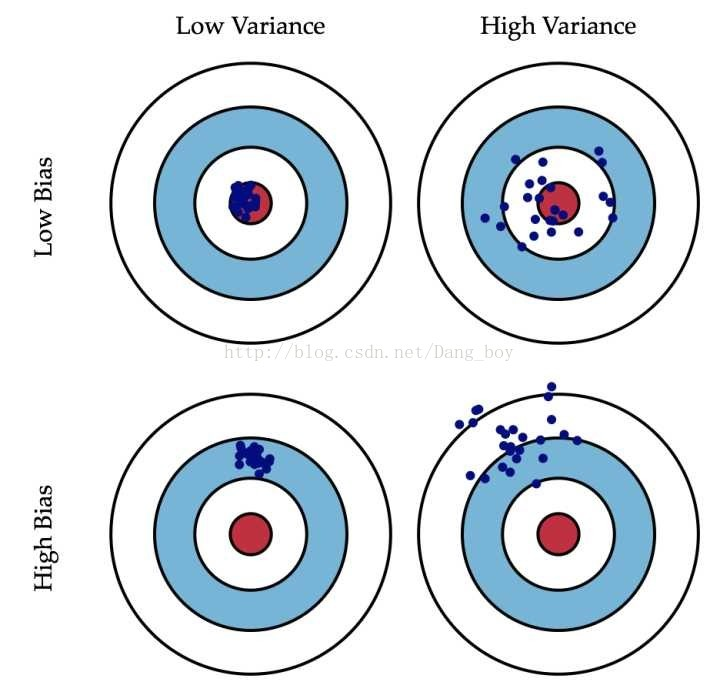
偏差：预测出来的数据与真实值的差距

方差：预测出来的数据的分散程度