1.神经网络模型1

图1
这是一个神经网络的模型,通常设置一个x0,作为偏执单元或者偏置(bias)神经元。
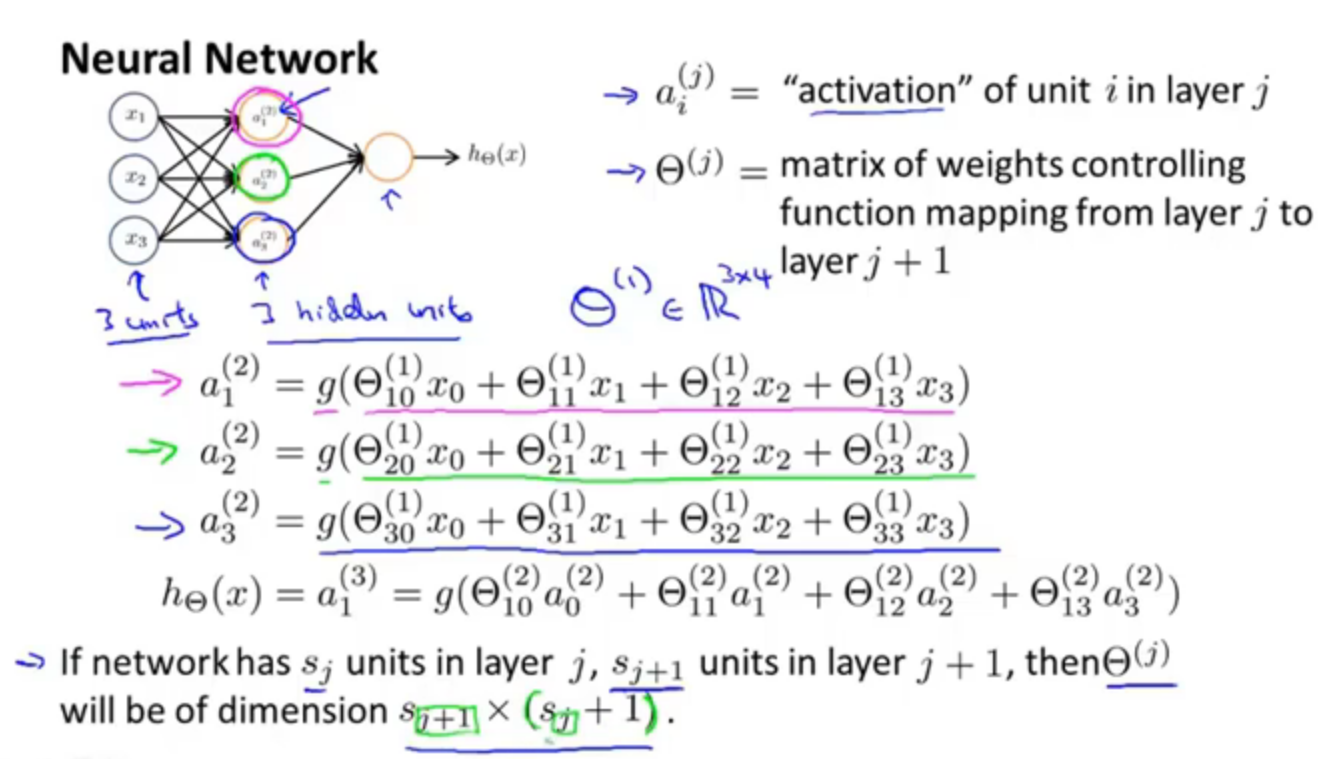
图2
这里最后一句话,说的是系数矩阵θ,神经网络模型中,如果当前在j层有s_j个单元,在j+1层有s_j+1个单元,那么第j层的系数矩阵theta_j,是s_j+1(s_j +1)维的。
//就像图中,三个公式,应该是每层其实都有一个偏置单元。s_j+1是因为输入层得到的结果要是隐含层的输入,隐含层有s_j+1个单元,(s_j +1)是+上本层的偏置单元。
2.神经网络中的分类问题
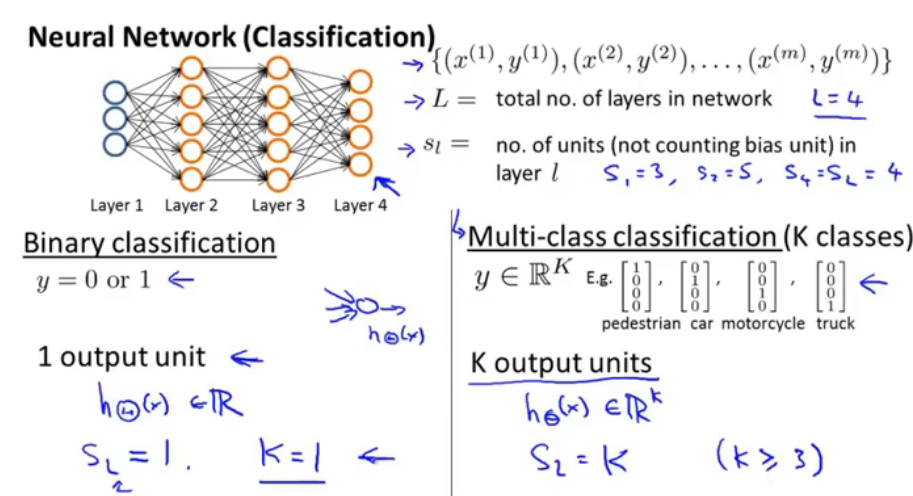
图3
对于二分类的问题,输出层只有一个输出单元,对于多分类问题(k≥3),那么输出层就有k个输出单元。
3.神经网络的代价函数

图4
首先第一项是对输出层的输出求和,每个都乘上yk;正则项,theta右上角的(l)表示的是层数,j表示的是第j行吧,也就是一共s_j+1行,i表示的是s_j列,那么一共是L-1层的相加。每一层都加上了一个偏置,但是在图中并没有画出。通常正则化项都不把偏置项加入到其中,但是加入了之后影响也不大。
4.反向传播算法
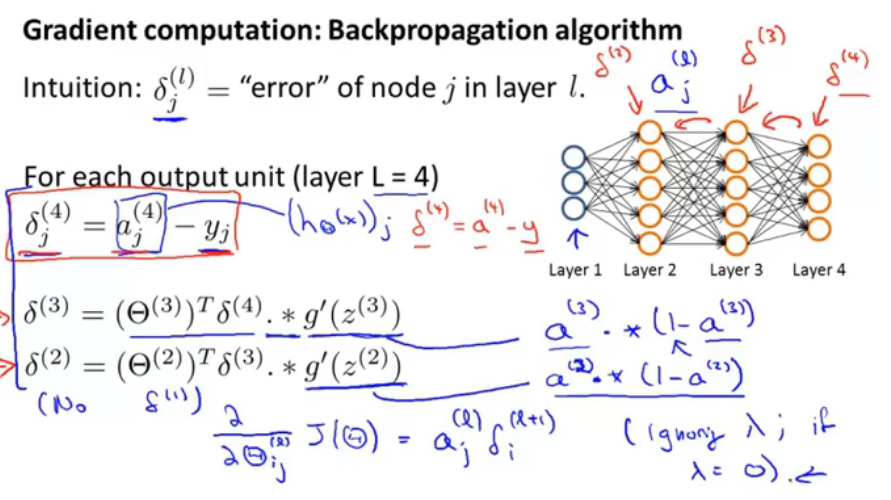
图5
首先就是需要计算每个单元的误差,怎么计算呢?如图,输出层也就是第4层,就等于当前的计算结果-实际结果;第三层的误差,第三层权重矩阵转置*第四层误差向量*激活函数的导数。
图中还给了一个公式就是——求偏导项的公式——代价函数的对每层权重矩阵单个,求导的公式=l层第j个节点的值*l+1层第i个节点的误差。 (证明过程十分复杂)
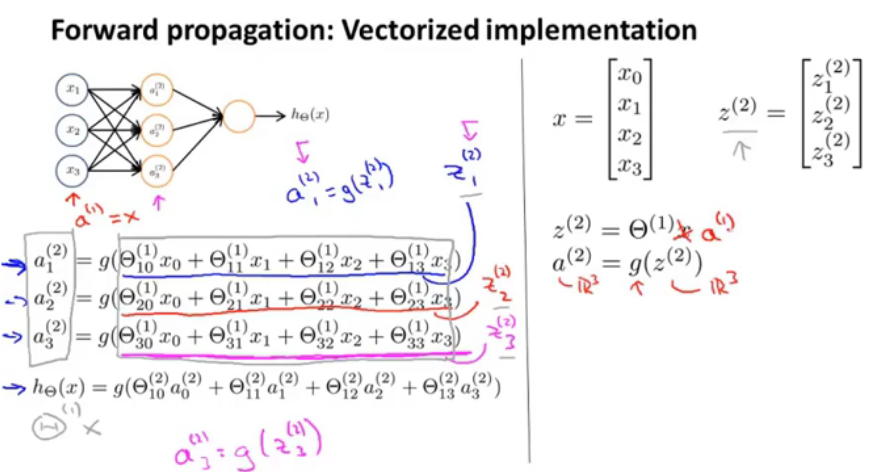
图7
z这里代表的是:每层的计算结果,代入激活函数之后就可以作为下一层神经元的输入。是三维的。
以下为伪代码:

图8
将所有误差(三角形的是希腊字符delta的大写形式)都初始化为0,循环m次,最终▲(l)_ij得到的是m个样本中a(l)j▲(l+1)i之和(也就是偏导数之和)。红笔圈画部分是将其转化成矩阵形式的运算,那这么说这个大三角形就应该是(l+1)*(l),因为它正是用来计算。得出代价函数的所有偏导数之后,就可以使用递归下降或者其他的方法来计算。

图9
1.误差=代价函数对中间项的偏导数,反向传播算法是反向计算每个点的误差。
2.如图中红框内的内容,反向传播时如何计算第二层第二个单元误差,那么就是根据反向来计算,绿色部分是计算第三层第二个单元的,也是权重和下一层的单元的误差求和。这是一个反向计算的过程。
5.梯度检测
为了确保使用BP算法得到的梯度矩阵是正确的,那么就使用手动计算的方法来通过计算导数来判断是否相等。
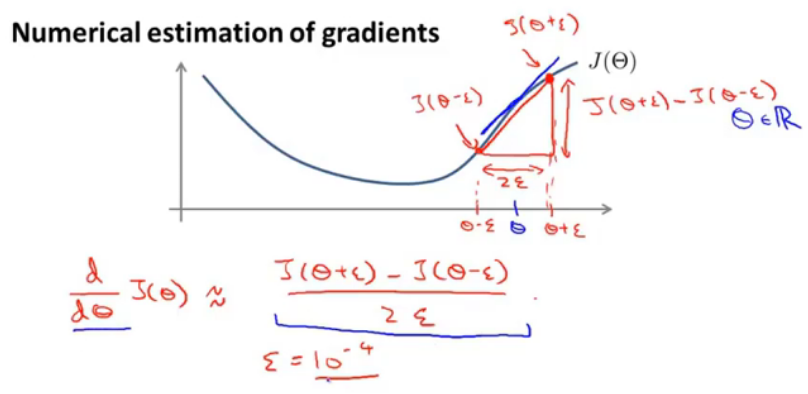
图10
使用数值方法来估计,在theta旁选一个很小的epsilon,那么下边的红色部分就是计算theta点的导数的公式。同样的道理对向量θ来说:

图11.计算导数
这些公式就是进行梯度检测,其中theta可能是神经网络中系数矩阵(权重矩阵)展开的结果,对theta中的每一个数(分量)求导。

图12.梯度检测算法
for循环,从1到n,前两句=计算theta_i+epsilon,后两句=theta_i-epsilon,再通过计算gradApprox,计算出大约梯度,再与DVec(BP算法中得到的)进行比较,如果大约相等的话, 就可以保证BP算法运行正确,但是在进行BP算法训练分类器之前就要确保此算法不再执行,因为它的执行速度非常慢。
6.随机初始化

图13.theta初始化为什么?
在计算时需要使用初始化的theta,并且根据这个去使用BP算法来进行更新,最终得到theta,那么初试的theta设置成什么呢?初始化为0?这在逻辑回归中是可以的,但是BP算法中却不可以。
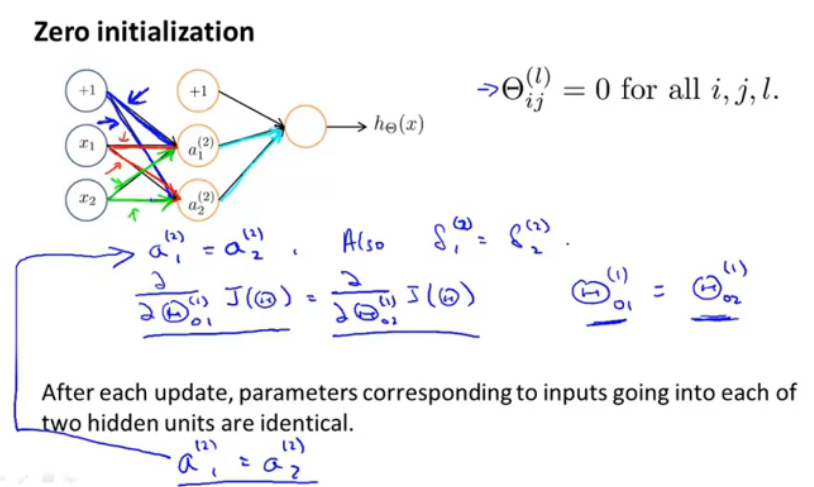
图14.初始化情况(相等)
如果将theta全部初始为0,那么图中蓝色线,绿色线,红色线,不论如何更新,各自都始终保持相等,对theta_01,theta_02偏导数相等,那么更新后的值也会保持相等,所以要使用随机初始化方法:

图15.随机初始化,打破对称
对每一个进行随机初始化到区间内,具体操作如15中下两式, 随机化创建一个10行11列的矩阵,值在[0,1],并且*2*epsilon-epsilon,那么最终值在[-ε,ε]之间。
7.总体回顾
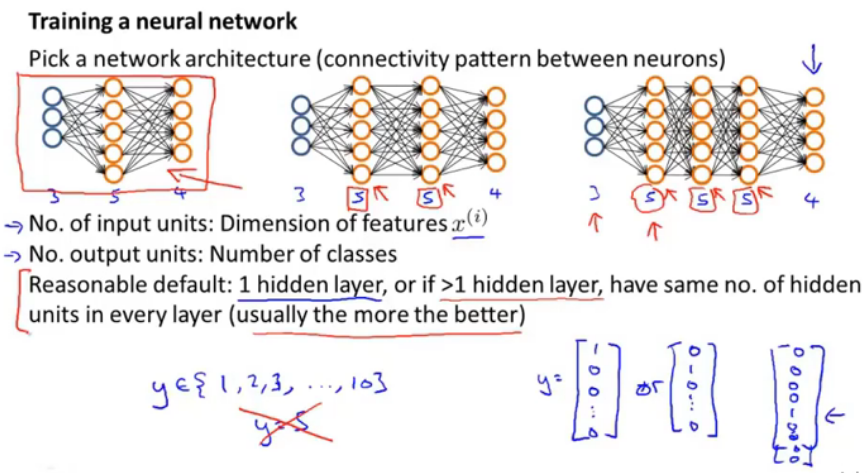
图16.选择一个神经网络模型
输入层中输入单元的个数就是特征的维数,输出层中输出单元的个数就是类别数;一些原则:最好隐含层只有一层,或者是多个隐含层并且每层的数目都相同,通常来说隐含层越多越好,但是计算量会变大;假如y有十个取值,那么输出层中输出单元个数就是10,并且若y=5,那么y=[0,0,0,0,1....]T,这样的取值。

图17.训练一个神经网络
初始化权重;使用前向算法获得对应输出结果;计算代价函数;使用后向算法来计算偏导数;实现时使用了for循环,对每一个样例来说都能进行上述的整个过程,整个过程重复了m次。

图18.训练一个神经网络
使用梯度下降检测BP中的梯度矩阵值,并且停止梯度检测算法;使用梯度下降或者其他最优化算法来使J(θ)变得最小。从下图中就可以看出:
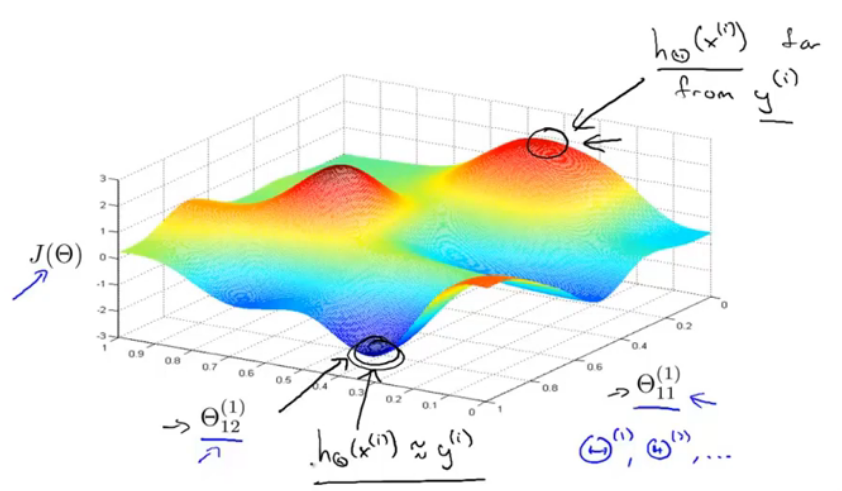
图19.梯度下降的直观表示
当取到最小值时,也就是代价函数最小,那么模型输出与期望输出之间差值是最小的;当J(θ)很大时,二者相差很大,所以使用梯度下降一般可以得到最小值(局部最小值)。