对正整数n,欧拉函数是小于或等于n的数中与n互质的数的数目。此函数以其首名研究者欧拉命名,它又称为Euler's totient function、φ函数、欧拉商数等。例如:φ(8) = 4(Phi(8) = 4),因为1,3,5,7均和8互质。
S(n) = Phi(1) + Phi(2) + ...... Phi(n),给出n,求S(n),例如:n = 5,S(n) = 1 + 1 + 2 + 2 + 4 = 10,定义Phi(1) = 1。由于结果很大,输出Mod 1000000007的结果。
Input
输入一个数N。(2 <= N <= 10^10)
Output
输出S(n) Mod 1000000007的结果。
Input示例
5
Output示例
10
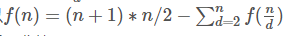
菜鸡只能背结论,证明去tls那里看啊
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N=5000005,MD=1e9+7,INV2=500000004; bool is_p[N]; int pri[N],phi[N]; int tot; unordered_map<ll,ll>M; void init() { tot=0,phi[0]=0,phi[1]=1; for(int i=2; i<N; i++) { if(!is_p[i])pri[tot++]=i,phi[i]=i-1; for(int j=0; j<tot&&pri[j]*i<N; j++) { is_p[pri[j]*i]=1; if(i%pri[j]==0) { phi[i*pri[j]]=phi[i]*pri[j]; break; } phi[i*pri[j]]=phi[i]*(pri[j]-1); } } for(int i=1; i<N; i++) phi[i]=(phi[i]+phi[i-1])%MD; } ll cal(ll a) { if(a<N)return phi[a]; if(M.count(a)) return M[a]; ll ans=a%MD*((a+1)%MD)%MD*INV2%MD; for(ll l=2,r; l<=a;l=r+1) { r=a/(a/l); ans=(ans-(r-l+1)%MD*cal(a/l)%MD)%MD; } M[a]=ans; return ans; } int main() { ll a; init(); cin>>a; cout<<(cal(a)+MD)%MD; return 0; }