归并排序
时间复杂度:O(log2n)
流程
1.分界点为中点:mid=(left + right)/2
2.分别递归排序两边
3.归并——合二为一 O(n)

这里我们就得到了两个排好序(从小到大),然后:
- 再开出一个数组res,用i,j两个指针分别指向第一个第二个的开头
- 比较i1与j1,不妨设i1小于j1,这时将i1放进res的第一个位置
- 将i指针右移一位,指向i2
- 比较i2与j1,不妨设j1小于i2,这时就将j1>放人res的第二位
- 如此类推…
- 如果当某一段的数放完了,另一段还有元素的话就直接把另一端的元素全部放进res的尾端
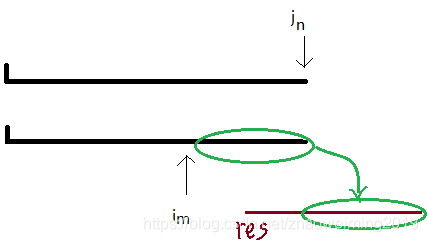
//归并部分
while(i<=mid && j<=r)
{
if(q[i]<=q[j])
{
res[k++]=q[i++];
}
else
{
res[k++]=q[j++];
}
}
while(i<=mid) res[k++]=q[i++];
while(j<=r) res[k++]=q[j++];
//把剩下的那一段放到res里面去
Ac Code:
#include <iostream>
using namespace std;
const int N=100000+10;
int n;
int q[N];
int res[N];//最后的结果
void msort(int q[],int l,int r)
{
if(l>=r) return ;//当两个指针重合的时候就不用再排了
int mid=(l+r)/2;//分界点是中间
msort(q,l,mid);//排序左半边
msort(q,mid+1,r);//排序右半边
int k=0;
int i=l,j=mid+1;//两个指针分别指向左半边和右半边的开头
while(i<=mid && j<=r)
{
if(q[i]<=q[j])
{
res[k++]=q[i++];
}
else
{
res[k++]=q[j++];
}
}//合二为一(归并)
while(i<=mid) res[k++]=q[i++];
while(j<=r) res[k++]=q[j++];
//把剩下的那一段放到res里面去
i=l,k=0;//再分别指向q和res的开头位置
while(i<=r)
{
q[i]=res[k];//再把临时的res放回最后的q里面去
i++,k++;
}
}
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%d",&q[i]);
}
//输入
msort(q,0,n-1);
for(int i=0;i<n;i++)
{
printf("%d ",q[i]);
}
//输入
return 0;
}