The new ITone 6 has been released recently and George got really keen to buy it. Unfortunately, he didn’t have enough money, so George was going to work as a programmer. Now he faced the following problem at the work.
Given a sequence of n integers p1, p2, …, pn. You are to choose k pairs of integers:
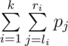 is maximal possible. Help George to cope with the task.
is maximal possible. Help George to cope with the task.Input
The first line contains three integers n, m and k (1 ≤ (m × k) ≤ n ≤ 5000). The second line contains n integers p1, p2, …, pn (0 ≤ pi ≤ 109).
Output
Print an integer in a single line — the maximum possible value of sum.
Sample test(s)
input
output
input
output
|
1
|
61
|
题目要求在$n$个数中选择$m$组长度为$k$的子序列使得和最大。
很容易想到,设 $f[i][j]$ 表示选择了i组,并且最后一组以j结尾的最大值。
那么 $large f[i][j]= max_{pleq j-k+1} left ( f[i-1][p] + sum[i]-sum[i-k] ight )$。
这显然是$O(N^3)$的过不了。
所以用$g[p]$表示$f[i-1][1 ightarrow p]$的最大值。
这样就可以$O(1)$转移了。
#include <iostream> #include <cstdio> #include <algorithm> #include <cstring> using namespace std; #define reg register inline char gc() { static const int BS = 1 << 22; static unsigned char Buf[BS], *st, *ed; if (st == ed) ed = Buf + fread(st = Buf, 1, BS, stdin); return st == ed ? EOF : *st++; } #define gc getchar inline int read() { int res=0;char ch=getchar();bool fu=0; while(!isdigit(ch)) {if(ch=='-')fu=1;ch=getchar();} while(isdigit(ch))res=(res<<3)+(res<<1)+(ch^48), ch=getchar(); return fu?-res:res; } #define ll long long int n, m, k; ll f[5005][5005], g[5005]; ll sum[5005]; ll ans; int main() { n = read(), k = read(), m = read(); for (reg int i = 1 ; i <= n ; i ++) sum[i] = sum[i-1] + read(); for (reg int i = k ; i <= n ; i ++) f[1][i] = sum[i] - sum[i-k], g[i] = max(g[i-1], f[1][i]); for (reg int i = 2 ; i <= m ; i ++) { for (reg int j = k ; j <= n ; j ++) f[i][j] = g[j-k] + sum[j] - sum[j-k]; memset(g, 0, sizeof g); for (reg int j = 1 ; j <= n ; j ++) g[j] = max(g[j-1], f[i][j]); } for (reg int i = k ; i <= n ; i ++) ans = max(ans, f[m][i]); cout << ans << endl; return 0; }