Peppa the Pig was walking and walked into the forest. What a strange coincidence! The forest has the shape of a rectangle, consisting of nrows and m columns. We enumerate the rows of the rectangle from top to bottom with numbers from 1 to n, and the columns — from left to right with numbers from 1 to m. Let's denote the cell at the intersection of the r-th row and the c-th column as (r, c).
Initially the pig stands in cell (1, 1), and in the end she wants to be in cell (n, m). Since the pig is in a hurry to get home, she can go from cell (r, c), only to either cell (r + 1, c) or (r, c + 1). She cannot leave the forest.
The forest, where the pig is, is very unusual. Some cells of the forest similar to each other, and some look very different. Peppa enjoys taking pictures and at every step she takes a picture of the cell where she is now. The path through the forest is considered to be beautiful if photographs taken on her way, can be viewed in both forward and in reverse order, showing the same sequence of photos. More formally, the line formed by the cells in order of visiting should be a palindrome (you can read a formal definition of a palindrome in the previous problem).
Count the number of beautiful paths from cell (1, 1) to cell (n, m). Since this number can be very large, determine the remainder after dividing it by 109 + 7.
The first line contains two integers n, m (1 ≤ n, m ≤ 500) — the height and width of the field.
Each of the following n lines contains m lowercase English letters identifying the types of cells of the forest. Identical cells are represented by identical letters, different cells are represented by different letters.
Print a single integer — the number of beautiful paths modulo 109 + 7.
3 4 aaab baaa abba
3
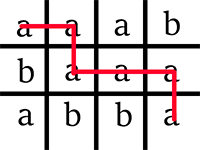
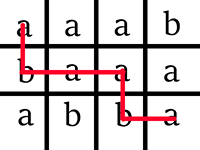
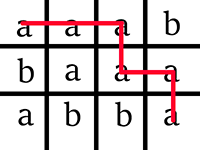
Picture illustrating possibilities for the sample test.
还是上英文题面霸气,。。。
这题比赛的时候根本没想到要dp
亏之前还写过那道 传纸条
太弱了啊。。。。
会发现满足回文即从前面走过来的和后面去的那个相同
注意回文分一下奇偶
所以想到f[i][j][p][q]表示前面走到(i,j)后面走到(p,q)
当且仅当map(i,j)==map(p,q)时可以向后面转移
会发现一共只需走n+m-1步
并且当(i,j)走过n+m-1的一半(走在刚好一半的时候仍可以)continue;
当两点汇合时统计ans
然后由于前面后面走的步数相同
所以根据i,j,q可以推出p
所以去掉p一维
然后假设某个状态是p+1或者p-1之类的
就把p的表达式里面的某个值做变化,使p变化就行了
可以用滚动数组优化
注意滚动的时候要memset!!!
刚开始还T了几个点
后来把dp数组开成int就AC了
longlong卡常数啊!!!
#include<cstdio>
#include<cstring>
char map[510][501];
const int mod=1e9+7;
int f[2][502][502];
inline bool judge(int x1,int y1,int x2,int y2)
{
if(x1==x2&&y1==y2)
return true;
if(x1+1==x2&&y1==y2)
return true;
if(x1==x2&&y1+1==y2)
return true;
return false;
}
int main()
{
int n,m;
scanf("%d %d",&n,&m);
char t;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
t=getchar();
while(t==' '||t=='
') t=getchar();
map[i][j]=t;
}
if(map[1][1]==map[n][m]) f[1][1][n]=1;
int ans=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
for(int p=n;p>=1;p--)
{
if(i+j-1>n+m-i-j+1) continue;
int q=n+m-p-i-j+2;
if(map[i][j]==map[p][q])
{
f[i&1][j][p]=(f[i&1][j][p]+f[(i-1)&1][j][p+1])%mod;
f[i&1][j][p]=(f[i&1][j][p]+f[(i-1)&1][j][p])%mod;
f[i&1][j][p]=(f[i&1][j][p]+f[i&1][j-1][p+1])%mod;
f[i&1][j][p]=(f[i&1][j][p]+f[i&1][j-1][p])%mod;
if(judge(i,j,p,q)) ans=(ans+f[i&1][j][p])%mod;
}
}
memset(f[(i-1)&1],0,sizeof(f[(i-1)&1]));
}
printf("%d
",(int)ans);
return 0;
}