【题解】洛谷P1073 [NOIP2009TG] 最优贸易（SPFA+分层图）

次元传送门：洛谷P1073

思路

一开始看题目嗅出了强连通分量的气息 但是嫌长没打 听机房做过的dalao说可以用分层图 从来没用过 就参考题解了解一下

因为每个城市可以走好几次 所以说我们可以在图上随意走动

所以第一层图就建一个边权为0的图 随意走动不影响

考虑在某个点买入水晶球

建立一条有向边到新图上 边权为-w[i] 指向i所能到达的点（第二层图中）

它表示：假如我选择走了这条边，就是我在这个点买了这个水晶球，我不会反悔，并且我接下来考虑在某个点卖它。

考虑在某个点卖出水晶球

从第二层图建立一条有向边到新图中 边权为w[i] 指向i所能到达的点（第三层图中）

它表示：假如我选择走了这条边，就是我在这个点卖了这个水晶球，我不会反悔，并且我接下来考虑走向终点。

现在我们只需要从第一层图走到第二层图再走到第三层图再走到终点即可 而且分层图把所有情况考虑到了

走向终点有两种情况

• 不买卖直接走向终点 在第一层图的终点连一条有向边 边权为0 到最后终点
• 要买卖再走向终点 在第三层图的终点连一条有向边 边权为0 到最后终点

由于有向边的建立，你不能从第二/三层走回第一层图，这保证了你只做一次买卖，而不是无限做买卖，符合了题目的要求（分层图的意义）

而我们最终的答案 就是求从第一层图的1号点 经过三层图走到“最后终点”的最长路

来自你谷dalao的图解：

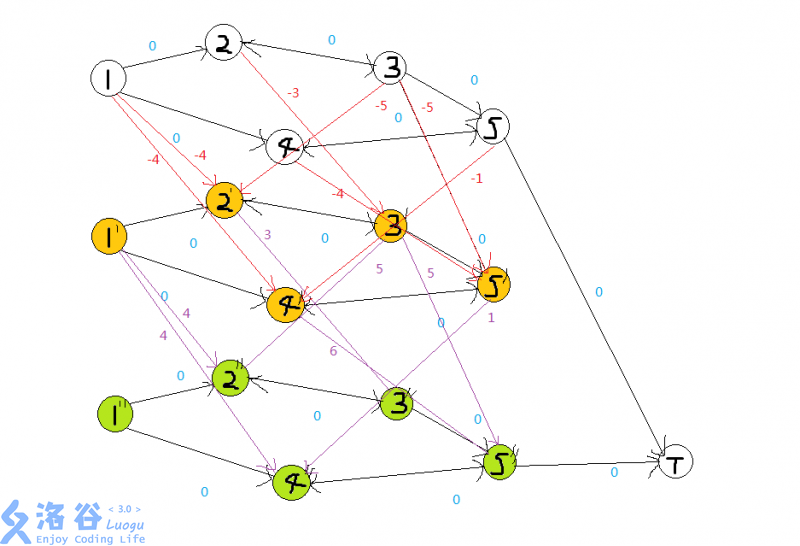
代码

#include<iostream>
#include<vector>
#include<queue>
using namespace std;
#define maxn 100010
#define INF 1e9+7
struct Edge
{
    int v;
    int len;
};
int n,m;
bool vis[maxn*3+1];
int w[maxn],dis[maxn*3+1];
vector <Edge> G[maxn*3+1];
void spfa()//常规SPFA 
{
     for(int i=1;i<=n;i++) dis[i]=-INF;
    queue <int> q;
    q.push(1);
    dis[1]=0;
    vis[1]=1;
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        vis[u]=0;
        for(int i=0;i<G[u].size();i++)
        {
            Edge x=G[u][i];
            if(dis[x.v]<dis[u]+x.len)
            {
                dis[x.v]=dis[u]+x.len;
                if(!vis[x.v])
                {
                    vis[x.v]=1;
                    q.push(x.v);
                }
            }
        }
    }
}
void add(int u,int v)
{
    G[u].push_back((Edge){v,0});//第一层 
    G[n+u].push_back((Edge){n+v,0});//第二层 用n+1到2*n 
    G[2*n+u].push_back((Edge){2*n+v,0});//第三层 用2*n+1到3*n 
    G[u].push_back((Edge){n+v,-w[u]});//从第一层到第二层 
    G[u+n].push_back((Edge){2*n+v,w[u]});//从第二层到第三层 
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>w[i];
    for(int i=1;i<=m;i++)
    {
        int x,y,z;
        cin>>x>>y>>z;
        add(x,y);
        if(z==2) add(y,x);
    }
    G[n].push_back((Edge){3*n+1,0});//第一层终点到最后终点 
    G[3*n].push_back((Edge){3*n+1,0});//第三层终点到最后终点 
    n=3*n+1;//更改最后终点 
    spfa();
    cout<<dis[n];
}