1.1 等价类划分法
1.1.1 测试中的疑问?
- 做加法器功能测试时,测试了1+1,1+2,1+3和1+4之后,还有必要测试1+5和1+6吗,能否放心地认为它们是正确的?
1.1.2 等价类划分
1) 把程序的输入域划分成若干部分,然后从每个部分中选取少数代表性数据作为测试用例
2) 每类的代表性 数据在测试中的作用等价于这一类中的其他值,如果某一 类中的一个例子发现了错误,这一 等价类中的其他例子也能发现同样的错误。反之,如果某-类中的一个例子没有发现错误,则这一类中的其他例子也不会查出错误
1.1.3 基础步骤
(一) 划分等价类和列出等价类表
- 有效等价类
- 无效等价类
- 确定等价类的原则
l 在输入条件规定了取值范围或值的个数的情况下,可以确立一个有效等价类和两个无效等价类。
l 在输入条件规定了输入值的集合或者规定了“必须如何"的条件的情况下,可以确立一个有效等价类和一个无效等价类。
l 在输入条件是一个布尔量的情况下,可确定一个有效等价类和一个无效等价类。
l 在规定了输入数据的一组值(假定n个) ,并且程序要对每一个输入值分别处理的情况下 ,可确立n个有效等价类和一个无效等价类。
l 在规定了输入数据必须遵守的规则的情况下,可确立一个有效等价类(符合规则)和若干个无效等价类(从不同角度违反规则)。
l 在确知己划分的等价类中,各元素在程序处理中的方式不同的情况下,则应再将该等价类进一步地划分为更小的等价类。
1.1.4 确定测试用例
1) 为每一个等价类规划一个惟一的编号
2) 设计一个新的测试用例,使其尽可能多覆盖尚未覆盖的有效等价类。重复这一步,最后使得所有有效等价类均被测试用例所覆盖
3) 设计一个新的测试用例,使其只覆盖一个无效等价类。重复这一步使所有无效等价类均被覆盖
1.2 边界值分析法
1.2.1 边界值得选择原则
1) 如果输入条件规定了值的范围,则应取刚达到这个范围的边界的值,以及刚刚超越这个范围边界的值作为测试输入数据。
2) 如果输入条件规定了值的个数,则用最大个数、最小个数、比最小个数少1、比最大个数多1的数作为测试数据。
3) 如果程序的规格说明给出的输入域或输出域是有序集合 ,则应选取集合的第一个元素和最后一 个元素作为测试用例。
4) 如果程序中使用了个内部数据结构 ,则应当选择这 个内部数据结构边界上的值作为测试用例。
5) 分析规格说明,找出其他可能的边界条件。
1.3 因果图法
1.3.1 李因果图法的来源
l 如考虑所输入条件之间的相互组合 ,会由于组合情况数目相当大,需要大量的测试用例
1.3.2 因果图法的特点
- 考虑输入条件间的组合关系
- 考虑输出条件对输入条件的信赖关系,即因果关系
- 测试用例发现错误的效率高
- 能检查出功能说明中的某些不一致或遗漏
- 因果图方法最终生产的就是判定表,它适合于检查程序输入条件和各种组合情况
1.3.3 因果图法基本步骤
1.3.3.1 根据功能说明书中规定的原因原因和结果之间的关系画图

1.3.3.2 识别出"原因"和"结果” ,并加以编号
案例: 有一个饮料自动售货机(处理单价为5角钱)的控制处理软件,它的软件规格说明如下。若投入5角钱的硬币,按下"橙汁”或"啤酒"的按钮,则相应的饮料就送出来。若投入1元钱的硬币,同样也是按"橙汁"或“啤酒"的按钮,则自动售货机在送出相应饮料的同时退回5角钱的硬币。

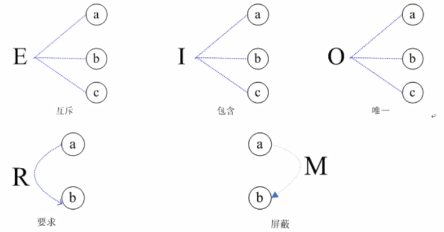
1.3.3.3 其中互斥、包含、唯一、要求时对原因的约束,屏蔽是对结果的约束。他们的含义如下
- 互斥:表示不同时为1,即a, b,c中至多只有一个1
- 包含:表示至少有一个1 , 即a,b , c中不同时为0
- 唯一:表示a,b , c中有且仅有一个1
- 要求:表示若a=1,则b必须为1.即不可能a= 1且b=0
- 屏蔽:表示若a=1 ,则b必须为0
1.4 判定表驱动法
- 心条件桩( Condition Stub ) :列出了问题得所有条件。通常认为列出的条件的次序无关紧要。
- 心动作桩( Action Stub ) :列出了问题规定可能采取的操作。这些操作的排列顺序没有约束。
- 心条件项( Condition Entry ) :列出针对它左列条件的取值。在所有可能情况下的真假值。
- 学动作项( Action Entry ) :列出在条件项的各种取值情况下应该采取的动作。
1.4.1 建立判定表的步骤
- 确定规则的个数
l 假如有n个条件,每个条件有两个取值(0 , 1) ,故有2n种规则
- 列出所有的条件桩和动作桩填入条件项
- 填入动作项,制定初始判定表
- 简化,合并相似规则或者相同动作
1.4.2 适合使用判定表设计测试用例的条件:
- 规格说明以判定表的形式给出,或很容易转换成判定表
- 条件的排列顺序不影响执行哪些操作
- 规则的排列顺序不影响执行哪些操作
- 当某一规则的条件已经满足,并确定要执行的操作后,不必检验别的规则
- 当某一规则的条件已经满足,并确定要执行的操作后,不必检验别的规则