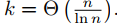《算法导论》第三章 练习题 Exercise

3.1-1

---

　　

　　假设存在 h(n) = Θ(f(n)+g(n)) ，由渐进符号 Θ 的性质知存在三个正常量c1、 c2、n₀，当n ≥ n₀时，使得 c1·(f(n)+g(n)) ≤ h(n) ≤  c2·(f(n)+g(n))，当 h(n) = max(f(n), h(n)) 时，令 c1 = 0.5，此时 max((f(n)+g(n))) > 0.5×(f(n)+g(n))； 令c2 = 1 ，有 max((f(n)+g(n))) < 1×(f(n)+g(n)) 。所以有 c1·(f(n)+g(n)) ≤ h(n) ≤  c2·(f(n)+g(n)) 成立。

3.1-2

---

　　

　　等价于证明 c1、c2为正常量，n₀ ≥ n 时，c1·n^b ≤ (n+a)^b  ≤ c2·n^b 成立。

　　由定理 3.1 知，我们应该从渐进上界和渐进下界来证明渐进确界。所以我们即要证明上式的左半部分也要证明上式的右半部分。

　　令 c2 = 2^b，当 n₀ 足够大( n₀ ≥ 2|a| )时，对于所有的 n ≥ n₀，有 (n+a)^b  ≤ (2n)^b = c·n^b成立。所以 (n+a)^b  = O(n^b)

　　令 c1 = 0.5，当 n₀ 足够大( n₀ ≥ 2|a| )时_，对于所有 n ≥ n₀，有 c·n^b = 0.5·n^b ≤ (n+a)^b 成立。所以 (n+a)^b  = Ω(n^b)

　　所以 (n+a)^b  = Θ(n^b)

3.1-3

---

　　

　　由渐进符号 O 的性质知，它是表示一个函数f(n)的上界，通俗地说就是表示增长率小于等于 n^2 的一些函数。而 “一个算法的运行时间至少是 O(n^2)” 表示运行时间函数 T(n) 取的是 f(n) 上方直到上界的区域，显然 O(1)等等的函数很可能也在这个区域里面，而T(n) 比 O(1) 增长率快并没有什么卵用。所以这种说法是没有意义的。

3.1-4

---

　　成立。令 c >= 2 即可。

　　不成立。找不到一个正常量 c，当 n足够大时，还可以保持 c >= 2ⁿ 。

　　

3.1-5

---

　　

　　充分性：令 f(n) = Θ(g(n))，则 存在三个正常量c1、 c2、n₀，当n ≥ n₀时，使得 c1·g(n) ≤ f(n) ≤  c2·g(n)，对于 c1·g(n) ≤ f(n)，有 f(n) = Ω(g(n));对于 f(n) ≤  c2·g(n)，有 f(n) = O(g(n))。

　　必要性：存在 c1 > 0、n₀ > 0，当n ≥ n₀时，使得 c1·g(n) ≤ f(n)；存在 c1 > 0、n₂ > 0，当n ≥ n₂时，使得 f(n) ≤  c2·g(n) 。取 max(n₀, n₂) ，有存在 c1>0、c2>0，当 n ≥  max(n₀, n₂) 时，c1·g(n) ≤ f(n) ≤  c2·g(n) 成立

3.1-6

---

　　

　　充分性：利用定理3.1，可以知道如果一个算法的运行时间是 Θ(g(n))，那么存在 c2 > 0，只要 n > n₀，不论你输入的 n 为何值，运行时间都会小等于 c2·g(n)，此时包含了最坏情况的运行时间；再次利用定理3.1，可以知道如果一个算法的运行时间是 Θ(g(n))，那么存在 c1 > 0，只要 n > n0，不管你输入的 n 为何值，运行时间都会大等于 c1·g(n)，此时包含了最好情况的运行时间。

　　必要性：如果在一个算法中，任何输入的运行时间都在最坏情况与最好情况的运行时间之间，那么可知它既是 O(g(n))，又是 Ω(g(n))，这儿的”是“相当于”∈“。由定理 3.1 知，它是 Θ(g(n))

3.1-7

---

　　

　　由于 ω(g(n)) = {f(n) | 对任意 c > 0，存在 n₀ >0, 使得 n > n₀ 时有 0 ≤ c·g(n) < f(n)} ，它表示的是非渐进紧确的下界。现在令f(n) = ω(g(n)) ，则 f(n) ∩ g(n) = φ ，所以 ο( f(n) ∩ g(n) ) = φ

　　或者利用反证法，假设 f(n) ∈ o(g(n)) ∩ ω(g(n))，则出现如下情况：

　　　　

　　矛盾。所以原命题不成立。

3.1-8

---

　　

　　Ω(g(n, m)) = {f(n, m) | 存在 c > 0、n0 > 0、m0 > 0，使得对所有 n ≥ n0 或 m ≥ m0，有 0 ≤ c·g(n,m) ≤ f(n, m)}

　　Θ(g(n, m)) = {f(n,m) | 存在 c1 > 0、c2 > 0、n0 > 0、m0 > 0，使得对所有 n ≥ n0 或 m ≥ m0，有 c1·g(n,m) ≤ f(n, m) ≤ c2·g(n,m)}

　　这儿的函数都是渐进非负的。

3.2-1

---

　　

　　已知对于 m <= n 时，f(m) <= f(n) ，g(m) <= g(n ) ，则由两函数相加，有 f(m) + g(m) <= f(n) + g(n) ，所以函数 f(n) + g(n) 是单调递增的。

　　令 a = g(m)， b = g(n) ，由于 g(n) 是单调递增的，则对于 a <= b，有f(a) <= f(b) 恒成立，所以 f(g(n)) 是单调递增的。

3.2-2

---

　　a^log_bc = a · (log_ac / log_ab) = c / log_ab = c · log_ba

3.2-3

---

　　

　　我们用 stirling 公式将 lg(!n) 化简，有下式：

　　

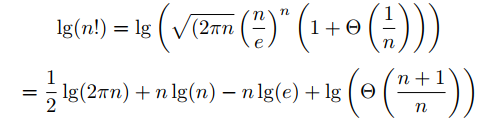
　　将最后一项化成对数相减的形式，发现这两项是近似相等的，可以消去，则式子主要受 n·_lg(n) 的影响，所以 _lg(n!) = _lg(n·_lg(n))

　　若证明 n! = _ω(2ⁿ) ，可以令 f(n) = n!，g(n) = 2ⁿ，求 n 趋于无穷时 g(n)/f(n) 的极限，即

　　

　　让 n >= 4e，右式 = 0。所以证明成立。

　　若想证明 n! = o(nⁿ)，同理，令 g(n) = nⁿ，f(n) = n!，求 n 趋于无穷时 g(n)/f(n) 的极限为无穷即可。有

　　

3.2-4 

---

　　

　　多项式有界就是指存在常量 k ，使得　f(n) = O(n^k) 成立。可以把这个等式两边取对数，有 _lgf(n) ≤ _lgc + k·_lgn ，所以只要满足 _lgf(n) = O(_lgn) ，则称 f(n) 是多项式有界的。

　　对于函数 f(n) = ⌈_lgn⌉ ! ，有 _lgf(n) = _lg(⌈_lgn⌉!) = Θ(⌈_lgn⌉·_lg⌈_lgn⌉) > O(_lgn)   ，所以

⌈_lgn⌉ ! 不是多项式有界。

　　对于函数 f(n) = ⌈_lg(_lgn)⌉ ! ，令 m = _lg(_lgn) ，有 _lgf(n) = _lg(m!) = Θ(m·_lgm) = Θ(_lg(_lgn)·_lg(_lg(_lgn))) = O(_lg(_lgn)·_lg(_lgn)) = O(_lgn) ，所以函数 f(n) =  ⌈_lg(_lgn)⌉ ! 是多项式有界

3.2-5

---

　　根据迭代对数的性质:　

　　可知 lg*n 是一个增长很慢的函数，比对数函数都慢。

　　记 n = 2ⁿ，则 lg* 2ⁿ = 1 +  lg* (lg 2ⁿ) ，有如下推导：

　　

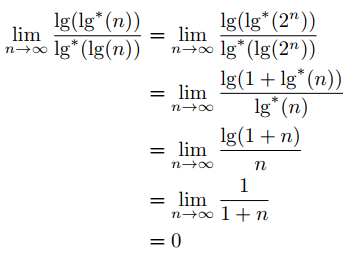
　　所以第二种增长的要更快。

3.2-6

---

　　

　　 

　　　　

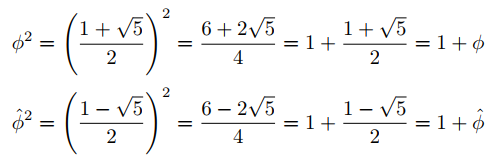
3.2-7

---

　　当 i = 0 时，  ；

　　当 i = 1 时，  ；

　　假设当 i = i - 1 时，  成立；

　　当 i  = i 时，  ；

　　证毕。

3.2-8

---

  

　　设存在 c1、c2 使得 c1·n ≤ k·_lnk ≤ c2·n 。

　　对 （ c1·n ≤ k·_lnk ）两边取对数，则有 _lnc1 + _lnn ≤ _lnk + _ln(_lnk) ，得 _lnn = O(_lnk) 。设存在 c3 使得   _lnn ≤ c3·_lnk ，则有  ，所以 

　　同理对 （ k·_lnk ≤ c2·n）进行相同的推导，有  ，所以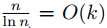 

　　由定理3.1 知，

　　由于 Θ 的对称性，得