[NOI2020] 超现实树

一、题目

点此看题

二、解法

首先要简化问题，我一开始就是直接想怎么合并然后两个小时没有结果，虽然已经摸到了正解的门槛 (...)

就想一下哪些树可能有用吧！如果直接考虑所有树的话太难了，可以大概感觉到最基本的树应该是一条链上面挂了叶子，这种结构我们称之为链树，链树是能生成许多树的状态的，但是是否有非链树的组合达到链树效果的情况呢？画下图呗：

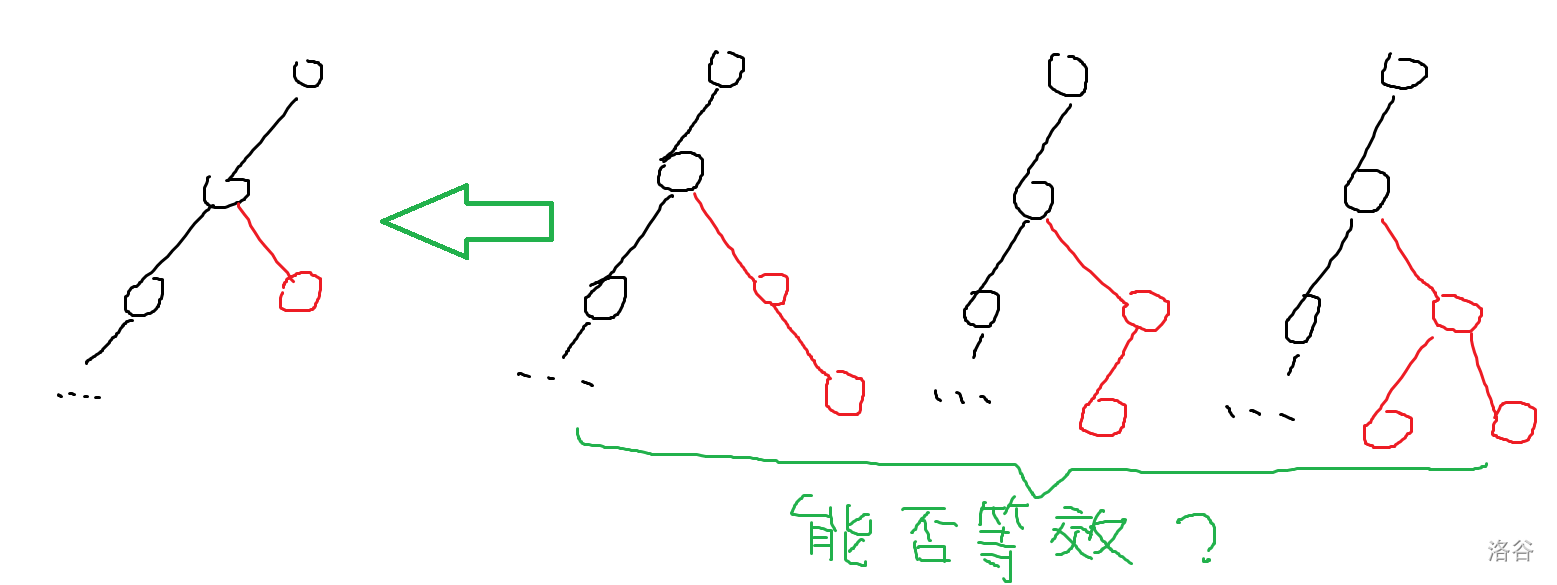
你仔细观察下就知道是不能等效的，因为链树只伸出去的叶子的情况会有无限多种，而这种情况在右边是没有的。所以说明了一个至关重要的结论：链树可以是生成无限树的基本树，并且非链树就算组合也不能等效链树

那么可以抛弃掉非链树了，只考虑链树问题会简化很多。现在我们要考虑很多链树的并集，可以考虑用某种状态表示链树，使得合并之后的状态能够等效合并前两个链树状态的并集，状态不会很多，从链树的形态出发分类：

• 状态 (1)：只有左儿子
• 状态 (2)：只有右儿子
• 状态 (3)：有右儿子，左儿子是叶子
• 状态 (4)：有左儿子，右儿子是叶子

那么可以把链树分类递归下去（每一个点都有一个状态），那么怎么定义状态是否合法呢？我们先固定上面递归下来的形态，在此基础上能生成无限多种树，由于我们定义的状态覆盖了所有情况，所以可以得到合法判定条件：

• 这个状态对应点是叶子（可能不同数对应不同点，只要有其一是叶子即可）
• 这个状态的四个子状态都合法

那么类似线段树合并写一下就行了，时间复杂度 (O(sum n))

总结一下，本题主要用到的思想是：简化问题（这一点很重要我没想到）；合并思想、等效思想（把一堆东西的组合等效单个东西）；定义状态（其实就找到了递归子问题）

#include <cstdio>
const int M = 2000005;
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int T,n,m,rt,cnt,ch[M][4],c[M],ls[M],rs[M];
int chk(int x)//判断是否是叶子 
{
	return !ls[x]&&!rs[x];
}
int pd(int x)
{
	if(chk(x) || (!rs[x] && pd(ls[x])) || (!ls[x] && pd(rs[x])))
		return 1;
	return (chk(rs[x]) && pd(ls[x])) || (chk(ls[x]) && pd(rs[x]));
}
void merge(int &x,int y)
{
	if(!x) x=++cnt;
	if(chk(y))
	{
		c[x]=1;
		return ;
	}
	if(!rs[y]) merge(ch[x][0],ls[y]);
	if(!ls[y]) merge(ch[x][1],rs[y]);
	if(ls[y] && rs[y] && chk(ls[y])) merge(ch[x][2],rs[y]);
	if(ls[y] && rs[y] && chk(rs[y])) merge(ch[x][3],ls[y]);
}
int grow(int x)
{
	if(!x||c[x]) return x>0;
	return grow(ch[x][0]) && grow(ch[x][1])
	&& grow(ch[x][2]) && grow(ch[x][3]);
}
signed main()
{
	T=read();
	while(T--)
	{
		m=read();
		cnt=rt=0;
		while(m--)
		{
			n=read();
			for(int i=1;i<=n;i++)
				ls[i]=read(),rs[i]=read();
			if(pd(1)) merge(rt,1);
		}
		if(grow(rt)) puts("Almost Complete");
		else puts("No");
		for(int i=1;i<=cnt;i++)
			for(int j=0;j<4;j++)
				ch[i][j]=c[i]=0;
	}
}