

”你这软件的用户需求有四百多项,
你难道就没意识到没有哪个人可以用这么复杂的产品么?”
”你说的很对,我最好在需求中再加一项——‘容易使用’。”
迪尔伯特系列漫画
作者:Scott Adams
当我第一次尝试学习机器学习算法时,我发现理解一个算法在干什么真的非常难。不仅仅是因为算法里各种繁杂的数学理论和难懂的符号,没有实际的例子,光靠定义和推导来了解一个算法实在是很无聊 。就连在我上网去查找相关的指导材料时,能找到的通常都是各种公式以及晦涩难懂的解释,很少有人能够细致的将所有细节加以说明。
直到有一个学数据科学的同学介绍我通过Excel表格来学习算法,我惊奇地发现这个方法很有效,我希望在此能够将它推广。具体方法呢,就是每当我学习一个新算法时,我都会在Excel里进行小规模 的实验。这种方法既能帮助你理解整个算法,又可以让你体会到这个算法的功能及奇妙之处。
下面让我举一个例子来给大家说明。大部分数据科学的算法都有关优化,其中最常用的一个就是梯度下降。这个例子是有关房价预测的:
现在,已知历史建筑数据(房屋大小及价格),我们的目的是对于未来某个特定面积大小的房屋,我们能够通过数学模型估算出此房屋的价格。举个例子,如果我未来想买一个100平方米的房子,大约要多少钱呢?我希望我们的模型能解决这个问题。

换而言之,用数学语言来表达我们的问题:对于一个新房子,已知它的面积(X), 求它的价格(Y)。
让我们先用折线图的形式把目前的房屋数据表达出来:
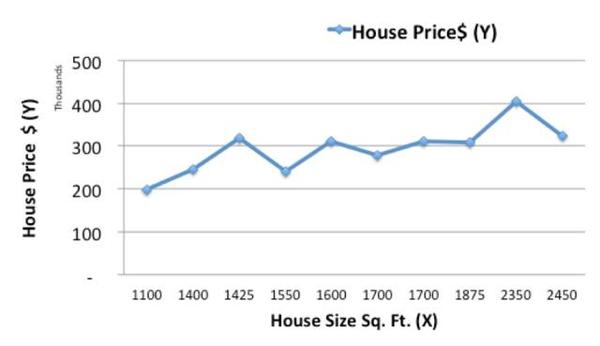
现在,我们就先用一个简单的线性模型,用一条直线来表明房价与房屋面积大小的关系。
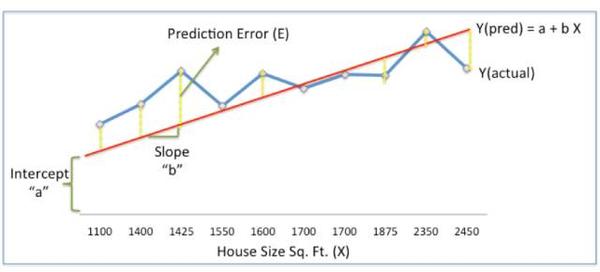 (Prediction error: 预测误差, intercept:截距, slope:斜率)
(Prediction error: 预测误差, intercept:截距, slope:斜率)
在以上的表格中,红线(Ypred)代表给定房屋面积(X)预测的房价。
Ypred = a + bx (线性公式)
蓝线代表目前真实房屋面积所对应的房价(Yactual)。黄色的虚线,代表着预测误差(E),也就是Yactual 和 Ypred的差值。所以,我们为了使误差(E)减小从而增加预测精准度,我们需要找到合适的a,b值(又称比重)来确定Ypred这条线。
因此我们模型的目的,就是要找出最佳的a,b值(又称比重),从而使Ypred这条线最均匀得穿过各个点,也就是使得误差(E)最小,从而最大化地提高预测精准度。
 (注意SSE只是测量误差的一种方式,另外有其他的方式本文暂且不表)
(注意SSE只是测量误差的一种方式,另外有其他的方式本文暂且不表)
现在我们的梯度下降法就派上用场了,梯度下降法这种优化算法可以帮我们找到最优的a,b值从而使得预测误差减小。
下面我们就一步一步地拆分梯度下降法:
-
第一步:随机将比重(a,b)赋值并计算误差平方和(SSE)
-
第二步:计算出梯度,即通过微调比重(a,b)从而改变差平方和(SSE)。这样做可以使得a,b值可以向SSE最小化的方向靠拢
-
第三步:用梯度调整a,b从而达到最优结果,即SSE最小
-
第四步:用新的a,b来做预测,即得到最优的Ypred(红线)并且计算新的SSE
-
第五步:重复三四步直到调整a,b不会明显的影响SSE
接下来,我们会用具体例子来解释这五步(接下来我会用 Excel展示)。但在此之前,我们需要使数据标准化从而使得优化过程更加快。
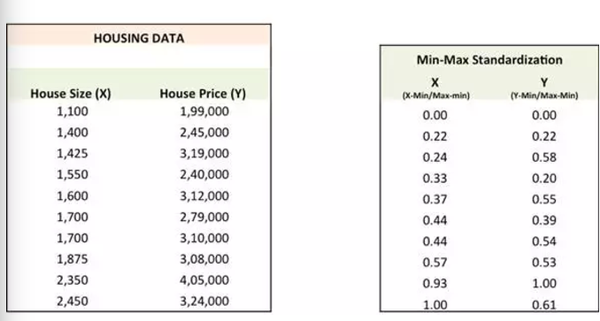
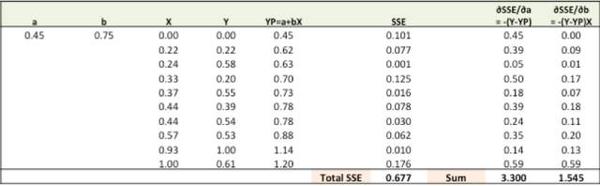
第一步:随机对比重(a,b)赋值并计算误差平方和(SSE)
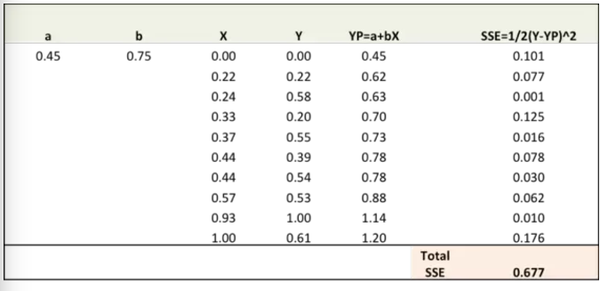
第二步:通过对误差比重(a,b)求导计算出误差梯度(注:YP即Ypred)
∂SSE/∂a = – (Y-YP)
∂SSE/∂b = – (Y-YP)X
误差公式:SSE=½ (Y-YP)^2 = ½(Y-(a+bX))^2
这里涉及到一些微积分,不过仅此而已。∂SSE/∂a 和 ∂SSE/∂b 就被称之为梯度,他们代表a,b相对SSE移动的方向。
第三步:通过梯度调整a,b,使得a,b最佳即所得SSE最小
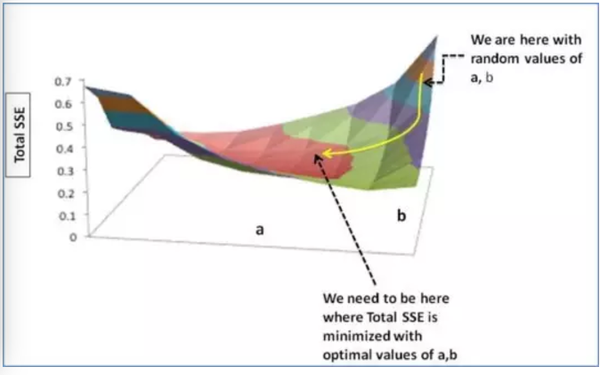
(右上角是我们随机的a,b所取得的SSE值,我们需要找到图中黑虚线所指的SSE最小值)
我们通过改变a,b来确保我们的SSE会向最小值方向移动,即沿黄线所指方向。至于改变a,b的规则:
-
a – ∂SSE/∂a
-
b – ∂SSE/∂b
所以,具体的公式就是:
-
New a = a – r * ∂SSE/∂a = 0.45 - 0.01 * 3.300 = 0.42
-
New b = b – r * ∂SSE/∂b = 0.75 - 0.01 * 1.545 = 0.73
在这里,r代表学习率 = 0.01,可以自设,是用来决定调整a,b快慢的。越大调整的越快,但越容易漏掉收敛的最佳点。
第四步:用新的a,b来求出新的SSE
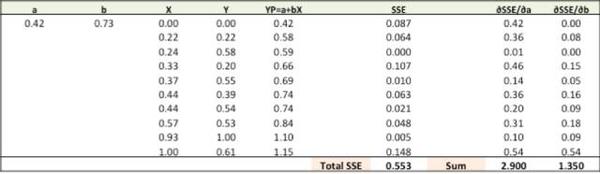
大家可以从图上看出,总的SSE值(Total SSE)从原来的0.677变为0.553。代表着我们的预测准度正在增加。
第五步:重复三四步直到调整a,b不会明显的影响SSE。到那时我们的预测准度就会达到最高
这就是梯度下降法,这个算法及他的变种是许多机器学习的算法,如神经式网络,深度学习的核心组成部分。
作者简介:Jahnavi Mahanta 是机器学习和深度学习的狂热爱好者,她在过去的十三年期间在American Express公司领导了多支机器学习的小组。她同时也是Deeplearningtrack的联合创始人,Deeplearningtrack是个在网上自主学习数据科学的网站,她也在此网站上担任讲员。
免责声明:
请注意本文只是教学文章,因此:
1. 所用的数据都非真实的,并且数据的量非常小。并且为了简化例子,我们用的数据和模型都只有一个变量。(生活中房价的高低不光与房屋面积的大小有关,还与地段及其他各种因素有关)
2. 本篇文章重点在于通过Excel来让读者更简单理解梯度下降这个算法的概念,所以本篇没涉及到梯度下降的优劣性,比如同最小二乘回归法(least square regression)的比较等等。
3. 因为数据量太小,所以本文中用所有的数据进行训练(training)。然而在实际生活中,我们也许会用到各种数据有效性(data validation)的方法。(比如—将数据分为训练集和测试集(training set/testing set)或者交叉验证(N—Cross Validation))