出处: http://blog.csdn.net/tangyongkang
转贴请注明出处
1 围绕原点的旋转
如下图, 在2维坐标上,有一点p(x, y) , 直线opの长度为r, 直线op和x轴的正向的夹角为a。 直线op围绕原点做逆时针方向b度的旋转,到达p’ (s,t) 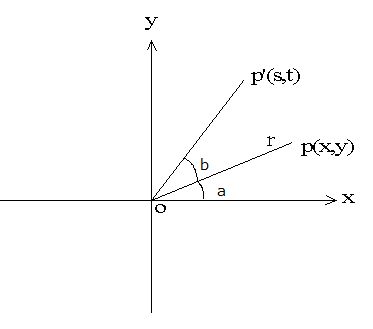
s = r cos(a + b) = r cos(a)cos(b) – r sin(a)sin(b) (1.1)
t = r sin(a + b) = r sin(a)cos(b) + r cos(a) sin(b) (1.2)
其中 x = r cos(a) , y = r sin(a)
代入(1.1), (1.2) ,
s = x cos(b) – y sin(b) (1.3)
t = x sin(b) + y cos(b) (1.4)
用行列式表达如下:
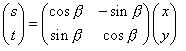
2.座标系的旋转
在原坐标系xoy中, 绕原点沿逆时针方向旋转theta度, 变成座标系 sot。
设有某点p,在原坐标系中的坐标为 (x, y), 旋转后的新坐标为(s, t)。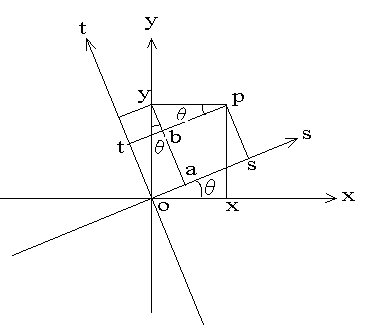
oa = y sin(theta) (2.1)
as = x cos(theta) (2.2)
综合(2.1),(2.2) 2式
s = os = oa + as = x cos(theta) + y sin(theta)
t = ot = ay – ab = y cos(theta) – x sin(theta)
用行列式表达如下:
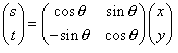
cos(a+b) = cos(a)*cos(b)-sin(a)*sin(b)的推导
附件: